A fast-running method for blast load prediction shielding by a protective barrier
2020-05-23SungChong
S.-H. Sung, J.-W. Chong
Agency for Defense Development, Yuseong P. O. Box 35, DaeJeon, 395-600, South Korea
Keywords:Blast loads Protective barrier Shock wave Fast running model Kingery-Bulmash
ABSTRACT This study presents a simplified blast load prediction method on structures behind a protective barrier.The proposed method is basically an empirical approach based on Kingery-Bulamsh(K-B)chart and finite element (FE) analysis results. To this end, this study divides the structure into three regions by three critical points. Blast loads at each critical point can be calculated based on K-B chart and an approximation according to FE analysis results. Finally, peak reflected overpressure and impulse distributed on the structure can be approximately estimated by linearly connecting blast loads at each critical point.In order to confirm a feasibility of the proposed method,a series of numerical simulations were carried out.The simulation results were compared with FE analysis results which are presented in the open literature.From such comparisons,it was found that the proposed method is applicable to predict blast loads on structures behind a protective barrier.
1. Introduction
Structural damages can be caused by terrorist attacks and accidental explosion events. In order to protect structures from such unexpected accidents, urban planners consider the construction of a protective barrier. The protective barrier can reduce blast loads acting on a structure by blocking direct blast wave propagation.Blast loads on structures behind a barrier can be influenced by various design parameters such as detonation points, barrier heights,the distance between structures and barriers,etc.In other words,it is necessary to determine an optimal barrier position and its optimal height to minimize structural damages by unexpected accidents.
An excellent review to predict or estimate blast loads on structures behind a protective barrier can be found in Refs. [1-3].Rose et al.[4,5]carried out scaled tests and developed contour plots of overpressure and impulse behind a blast wall. They also experimentally investigated an influence on the types of wall and concluded that non-permanent structures can provide a high degree of blast wave attenuation[6].Ngo et al.[7]conducted a series of FE analyses to confirm the effectiveness of barrier walls. Hajek and Foglar [8] numerically and experimentally investigated the effect of rigid barriers in the confined space.Hajek et al.[9]studied on the influence of barrier material and barrier shape on blast wave mitigation. Sochet et al. [10] focused on the dimensioning of protective barriers and showed the advantage of using a barrier with a vertical front or rear face.Schuldt and El-Rayes[11]developed Blast Effects Assessment Model (BEAM) capable of effectively quantifying and visualizing blast effects on a facility behind a protective barrier.Xiao et al.[12]investigated shock wave attenuation effects using protective barriers made of steel posts.
However,it is difficult to carry out a variety of experiments and finite element (FE) analyses since it takes a lot of time and cost.
For this reason, the development of fast running models to predict blast loads on structures behind a barrier has been highly needed. A neural-network approaches [13,14] have received considerable attention to reduce an overhead of hardware requirements.Eveillard[15]developed fast running method to define effects areas near protective barriers. As another alternative tool,Zhou and Hao [16] proposed approximate pseudo-analytical formulae based on the best-fit curve of numerical simulations.The derived formulae were presented in terms of the critical parameters such as explosive weights,the distance from explosives to the structure,total height of the structure,barrier heights,etc.This method used several critical points and modification factors to simplify peak overpressure and impulse distribution along the structural height.The approximate formulae provided a simple and reliable estimation of blast loading on structures behind a protective barrier.
This study proposes a simplified blast load prediction method on structures behind a protective barrier as another alternative fast running model. The proposed fast-running method can predict blast loads on structures behind a protective barrier in a few seconds, while FE method requires several hours or several days for the same numerical simulation case.The method uses the concept of critical point presented by Zhou and Hao[16].Each critical point is empirically estimated based on FE analysis results.Blast loads at each critical point can be calculated based on Kingery-Bulmash(KB)chart[17]and an approximation according to FE analysis results.Peak reflected overpressure and impulse distributed on the structure can be approximately estimated by linearly connecting blast loads at each critical point.
2. Theoretical background
2.1. Basic concept of the proposed method
Under the assumption that a protective barrier is rigid, this study predicts blast loads behind a protective barrier on structures based on the concept of critical point. The proposed method is identical to the previous method[16]in terms of using the concept of critical point, while procedures to determine critical points and to obtain blast loads at the points are different each other. This study divides regions of the structure behind a protective barrier by three critical points, as shown in Fig.1.
The point 1 separates regions that are influenced by the barrier and that are not. The region 1 is the part where blast loads are completely propagated without being disturbed by the barrier. On the other hand, other regions are disturbed by the barrier due to diffraction of show waves[18].The point 2 has the same height as the top of the barrier. In the region 2, the wave impinges either directly on the target structure or after one diffraction around the left corner of the barrier, and a ground-reflected wave gradually decreases along the structural height (See Fig.1). In the region 3,two diffractions occur around the both corner of the barrier,and a ground-reflected wave gradually increases along the point 2 to the point 3(See Fig.1).For this reason,the point 2 is determined as the critical point. The point 3 is the ground level of the structure.
2.2. Estimation of blast loads at critical points
2.2.1. Estimation of blast loads at the point 1
In this study, a comparative study with a variety of FE analysis results described in Ref. [16] was performed to determine an optimal position of the point 1. Thus, the optimal position was estimated by examining a point that minimizes thechanging the position of the point 1,as shown in Fig.2.Finally,the optimal position of the point 1 was determined to 1.9 times of He through the parametric study(See Fig.1 and Fig.2).If additional FE analysis results are obtained under various blast scenarios and barrier configurations,the optimal position of the point 1(1.9×HE)may be modified.

Peak reflected overpressure and impulse at the point 1 can be calculated based on K-B chart(See Fig.3)using an explosive weight(W)and a stand-off distance(d),since the region 1(See Fig.1)is the undisturbed region by the barrier.
2.2.2. Estimation of blast loads at the point 2
Blast loads at the point 2 can be simplified to the sum of an incident wave (Wave 1) and a ground-reflected wave(Wave 2), as depicted in Fig. 4. The Wave 1 can be calculated based on a diffraction coefficient. Miller [20] recommended the diffraction coefficient as 0.35 about a rectangular structure.Thus,information on the Wave 1 can be estimated based on K-B chart and the diffraction coefficient. (i.e., W: explosive weight,L1+L2: total stand-off distance, 0.35: diffraction coefficient).

Fig. 2. Estimation of the optimal position of the point 1.

Table 1 Simulation scenarios.
Next,this study assumes that the Area 1(See Fig.4)is the room having openings. Under this assumption, the simplified internal blast pressure model[21]can be used to obtain information on the Wave 2. In the fast-running method, since the simplified internal blast pressure model is applied to estimate the Wave 2 at the point 2,Mach stem effect cannot be considered.Thus,the Wave 1 and the Wave 2 can be considered as the first triangular wave and the second triangular wave in Fig. 5, respectively. On the other hand,the third triangular wave in Fig.5 can be neglected since this study only considers major two waves, as shown in Fig. 4. Under this assumption, since the pressure-time history at the point 2 can be estimated using the major two waves in Fig. 5, the peak reflected overpressure at the point 2 is same with the peak reflected overpressure of the Wave 1(Pr),and the total impulse at the point 2 can be determined to 1.5×Ir(i.e.,Ir+1/2 ×Ir).
2.2.3. Estimation of blast loads at the point 3
Blast loads at the point 3 can be empirically estimated similar to the previous method [16]. The method used a maximum value among the values of critical points.However,this study suggests to use the mean value of the point 1 and the point 2 instead of the maximum value,since the use of the mean value was more reliable for various simulation cases. When the maximum value was used,the MAD between FE analysis results[16]and the proposed method results was about 82.9 kPa.On the other hand,the MAD was about 41 kPa when the mean value of the point 1 and the point 2 was utilized.

Fig. 3. K-B chart [19]: (a) Free-air burst; (b) Surface burst.
The flow chart to evaluate peak reflected overpressure and impulse at each point on the structure is briefly summarized in Fig.6.
3. Numerical simulation

Fig. 5. Simplified internal blast pressure model [20].
Prior to perform numerical simulation, a preliminary comparative study was carried out to confirm an error between K-B chart and FE analysis.To this end,blast loads at target structure without protective barrier were estimated based on K-B chart. The target structure is a 20 m building,and blast loads acting on the structure was calculated with 1 m interval from the ground level,as depicted in Fig. 7. The explosive weight is 1,000 kg, and FE analysis results were used described in Ref.[16]for comparison.The results of the preliminary study are shown in Fig. 8. In Fig. 8, thex-axis values represent overpressures (or impulses) of FE analysis results normalized by maximum overpressure (or maximum impulse) of FE analysis results. They-axis values represent overpressures (or impulses)of K-B results normalized by maximum overpressure(or maximum impulse) of FE analysis results. For peak overpressure,the two simulation results coincided well each other.On the other hand, the maximum error was about 22.5%for impulse.
Numerical simulation was performed in the same scenarios as FE analysis described in Ref. [16]. AUTODYN3D was utilized in the previous study to carry out numerical analyses to predict pressuretime histories on structures behind a barrier. The simulation scenarios are shown in Table 1.
For Case #1, the procedure to obtain blast loading parameter based on the flow chart in Fig. 6 is depicted in Fig. 9.

Fig. 6. Flow chart to evaluate blast loads distributed on a structure.

Fig. 7. Preliminary simulation scenario.
Fig.10-Fig.12 show normalized peak reflected overpressure and normalized impulse distributed on the structure estimated from FE analysis and the proposed method for each scenario. For direct comparison with the open literature results [16], peak reflected overpressures and impulses normalized by peak reflected overpressure and impulse at the ground level evaluated from the no barrier case analysis were used. It was shown that peak reflected overpressures estimated from two different simulations coincided well each other. On the other hand, for impulse, it had a relatively large deviation compared to the peak reflected overpressure. This result is due to the difference between the impulse at the top of the structure calculated by K-B chart and the impulse at the top of the structure which is estimated from FE analysis,as shown in Fig.8.In other words,it is an inevitable error caused by the uncertainty of KB chart. The phenomenon also occurs in the method proposed by Zhou and Hao [16], if a large difference exists between blast loads estimated from FE analysis and other empirical methods at the ground level. This is a limitation of the empirical methods.
Fig.13 and Fig.14 represent the mean absolute deviation(MAD)for peak reflected overpressure and impulse between results by FE analysis and by the proposed method.


Fig. 8. Preliminary study results: Uncertainty estimation for K-B chart.

Fig. 9. Flow chart to evaluate blast loading parameters for Case #1.
whereis the blast loading parameter atj(m)height estimated from FE analysis, andKjis the blast loading parameter atj(m)height estimated from the proposed method,nis the number of measuring points along the height of the structure.
Here,the red line is the MAD for preliminary study results(i.e.,no barrier case). For peak reflected overpressure, the mean of the MADs is about 68.3 kPa.The value is about 1.57 times of that of the preliminary study.For impulse,the mean of the MADs is about 1.02 times as compared with the no barrier case.The error has increased in the simplification process based on the empirical formula about the complex physical phenomena such as diffraction and reflection of the blast waves due to a protective barrier.
Consequently, it was found that the proposed method can quickly predict the tendency of blast loads distributed on structures behind a protective barrier. However, it should be noted that the proposed fast-running method may induce relatively large errors compared to FE analysis results. This is a limitation of empirical formula-based fast-running methods.
4. Conclusion
In this study, a simplified blast load prediction method on structures behind a protective barrier was proposed.
· The method can empirically evaluate blast loads distributed on the structures based on K-B chart and an approximation in accordance with FE analysis results.
· The concept of critical point was used to quickly predict blast loads behind a protective barrier. Thus, the structure can be divided into three regions by three critical points, and information on each critical point can be calculated based on K-B chart and the approximation. Finally, blast loads distributed on the structure can be approximately evaluated by linearly connecting blast loads at each critical point.

Fig.10. Case #1~Case #4 (a) Normalized peak reflected overpressure distribution (b) Normalized impulse distribution. (·: by FE analysis, ○: by the proposed method).

Fig.11. Case #5~Case #8 (a) Normalized peak reflected overpressure distribution (b) Normalized impulse distribution (·: by FE analysis, ○: by the proposed method).
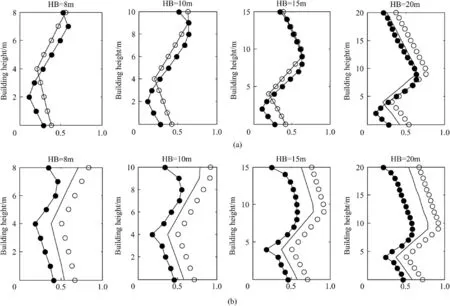
Fig.12. Case #9~Case #12 (a) Normalized peak reflected overpressure distribution (b) Normalized impulse distribution (·: by FE analysis, ○: by the proposed method).

Fig.13. Mean absolute deviation of peak reflected overpressure for each simulation(by FE analysis vs by the proposed method).
Peak reflected overpressure and impulse estimated from the proposed method were compared with FE analysis results described in the open literature.
· Peak reflected overpressure was reliably evaluated from the proposed method.
· On the other hand,in some cases,impulse had a relatively large error compared to the peak reflected overpressure.

Fig.14. Mean absolute deviation of impulse for each simulation (by FE analysis vs by the proposed method).
· This result is due to the deviation between the impulse at the top of the structure calculated by K-B chart and the impulse at the top of the structure, which is estimated from FE analysis.Thus, it is an inevitable error occurred in empirical methods.Nevertheless, mean absolute deviations of peak reflected overpressure and impulse were about 1.57 times and about 1.02 times,compared to no barrier case.
In conclusion, the proposed method can quickly predict the tendency of blast loads distributed on structures behind a protective barrier. However, it should be noted that the proposed fastrunning method may induce relatively large errors compared to FE analysis results. In other words, if sufficient time and a small number of analysis cases are given,it is advantageous to utilize the hydro-code such as Autodyn, LS-Dyna, etc. On the other hand, if a user wants to check the trends in various simulation cases for a short time, the proposed fast-running method can be used for a predictive approach.
Acknowledgement
The work was supported by the Agency for Defense Development.
杂志排行
Defence Technology的其它文章
- A comparison of the ballistic behaviour of conventionally sintered and additively manufactured alumina
- Effect of operating temperature on aged single lap bonded joints
- Investigation on energy output structure of explosives near-ground explosion
- Characteristics structure analysis on debris cloud in the hypervelocity impact of disk projectile on thin plate
- Coating processes towards selective laser sintering of energetic material composites
- Dynamic modeling and parameter identification of a gun saddle ring
