An INS/GNSS integrated navigation in GNSS denied environment using recurrent neural network

Hai-fa Dai, Hong-wei Bian, Rong-ying Wang, Heng Ma

Navigation Engineering Lab, Naval Engineering University, Wuhan, CO, 430033, China

Keywords:Inertial navigation system (INS)Global navigation satellite system (GNSS)Integrated navigation Recurrent neural network (RNN)

ABSTRACT In view of the failure of GNSS signals, this paper proposes an INS/GNSS integrated navigation method based on the recurrent neural network(RNN).This proposed method utilizes the calculation principle of INS and the memory function of the RNN to estimate the errors of the INS, thereby obtaining a continuous,reliable and high-precision navigation solution.The performance of the proposed method is firstly demonstrated using an INS/GNSS simulation environment. Subsequently, an experimental test on boat is also conducted to validate the performance of the method. The results show a promising application prospect for RNN in the field of positioning for INS/GNSS integrated navigation in the absence of GNSS signal, as it outperforms extreme learning machine (ELM) and EKF by approximately 30% and 60%, respectively.

1. Introduction

In order to assure the high precise,robust,reliable and continue navigation service for vehicle, the integrated navigation with inertial navigation system (INS) and Global navigation satellite system (GNSS) using extend Kalman filters (EKF) has been proposed for a number of years [1-3]. However, EKF still has some shortcomings.In the EKF method,an accurate knowledge of the random error model associated with the sensor used is required.For GNSS and INS subsystems,statistical properties such as correlation time,measurement noise covariance and dynamic noise covariance should be known accurately[4].In order to be able to use the EKF method,linearization of the vehicle dynamic model may reduce the estimation accuracy in consideration of highly nonlinear state errors. In addition, the linearization model of the error state in the EKF method is only effective for short-time GPS signal outage.These methods cannot be updated by GPS measurements in longterm GPS signal outage in urban environments or in conditions of navigational warfare and underwater [5,6].

To overcome the above-mentioned problems, many methods based on artificial neural network(ANN)which uses different kinds of neural network structures have been recently put forward in the field of INS/GPS integrated navigation. Early methods are mostly based on static networks that include muti-layer perception(MLP)[7]and radial basis function(RBF)[8,9].Where,the MLP technique has problems in real-time implementation [10]. The RBF network increases the training speed for real-time, but it can't mimic the dynamic model for the reason that it does not consider the error dependency on past INS information [11]. To solve this problem,input delayed neural networks (IDNN) were utilized to characteristic the INS position and velocity errors, which were based on current and past INS position and velocity information [12]. Dynamic neural networks are more reliable than static networks because they can be trained to learn the dynamic model varying with time [12]. Nevertheless, the major drawback of these networks is that the complexity and training time were increased greatly, and it needs the right NN architecture to match the error dynamics [11].

Adaptive neuro-fuzzy inference system(ANFIS)has an effective performance by combining the learning ability of DNN and the expert knowledge of fuzzy logic. ANFIS can deal with the imprecision,uncertainty and randomness of input data on the condition of nonlinear dynamic environments. As a result, ANFIS method is developed to operate in real time with GPS/INS integration[10,11].Nevertheless, there are some inadequacies about parameter optimization with the ANFIS methods,which leads to a huge amount of computation and long design time[1].Furthermore,some scholars propose methods based on ELM. The EML is a relatively new proposed feedforward neural network,which has only one hidden layer, and has a mechanism to automatically select parameters of hidden layer to obtain the output weights.

Fig.1. The network structure of RNN.

The above-mentioned ANN-based techniques have been developed greatly in this field. Nevertheless, it still has many shortcomings such as slow convergence and poor generalization performance. It may be contributed to the fact that these works didn't figure out the accurate relation between the other associated variables and the errors of INS position and velocity. On the other hand, they didn't relate the current error with past error. In this paper, an INS/GNSS integrated navigation using recurrent neural network(RNN)is proposed.RNN is a kind of time recursive neural network which has the function of memory and feedback, and it can predict current errors by integrating the last errors of position and velocity with change rate of velocity and attitude.

The subject matter of this paper is presented as follow.In section 2,the INS navigation calculation process is illustrated.Besides,the equations of position error and velocity error are formulated. In section 3, the structure and principle of RNN are introduced. In section 4,the general methodology of integrating INS/GNSS system is stated. This section presents a data fusion algorithm using RNN.Section 5 is devoted to the experimental tests.These experimental results of simulation environment and dynamic vehicle tests which applies the proposed estimation algorithm are shown and compared with the obtained experimental results based on the EKF and ELM methods. Finally, conclusion and suggestions of future research are given in section 6.

Fig. 2. The network expand structure of RNN in time.

2. Integrating vehicle dynamics

INS includes an inertial measurement unit (IMU) and a navigation processor.The IMU measures the vehicle's specific forceand angular velocityby accelerometers and gyroscope along the body frame. The b represents the body frame and i represents the inertial frame. They are integrated to obtain the velocity, position and attitude of the vehicle. However, the navigation state of the vehicle will diverge with time due to the influence of accelerometer and gyro bias.

If we use the direction cosine matrix to represent the vehicle's attitude, its differential equation is given as [13]:

Then the vehicle's attitude can be obtained by integrating Eq.(1)and assuming the angular velocity and is constant during integration period:

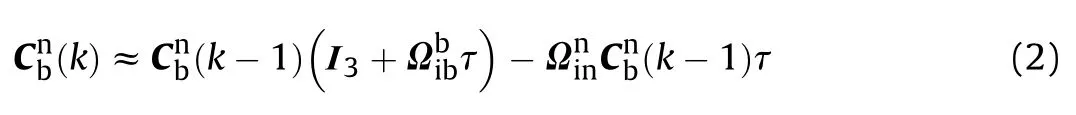
Where,krepresents thekth time step, I3is 3 by 3 unit matrix, τ denotes the integration period.

The velocity differential equation in local navigation coordinate system is given as:

Fig. 3. Train mode of INS/GNSS integrated system using RNN.

The position differential equation in NED coordinate system is given as:

Assume that the velocity varies linearly during the integration period and integrating Eq. (5) to obtain the position as:

Considering the influence of accelerometer and gyro bias, the actual measurement positionis:

The position error δpequals to:

Where, the subscripts and subscripts are omitted for ease of description.

Similarly, according to Eq (4) the calculated error of velocity δv can be written as:

Where, the effects of gravity deviation are ignored,is the measured vehicle's specific force,is the measured error of specific force,is the calculated attitude direction cosine matrix,is the attitude error matrix, and it is calculated as:

Substituting Eq. (9) into Eq. (8), get:

Fig. 4. Predict mode of INS/GNSS integrated system using RNN.

Fig. 5. Simulated trajectory.

According to Eq. (10) and Eq. (11), the current position error δp（k） relates last position error δp（k- 1）, last velocity error δv（k-1）,the angular velocitycurrent attitudeattitude error(related to), the measured special forceand its measured errorAll of these variables can be obtained by INS data directly except the measured error of special forceand angular velocity errorwhich will be analyzed as follow.

After calibration and compensation,the IMU measurements are modeled as:

Where,bais the bias of accelerometer,bgis the bias of gyro,waand wgare corresponding Gaussian process noise, respectively.

And then, the measurement error of accelerometer and gyro are:

For convenience, the bias can be divided into two parts: static component （bas，bgs） and dynamic component （bad，bgd）:

Fig.6. Reference positioning error and the RNN predicted position error in North(top),East (middle) and Down (bottom).

Where, the static component includes successively starting bias and remaining constant value items after calibration, which is always constant during the navigation. While the dynamic component varies with environment and vehicle's dynamic.

Fig. 7. Reference velocity error and the RNN predicted velocity error in North (top),East (middle) and Down (bottom).

In summary, the current position error relates to the INS data,last INS error, accelerometer static bias, static gyro bias, vehicle's dynamic and the environment.However,the relations between the position error and these factors are nonlinear and hard to be modeled. As a result, an AI technique based on recurrent neural network (RNN) is proposed in this paper to map these relations.

Fig. 8. Whole trajectory of sea trial.

3. Recurrent neural network

Recurrent neural network (RNN) is a kind of time recursive neural network, which was first proposed by Rumelhart et al., in 1986[14].Compared with common neural network,it has memory function to save the old information and can model the feature of time-varying system.

The network structure of RNN is shown in Fig.1.As can be seen,there are some links were added between the nodes in hidden layer compared with the ordinary neural network,such as convolutional neural network (CNN) and deep neural network (DNN). For the convenience of analysis, we expand the RNN network in time to obtain the structure which is shown in Fig.2.Where,xtdenotes the input at instantt,otdenotes the output at the same time,Fdenotes the activation function. As the picture shows, the last output was stored as the input of current neural network with current inputxt.Denotingstas the memory state at instantt, it can be written as:

Where,Uare weights ofxt,Ware weights ofst-1.

Because of this structure of the RNN network,it can link current information with past information. Forth more, it can predict the current state based on current input and the last information.Due to these advantages, the RNN is used widely in the field of time series prediction,speech recognition[15],machine translation and so on.

4. INS/GNSS integration

Navigation information is collected at certain sampling rate;hence they can be regarded as a kind of time series. According to analysis in section 2,the position error δpINSof INS can be predicted utilizing the RNN, Where, the constant τ and the unknown bias static component of accelerometer and gyro can be denoted by the bias unit of RNN.

In addition, it indicates that the dynamic of the vehicle can be characterized by the change of vehicle velocity Δv and attitude Δψ in each epoch [16]. Environment is complicated, and it is not considered for the moment.Therefore,the relation of bias dynamic component with vehicle's dynamic quantities can also be learned after training by RNN. Then, the relations of INS errors with these variables can be modeled and learned by RNN with a large number of data.

Based on above conclusion, an INS/GNSS integrated system using RNN is proposed in this paper,as shown in Fig.3 and Fig.4.The suggested system architecture consists of two modes of process:train mode (Fig. 3) and prediction mode (Fig. 4).

4.1. Train mode

If the position and velocity from the GNSS are available, the system works on the train mode.The change of vehicle velocity Δv and attitude Δψ of INS with the latest position error and velocity error are used as input of the RNN.

The output is the estimated position errorand velocity errorThe differences of position and velocity between INS and GNSS are used as the supervision to train the RNN with the training criterion, which equal to:

At the same time, the estimated residuals of position andvelocity γpand γvare calculated:

Table 1 Improvement result for the proposed RNN method on simulation data.

Table 2 IMU specifications.

When

It can be judged that the learning has been done sufficiently.Where,δpand δvare the standard deviations of GNSS position and velocity, respectively.

4.2. Prediction mode

In the case where GNSS's information is not available,such as to be suppressed or interfered, the system will switch to prediction mode. Under this work condition, the system utilized the well trained RNN in section 4.1 and the change of vehicle velocity Δv and attitude Δψ of INS with the latest position error and velocity error to predict the position errorand velocity errorThen, the estimated error will be used to correct the corresponding variables as:

5. Results

In this section, the presented method is evaluated both in a statistical study with using a simulated environment and in an experiment. An aerial scenario is considered in the former, while the experiment data was collected by a test boat. The method is compared to EKF and ELM in terms of root mean square error(RMSE) of position errors and velocity errors. For all the figures shown in this section, the position errors are represented in the Transverse Mercator Projection coordinate system while the velocity error is associated with the NED frame. In this experiment,the tanh function with 10 hidden nodes is used.

Different from other literatures [10,11,16], this paper estimates tri-axial errors in an RNN network as the INS solutions are coupled.

5.1. Simulation results

The proposed method was examined in a Monte-Carlo simulation of an aerial vehicle. A ground truth trajectory was created,simulating a flight of an aerial vehicle at a 20 m/s velocity and a constant height of 1000 m above sea level.The trajectory consists of several segments of straight and level flight and maneuvers as shown in Fig. 5.

Based on the ground truth trajectory, ideal IMU measurements were generated at 100 Hz while taking into account Earth's rotation and changes in the gravity vector.For each of the 100 Monte-Carlo runs,these measurements were corrupted with a constant bias and zero-mean Gaussian noise in each axis. Bias terms were drawn from a zero-mean Gaussian distribution with a standard deviation of σ =10 mg for the accelerometers and σ =10 deg/h for the gyroscopes.The noise terms were drawn from a zero-mean Gaussian distribution with Standard deviationandfor the accelerometers and gyroscopes. Initial navigation errors were drawn from zero-mean Gaussian distributions with σ = （10，10，15） meters for position (expressed in a ECEF), σ = （0.5，0.5，0.5）m/s for velocity and σ = （1，1，1） degrees for attitude. The measured special force and angular velocity are integrated to obtain the navigation solution according to Eq. (1)～(6).In addition to IMU measurements,the aerial vehicle equipped with a GNSS receiver, operating at 1 Hz,and its measurements are corrupted with a Gaussian noise with stand deviation of 10 m in positions and 0.01 m/s in velocities. As shown in Fig. 5, one GNSS blockage epochs with the length of 15 s were simulated during the scenario presented in this section.

Fig. 9. Partial trajectory of sea trial.

Fig. 10. Reference positioning error and the RNN predicted position error in North(top), East (bottom).

Fig.11. Reference velocity error and the RNN predicted velocity error in North (top),East (bottom).

Fig.6 and Fig.7 show the results of this experiment by using the RNN method during GPS signal outage. As shown in Figs. 7 and 8,without the aid of GNSS, the system works in an INS autonomous manner, and the error gradually increases. Meanwhile, the predicted position errors are in good agreement with the original errors and the predicted velocity errors also agree fairly well with the original ones.

The detail statistical characteristics are shown in Table 1. It can be noticed that the RMSE between the RNN prediction and the system output in positions along the North, East and Down directions (in navigation coordinate) is 2.42 m, 1.86 m and 1.75 m,respectively. In additional, the RMSE between the RNN prediction and the system output in velocities along the North,East and Down directions is 0.02 m/s, 0.07 m/s and 0.03 m/s, respectively.

Table 1 shows the percentage improvement of the errors in the position and velocity obtained using RNN compared to the errors that were obtained using EKF and ELM which uses sigmoidal activation function with 7 hidden nodes.

As shown in this table, the RNN method generally achieves the best performance and ELM method followed.On the average,about 61% error reduction in the position error was achieved using RNN approach in comparison to the EKF approach, and 25% error reduction in the error against ELM. Besides, about 40% error reduction in the velocity error was achieved using RNN approach in comparison to the EKF approach, and 52% error reduction in the error against ELM. Compared with the other study [11], these results of this developed method have more error reduction. The uncertainty in the EKF approach results from linearization error of the dynamic system. Additionally, the unknown dynamics and measurement error covariance matrices result in a non-optimal EKF solution. ELM formulation provides an added advantage in case of development time savings.In addition,the ELM can absorb system dynamics or parameter uncertainty because of aging and linearization while the EKF needs a large retuning procedure [10].What's more, The RNN method utilizes the past estimated errors and vehicle's dynamic to predict the current errors in position and velocity, which makes it more accurate. As can be seen from the table,it emphasizes the ability of the RNN as a navigation solution.

5.2. Experiment results

To test the proposed method on real-world data,we make use of the sea trial data. These data were captured from the test boat sailing between Sanya, China and St. Petersburg, Russia. This test boat outfitted with a Single-axis Rotational Inertial Navigation System (RINS) and a GPS system. The system configuration is shown in Table 2.The data from these systems are collected at 1 Hz frequency. The test time is about 100 days. The whole and partial trajectories of the test boat are shown in Figs.8 and 9,respectively.

We selected a period of about 10 h of data, among which, the first 8 h of data is used as training data. The middle 2 h of data is used as validation data and the last 2 h of data is used as test data.The change of velocity and yaw from INS serves as input to RNN,and the output are errors of position and velocity of INS.However,in phase of training, the difference of positions and velocities between INS and GPS serves as target. In real navigation warfare,there may not be enough training data,so the model can be trained offline.When the available GNSS information is received,the model established offline can be intensively trained. Once GNSS is completely unavailable, switch to the predictive model when you use it.

Table 3 Improvement result for the proposed RNN method on test data.

In general, as for boat, we are more concerned with its horizontal position and velocity, hence we only studied the horizontal position and velocity errors in this experiment. Fig.10 and Fig.11 show the results of comparing origin error with predicted error.As can be seen,the original error oscillated because of the noise in the GPS measurements.However,the predicted position errors and velocities errors are in good agreement with the original errors on the whole.

Table 3 shows the percentage improvement of the errors in the position obtained using RNN compared to the position errors that were obtained using EKF and ELM. As shown in Table 3, the RNN method generally achieves the best performance and ELM method followed.On the average,about 53%error reduction in the position error was achieved using RNN approach in comparison to the EKF approach, and 39% error reduction in the error against ELM. Besides,about 74%error reduction in the velocity error was achieved using RNN approach in comparison to the EKF approach, and 18%error reduction in the error against ELM.

6. Conclusion

This paper presents a new approach for INS/GPS navigation system,which can provide a reliable positioning solution in case of GPS blockage and eliminate the complexities of EKF and the ambiguity of NN. This proposed method predicts the position and velocity errors of INS by combining the deduced error recursion formula of INS with RNN, which can be used to compensate INS error. It overcomes the disadvantage of traditional method. Both simulation data and real data verify the effectiveness in comparison with the results obtained by EKF and ELM. Furthermore, we anticipate that this proposed method can be applied in the field of muti-sensors integrated navigation system and it will be also my next research topic.

Acknowledgment

This work was supported in part by the National Natural Science Foundation of China (No.41876222) .