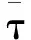向量空间上的仿射包含图

王 丽，黄 迪

(河南理工大学 数学与信息科学学院, 河南 焦作 454000)

0 引言

图论和代数是近代数学的两个重要分支，在物理、化学和计算机科学等领域有着重要的理论意义和应用价值。两者虽然研究内容不同，却有着紧密的联系:图论性质可以用来研究代数结构，代数的理论也常用来解决图论问题。因此，许多学者将它们结合起来进行研究。1988年，文献[1]首次提出交换环的零因子图概念，建立了图论与交换环理论的联系。从此，图与各种代数结构结合起来进行研究引起了学者们的广泛关注。例如，文献[2-3]研究了有限群、幂零群、内幂零群以及内交换群上幂图的相关性质。文献[4-5]分别对交换环和单演半群上的点积图进行了研究。文献[6]分类了有限群上的正则交图，并给出了交图自同构群的结构。文献[7-8]研究了图的自同态幺半群，建立起图论和半群代数理论的联系，并将半群理论用于图论的研究。文献[9-10]定义了向量空间上的非零组合图，研究了图的独立数、哈密尔顿性及边连通度等。文献[11-12]研究了向量空间上子空间包含图的欧拉性、点传递性、直径等，随后文献[13]确定了子空间包含图自同构群的结构。

目前，图和代数结构的结合研究大多与群、半群、环等代数结构相关，有关仿射几何的图研究还比较少。因此，本文定义了仿射包含图In(AV)，利用向量空间、仿射几何及图论的相关知识，讨论了图In(AV)的围长、着色数和团数等基本性质，并给出了仿射包含图同构与向量空间同构之间的关系。

1 预备知识

本文所讨论的图都是简单无向图，关于图论方面未提及的概念、符号等可参阅文献[14]。图中顶点vi的度数是与vi相关联的边的数目，记作d(vi)。没有边的图称为空图。M=v0,e0,v1,…,ek-1,vk是一条从v0到vk的长度为k的途径。如果对任意的i≠j，都有vi≠vj，则称M是一条道路。如果图G中任意两个顶点之间都存在一条道路，则称G为连通的。一条封闭的路称为圈，为了方便，常用v1,v2,…,vk,v1表示一条长度为k的圈。G的围长是G中最短圈的长度，记作g(G)。特别地，如果G不含任何圈，则g(G)=∞。如果对于G中的任意顶点v，总存在一个三角形(u,v,w)，其中u,v∈V(G)，则称G可三角化。图G的一个完全子图称为团，图G中最大完全子图所含的顶点个数是G的团数，记作ω(G)。着色数χ(G)是满足图G中相邻顶点分配不同颜色所需颜色数的最小值。

给定一个q元域上的n维向量空间V，V中k维子空间的个数[15]为:

仿射几何是由V中的向量和仿射子空间组成的，仿射子空间可由V中向量子空间经过平移得到，因此若S是一个k维子空间，则对于任意β∈V，S+β:={α+β|α∈S}是一个k维仿射子空间。规定若S=∅，且dim({β})=0，则S+β={β}。显然，若β′∈(S+β)，则S+β′=S+β。关于仿射几何未提及的内容，可以参阅文献[16]。文献[11]定义了V的子空间包含图In(V)，其点集是V中非平凡子空间的集合，任取W1,W2∈V(In(V))，若W1⊂W2或W2⊂W1，则(W1,W2)∈E(In(V))。受此启发，本文定义了仿射包含图。在下文中，除非特别提到，V都是q元域上的n维向量空间，S是V中的向量子空间。

2 仿射包含图的结构及基本性质

定义1令V是q元域F上的有限维向量空间，S是V的一个子空间且S≠V。定义仿射包含图In(AV)如下:

V(In(AV))={S+β|∀β∈V}；

E(In(AV))={(S1+α,S2+β)|S1+α⊂S2+β或S2+β⊂S1+α}。

例1令{α1,α2}是V的一组基，q=Z2，则2维向量空间上的仿射包含图In(AV)如图1所示。

图1 2维向量空间上的仿射包含图In(AV)

引理1任取S1,S2∈V(In(AV))，下列结论成立:

(Ⅰ) 若S1≠S2，则S1+α≠S2+β。

(Ⅱ)S1+α⊂S2+β的充要条件是S1⊂S2且α∈S2+β。

(Ⅲ) 若S1，S2是向量空间V的两个不同的子空间，且0≤dim(S1)=dim(S2)≤n-1， 则(S1+α,S2+β)∉E(In(AV))。

证明(Ⅰ) 若α∈S2+β，则S2+α=S2+β。由于S1≠S2，则S1+α≠S2+α，因此S1+α≠S2+β。若α∉S2+β，而α∈S1+α，因此S1+α≠S2+β。证毕。

(Ⅱ)充分性显然成立，下证必要性。若S1+α⊂S2+β，则α∈S2+β，因此S2+α=S2+β。显然S1+α⊂S2+α。对任意的β∈S1，总有β+α∈S1+α。明显地，β+α∈S2+α，因此β∈S2。由β的任意性可知S1⊂S2。证毕。

(Ⅲ)假设(S1+α,S2+β)∈E(In(AV))，则S1+α⊂S2+β或S2+β⊂S1+α。由证明(Ⅱ)可知：S1⊂S2或S2⊂S1。而dim(S1)=dim(S2)，因此S1=S2，与已知条件矛盾。证毕。

定理1In(AV)是一个n部图。

证明因为V是一个n维向量空间，所以In(AV)的顶点集可以被划分为n个互不相交的部分，即V(In(AV))=V0∪V1∪…∪Vn-1，其中，v∈Vi且dim(v)=i。由引理1的证明(Ⅲ)可得，对任意v,u∈Vi，i=0,…,n-1，总有(u,v)∉E(In(AV))。因此，In(AV)是一个n部图。证毕。

接下来，讨论仿射包含图In(AV)的顶点个数和每个顶点的度数。

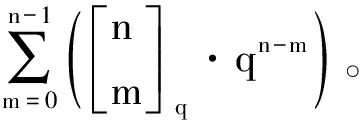
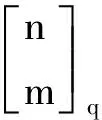
引理2任取α∈V，顶点S和S+α的度数相等。

证明假设S′⊂S，S⊂S″，其中S′和S″是向量子空间。则存在仿射子空间S′+α和S″+α，满足S′+α⊂S+α及S+α⊂S″+α。因此d(S)≤d(S+α)。

假设S′+β⊂S+α，S+α⊂S″+γ，其中S′+β和S″+γ是仿射子空间。由引理1中的(Ⅱ)可知，S′⊂S,S⊂S″。因此d(S+α)≤d(S)。综上，d(S+α)=d(S)。证毕。

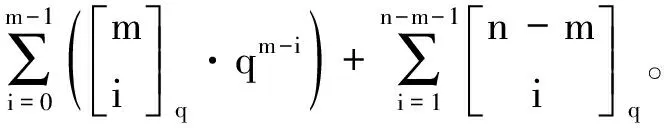
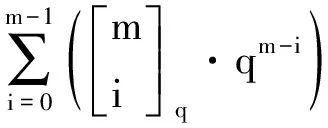
推论1若dim(V)=1，则In(AV)是一个有q个顶点的空图。

引理3若dim(V)≥2，则In(AV)是连通图。

证明任取S1+α,S2+β∈V(In(AV))，显然总存在一条连接这两点的路:S1+α,α,〈α〉,0,〈β〉,β,S2+β。 因此，In(AV)是连通的。证毕。

3 仿射包含图的相关特征

引理4若dim(V)=2，则In(AV)无奇圈。

证明任取vi∈V(In(AV))，因为dim(V)=2，所以仿射子空间vi是0维或1维的。假设存在奇圈v1,v2,…,vk,v1，其中k是奇数。由引理1中的(Ⅲ)可得:

dim(v1)=dim(v3)=…=dim(vk-2)=dim(vk)，

这与(v1,vk)∈E(In(AV))矛盾，因此引理4成立。证毕。

定理4若dim(V)=n，则In(AV)的围长为:

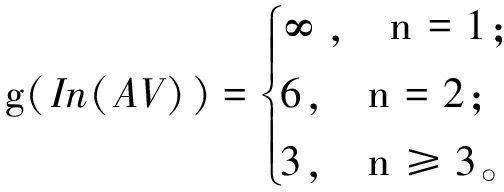
证明因为In(AV)是简单图，因此没有重边，则没有长度为2的圈。若n=1，由推论1易知g(In(AV))=∞。

若n=2，由引理4可知In(AV)没有奇圈。下证In(AV)中不含长度为4的圈。假设存在一个长度为4的圈:v1,v2,v3,v4,v1，不失一般性，令dim(v1)=dim(v3)=1且dim(v2)=dim(v4)=0。假设v1=〈α〉+γ，v3=〈β〉+γ′。若α和β线性相关，则|v1∩v3|=0。若α和β线性无关，则|v1∩v3|=1。因此至多存在一个顶点同时与v1和v3相邻，但v2和v4都与v3相邻，矛盾。因此，不存在长度为4的圈。然而，〈α〉+γ,γ,〈γ〉,0,〈α+γ〉,α+γ,〈α〉+γ是一个长度为6的圈，因此围长为6。

假定α和β是V中的两个向量，若n≥3，γ=k1α+k2β，k1,k2∈F，显然〈α〉+γ,〈α,β〉+γ,γ,〈α〉+γ是一个三角形，因此围长为3。证毕。

定理5若dim(V)≥3，则In(AV)可三角化。

证明令S是V的一个子空间，{α1,α2,…,αn}是V的一组基，γ是V中的向量。

若dim(S+γ)<2，令S=α1或〈α1〉，显然α1+γ,〈α1〉+γ,〈α1,α2〉+γ,α1+γ是一个三角形。

若dim(S+γ)≥2，令S=〈α1,α2,…,αk〉，k≥2，显然存在V中的两个子空间S′=〈α1,α2,…,αk-1〉，S″=〈α1,α2,…,αk-2〉，使得S+γ,S′+γ,S″+γ,S+γ是一个三角形。证毕。

定理6V是一个n维向量空间，当且仅当ω(In(AV))=n。

证明因为In(AV)是一个n部图，则其顶点集V(In(AV))可被表示为n个独立集的并。此外，其最大团不能包含多于每个独立集合的一个顶点，因此ω(In(AV))≤n。令{α1,α2,…,αn}为n维向量空间V的一组基，Si=〈α1,α2,…,αi〉，i=1,2,…,n-1。显然，{α,S1+α,…,Sn-1+α}是一个大小为n的团，其中α∈V。因此，ω(In(AV))=n。反过来，若ω(In(AV))=n，令dim(V)=m，由上述证明过程易知ω(In(AV))=m，因此m=n。证毕。

推论2令V是一个n维向量空间，且n≥5，则In(AV)不可平面。

证明由定理6可知，ω(In(AV))≥5，即In(AV)包含一个完全图K5作为子图，因此不可平面。证毕。

定理7若V是一个n维向量空间，则χ(In(AV))=n。

证明根据文献[17]的标记5.1.2，In(AV)是n可着色的，即χ(In(AV))≤n。任取V中的向量γ，m维非平凡子空间S，不失一般性，令S=〈α1,α2,…,αm〉。将{α1,α2,…,αm}扩充为V的一组基{α1,α2,…,αn}。显然，γ,〈α1〉+γ,〈α1,α2〉+γ,…,〈α1,α2,…,αm〉+γ,…,〈α1,α2,…,αm,…,αn-1〉+γ构成一个n个点的完全图，即对于任意的S+γ∈V(In(AV))，都有S+γ∈V(Kn)。因此χ(In(AV))=n。证毕。

定理8令V1和V2是域F上的两个有限维向量空间，则In(AV1)和In(AV2)同构的充要条件是V1和V2同构。

证明充分性: 假设V1和V2作为向量空间是同构的，令{α1,α2,…,αn}和{β1,β2,…,βn}分别为V1和V2的一组基。令τ是V1到V2的一个同构映射，并且满足:

τ(a1α1+a2α2+…+anαn)=a1τ(α1)+a2τ(α2)+…+anτ(αn)，其中a1,a2,…,an∈F。

τ(τ-1(S)+τ-1(α))=S+α，

(S+β,S′+α)∈E(In(AV1))⟺
S+β⊂S′+α或S′+α⊂S+β⟺
τ(S+β)⊂τ(S′+α)或τ(S′+α)⊂τ(S+β)⟺
(τ(S+β),τ(S′+α))∈E(In(AV2))。

因此，In(AV1)和In(AV2)同构。

必要性: 令dim(V1)=n1，dim(V2)=n2。由定理6可得:ω(In(AV1))=n1，ω(In(AV2))=n2。因为In(AV1)和In(AV2)同构，所以n1=n2，因此V1与V2同构。证毕。