钢筋混凝土受剪梁裂纹分形演化特征试验
2020-05-22赵志浩秦拥军
赵志浩,于 江,秦拥军
(新疆大学 建筑工程学院,新疆 乌鲁木齐 830047)
0 引言
自钢筋混凝土结构在建筑领域中大规模应用以来,对于混凝土损伤问题的研究已有了长足的发展。文献[1]采用声发射技术,研究了混凝土的损伤演化并建立了相应的损伤模型。文献[2]根据混凝土梁中性轴位置对梁损伤进行评估。近年来,在弯剪作用下,斜向裂纹对梁受剪破坏类型以及斜向裂纹扩展对剪切变形的影响受到广泛关注。文献[3]的研究表明:裂纹宽度对受剪裂纹传递剪力的性能有显著影响。文献[4]研究了变截面梁的受剪性能和裂纹扩展规律,得到了受压边倾角和箍筋配筋率与梁受剪性能和裂纹宽度的相关关系。文献[5]对深受弯构件的剪切开裂进行了研究,采用断裂力学理论和裂纹带抗剪理论相结合的方法,建立了深受弯构件抗剪计算模型。文献[6]采用神经网络方法对混凝土梁的抗剪承载力进行了研究,建立了抗剪承载力预测模型。文献[7]采用灰色系统理论,研究了高强钢筋混凝土梁分别在静力受剪和疲劳受剪作用下的裂纹扩展规律。
目前,国内外对混凝土梁受剪性能已经有了一定的研究成果。在受剪斜裂纹扩展规律方面,大多是对裂纹宽度发展的研究,而对裂纹的整体和局部的分布特性以及演化规律的研究相对较少。由于裂纹扩展路径具有复杂曲折的特点,传统的方法对裂纹扩展的研究较为局限,对裂纹整体和局部的分布状况难以定量,而分形理论作为研究不规则、非线性图形的有力工具,能够将裂纹曲折且无序的几何特征进行量化。分形理论创始人Mandelbrot研究发现混凝土开裂面的不规则形貌具有分形特性[8],其后大量研究人员应用分形理论对混凝土受弯断裂过程进行了研究[9-12]。文献[13]的研究表明:混凝土梁受静载作用下的裂纹具有分形特征,因此分形几何可以定量描述裂纹的扩展状态。近年来,应用分形理论分析混凝土构件在外部荷载作用下表面裂纹拓展规律方面,多为针对钢筋混凝土受弯梁的研究[14-16],而国内对受剪构件的相关研究还比较少。
为探究剪跨比和箍筋配筋率对裂纹演化的影响,本文通过进行不同剪跨比和箍筋配筋率的混凝土梁受剪破坏试验,采用分形理论对裂纹发展状况进行了定量分析,研究了钢筋混凝土梁受剪破坏过程中力学性能变化与裂纹演化规律的关系。
1 试验概况
1.1 试件设计与制作
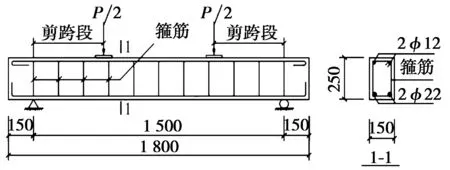
图1 试验梁尺寸及配筋图(单位:mm)
文献[17]研究表明:剪跨比和箍筋配筋率对受剪混凝土梁的表面裂纹扩展有显著影响。本文设计了以剪跨比和箍筋配筋率为变量的5片试验梁,采用C30强度等级的混凝土,立方体抗压强度fcu=33.1 MPa,轴心抗压强度fc=27.9 MPa,受力纵筋采用HRB335级钢筋,箍筋采用HPB300级钢筋。梁的尺寸为长×宽×高=150 mm×250 mm×1 800 mm,保护层厚度为20 mm,试验梁尺寸及配筋图如图1所示。试验剪跨比分别为1.5、2.0、2.5,箍筋配筋率分别为0.25%、0.36%、0.45%,5片矩形截面简支梁参数见表1。为确保混凝土梁不发生受弯破坏,本试验设计了足够的底部受力纵筋以抵抗跨中弯矩作用。
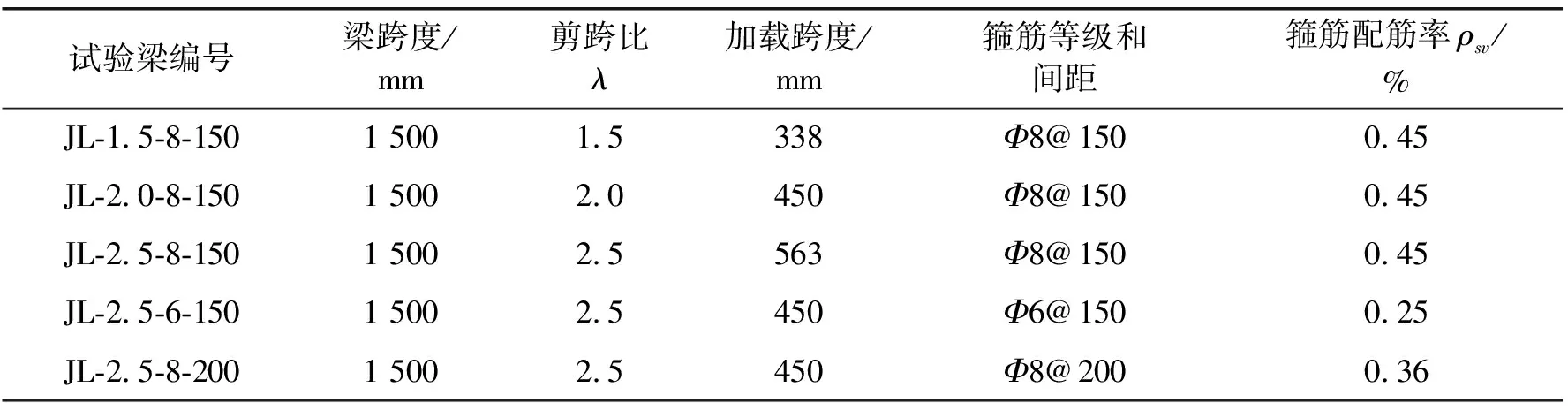
表1 5片矩形截面简支梁参数
1.2 加载方案

图2 加载装置和位移测点布置
试验采用量程为600 kN的JSF300T伺服压力机对试验梁进行加载,采用两点对称加载。加载装置和位移测点布置如图2所示。荷载通过分配梁对称加载在试验梁上,通过控制加载点与支座的距离来调整剪跨比。
试验梁加载模式为单调静力分级加载,按GB/T 50152—2012《混凝土结构试验方法标准》[18]中的标准对试验梁进行加载。试验的加载过程分为开裂前和开裂后两个阶段,开裂前施加的每级荷载为理论破坏荷载的10%,当达到理论开裂荷载的80%后,每级荷载降为破坏荷载的5%,以确定试验梁开裂时荷载的准确值。开裂后每级荷载为破坏荷载的10%,每级荷载持荷10 min,直至构件破坏。在向构件施加每级荷载后记录相应的荷载数值、试验梁挠度以及裂纹的发展图形。
2 裂纹分形特征
2.1 裂纹分形维数计算方法
分形维数是评价几何图形分形特征的重要参数,表示几何图形局部与整体的相似程度。混凝土梁受剪裂纹的发展表现出复杂无序的特点,但其是否具有统计意义上的分形特征,及其在何种标度范围内符合分形特征尚需验证与研究。为定量评估构件表面裂纹的分形特征,本文采用计盒法计算裂纹的分形维数。计盒法的操作过程为:以边长为r的方盒覆盖裂纹区域,统计内部含有裂纹的方盒数量记为N(r),缩短方盒边长并重复以上过程,最终获得一系列的(r,N(r))数据。拟合lnr-lnN(r)曲线,如果得到的曲线为线性相关的直线,则证明裂纹具有分形特征,裂纹的分形维数Df=-lnN(r)/lnr。为研究构件裂纹分形特征对梁受剪性能的影响,计盒法需要确定方盒的尺寸范围,尺寸的上限为裂纹间距,下限为骨料最大粒径[19]。此次试验混凝土中骨料的粒径为5~30 mm,裂纹平均间距约为150 mm。因此,本文方盒尺寸分别为30 mm、40 mm、50 mm、60 mm、70 mm、80 mm、90 mm、100 mm、110 mm、120 mm、130 mm、140 mm和150 mm。
2.2 试验梁裂纹分形特征
以试验梁JL-2.5-8-200为例,在各级荷载下梁侧面裂纹分布如图3所示。当试验梁达到开裂荷载36 kN时,纯弯段和剪弯段出现一些微小裂纹,如图3a所示;当荷载达到72 kN时,纯弯段裂纹向上延伸,在剪弯段临近纯弯段的区域由于剪力和弯矩的共同作用,产生了弯剪斜裂缝,如图3b所示;当荷载达到116 kN时,剪弯段产生腹剪斜裂缝并贯通试验梁,如图3c所示;当荷载达到150 kN,试验梁剪弯段出现新的裂缝并不断发展,而纯弯段裂缝几乎停止了扩展,如图3d所示;当临近破坏时,剪弯段斜裂纹充分发展,纯弯段裂缝只有少量延伸,如图3e所示。由图3可以看出:在外部荷载作用下,梁表面裂纹随荷载增加不断扩展和延伸,裂纹形状逐渐变得曲折,并且其分布变得越来越复杂。各级荷载作用下裂纹的lnN(r)-lnr曲线如图4所示。从图4中可以看出:拟合得出的lnN(r)-lnr曲线具有良好的线性相关性,而且拟合直线的斜率随荷载增大而增大,表明裂纹分形维数随荷载增大而增大,与图3所显示的裂纹扩展演化趋于曲折和复杂的规律一致。经分析计算,各试验梁lnN(r)-lnr曲线均符合线性相关关系,拟合直线的斜率(即裂缝分形维数Df)和拟合优度R2见表2。由表2可知:R2为0.968 9~0.974 7,可见lnN(r)-lnr曲线的拟合程度很高;拟合得到的分形维数为0.976 9~1.276 7,说明混凝土受剪产生的斜裂纹具有良好的分形特征。各试验梁的裂纹分形维数均表现出随荷载增大而增大的趋势,与裂纹曲折而复杂的演化趋势相一致,因此可以用分形维数对裂纹的演化进行定量描述。

(a) 荷载P=36 kN

(b) 荷载P=72 kN

(c) 荷载P=116 kN

(d) 荷载P=150 kN

(e) 荷载P=189 kN
图3 各级荷载下JL-2.5-8-200试验梁侧面裂纹分布

图4 各级荷载下JL-2.5-8-200试验梁ln N(r)-ln r曲线

表2 各级荷载下梁表面裂缝分形维数Df及拟合优度R2
3 裂纹分形特征与构件力学性能的关系
3.1 裂纹分形维数与荷载的关系
试验梁裂纹分形维数-荷载关系曲线见图5。如图5所示,随着荷载增大,梁表面裂纹的分形维数呈上升趋势。随外部荷载增大,试验梁的裂纹逐渐开展,裂纹的数量逐渐增多且已有的裂纹不断延伸,形状变得曲折而复杂,因此梁表面裂纹的分形维数随之增长,受剪梁的损伤随荷载增加越来越严重。从图5a中可以看出:在同等级的外部荷载作用下,剪跨比越大,裂纹的分形维数越大。这可能是由于当剪跨比较小时,梁剪弯段的拉应力相对较小,混凝土在拉应力作用下裂纹扩展相对较为缓慢,因而分形维数较低;随着剪跨比的增大,剪弯段拉应力提高,混凝土裂纹开展越发充分,分形维数也就越大。从图5b中可以看出:在同等级荷载下,梁的箍筋配筋率越高,裂纹分形维数越小。这是由于随着箍筋配筋率的提高,在相同荷载等级下箍筋承载的应力越大,混凝土所承受的应力越小,因此,混凝土受剪裂纹开展相对较为缓慢,在相同等级荷载作用下随箍筋配筋率的增大,裂纹分形维数越小。
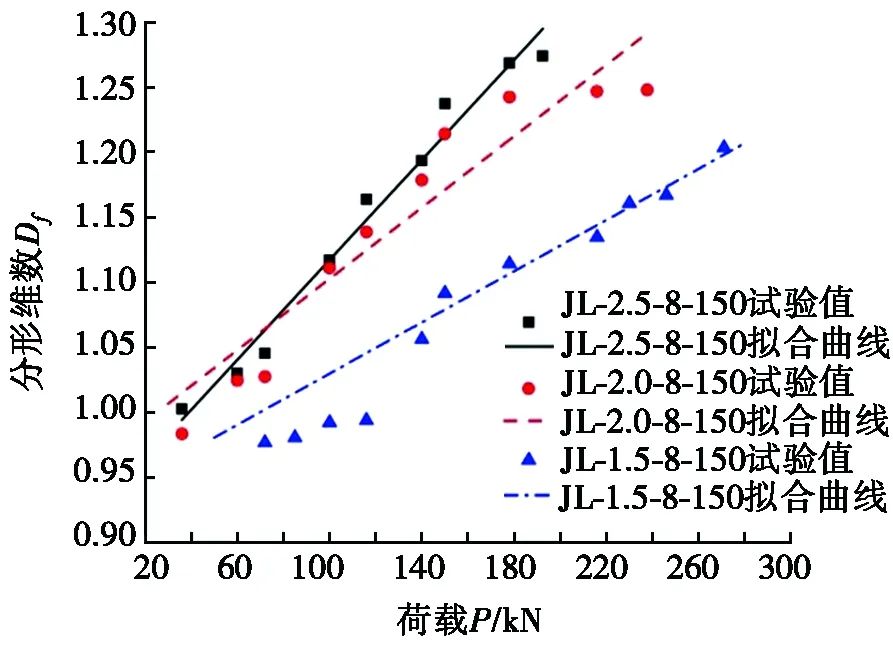
(a) 不同剪跨比下Df-P曲线
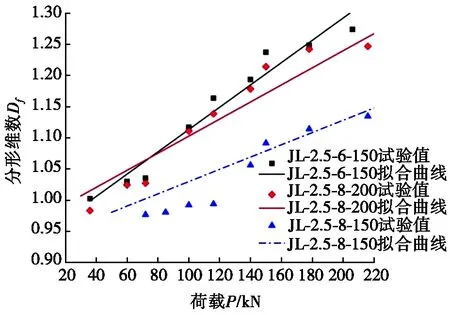
(b) 不同箍筋配筋率下Df->P曲线
图5 试验梁裂纹分形维数-荷载关系曲线
从图5中可以看出:试验梁裂纹分形维数Df与荷载P成线性正相关关系,拟合直线得到:
Df=aP+b,
(1)
其中:a为拟合直线的斜率;b为拟合直线的截距。在本研究中,a、b为与构件箍筋配筋率和剪跨比有关的系数,为待定系数。试验梁Df-P拟合曲线的拟合系数见表3。由表3可知:在配筋率相同的情况下,即ρsv=0.45%时,随剪跨比从1.5增至2.0和2.5,斜率a分别增大了39.8%和82.7%;在剪跨比相同的情况下,即λ=2.5时,随箍筋配筋率从0.25%提高到0.36%和0.45%,a的值分别减小了3.6%和7.7%。这是由于随着剪弯段长度的增大,混凝土梁剪弯段所承受的弯剪作用增强,剪弯段受剪裂纹增多且发展更快,因此裂纹分形维数随荷载增大的速率随剪跨比增大而增大;随着箍筋配筋率的增大,箍筋对裂纹的约束作用增强,裂纹的增长过程放缓,裂纹分形维数增长速率降低。
系数b为当试验梁所承受荷载为0 kN时裂纹的分形维数,因此,可认为系数b反映了试验梁中初始损伤状态。系数b的值为0.931 47~0.965 69,各试验梁系数b的差值在3%以内,表明各试验梁中损伤状况差别微弱。由于试验梁采用相同配合比的混凝土,在试件制作的过程中环境和制作工艺存在一定的差异,所以混凝土中微裂纹等损伤也存在微弱的差异,这与系数b所反映的混凝土中损伤差异状况一致。

表3 试验梁Df-P拟合曲线的拟合系数
通过式(1)可以看出:混凝土梁受剪破坏过程中,裂纹分形维数与梁所承受的荷载之间存在良好的定量关系,可以由剪跨比、箍筋配筋率以及裂纹分形维数等信息推算出混凝土梁所承受的外部荷载,进而对受剪梁的受力状态进行评估。
3.2 裂纹分形维数与跨中挠度的关系
钢筋混凝土梁在外部荷载作用下发生挠曲变形,文献[20]的研究表明:混凝土梁的剪切变形约占总变形的30%,斜向开裂后的混凝土梁截面刚度降低而挠度增大。考虑到剪弯段变形对混凝土梁挠曲变形的贡献和裂纹开展对混凝土梁弯曲变形的影响,本文研究了梁剪弯段裂纹分形特征对梁挠度的影响。混凝土梁跨中挠度与梁表面裂纹分形维数相关关系曲线如图6所示。从图6中可以看出:混凝土梁开裂后跨中挠度随裂纹分形维数的发展先经历了弹塑性阶段,在此阶段跨中挠度随裂纹分形维数增大而增大,但增速缓慢;之后混凝土梁进入塑性阶段直至破坏,跨中挠度增长迅速,这可能是由于在弹塑性阶段裂纹的演化多以裂纹增加和裂纹延伸为主,而进入塑性阶段后钢筋屈服,裂纹演化以宽度增长为主。以幂函数拟合跨中挠度和裂纹分形维数的关系,两者的关系式为:
(2)
其中:f为跨中挠度,mm;A和B为与剪跨比和箍筋配筋率有关的待定系数。从图6a可以看出:随着试验梁的剪跨比增大,拟合曲线的曲率减小。从图6b中可以看出:随着试验梁箍筋配筋率增大,拟合曲线的曲率减小。各试验梁Df-f曲线的拟合系数见表4。系数A反映了拟合曲线的曲率,即混凝土梁跨中挠度随裂纹分形维数增长的速率。从表4中可以看出:配筋率为0.45%的试验梁,随剪跨比从1.5增至2.0和2.5,系数A的值分别减小了0.95%和3.87%,表明跨中挠度随裂纹分形维数增长的速率随剪跨比增大而降低。其原因是随剪跨比增大,剪弯段的箍筋数量增多,从而抑制了剪切裂纹的发展,且由于箍筋数量增多,其耗能增多,用于变形的能量减少,因此增长速率降低。剪跨比为2.5的试验梁,随箍筋配筋率从0.25%增大至0.36%和0.45%,系数A的值分别减小了7.37%和7.56%,表明随箍筋配筋率提高,梁的跨中挠度随裂纹分形维数增长的速率降低。其原因是随箍筋配筋率提高,剪弯段内箍筋含量提高,抑制裂纹扩展的能力增强且消耗的能量增加,用于变形的能量减少,因而跨中挠度随裂纹分形维数增速降低。
系数B反映了试验梁开裂前变形情况,B值越大表明试验梁开裂前变形越大。由表4可知:对于配筋率为0.45%的3个试验梁,剪跨比为1.5的试验梁的B值远大于剪跨比为2.0和2.5的试验梁,其B值分别比剪跨比为2.0和2.5的试验梁增大66%和59%。对于剪跨比为2.5的3个试验梁,配筋率为0.45%的试验梁的B值远大于配筋率为0.36%和0.25%的试验梁,其B值分别比配筋率为0.36%和0.25%的试验梁增大90%和77%。这是由于相同配筋率下,剪跨比为1.5的试验梁开裂荷载远大于剪跨比为2.0和2.5的试验梁,而剪跨比为2.0和2.5的试验梁开裂荷载相近;在相同剪跨比下,配筋率为0.45%的试验梁开裂荷载远大于配筋率为0.36%和0.25%的试验梁,而剪跨比为0.36%和0.25%的试验梁开裂荷载相近,在较大的荷载作用下试验梁所发生的变形更大。

(a) 不同剪跨比下Df-f曲线
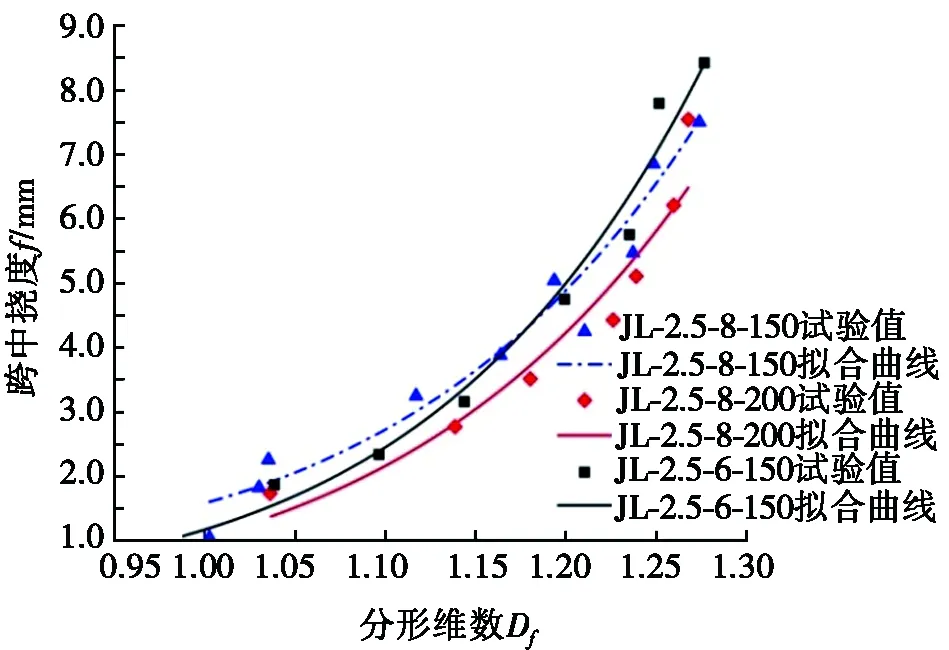
(b) 不同箍筋配筋率下Df-f曲线
图6 试验梁裂纹跨中挠度-分形维数关系曲线

表4 试验梁Df-f拟合曲线的拟合系数
4 结论
(1)混凝土梁剪弯段裂纹发展具有统计意义上的自相似特性,受剪裂纹具有明显的分形特征,混凝土梁受剪裂纹的分布特征可以采用分形维数来描述。
(2)混凝土受剪梁在剪力作用下表面裂纹的演化是一个增维的过程,随剪力增大,受剪裂纹的分形维数线性增大,分形维数为0.976 9~1.276 7。箍筋配筋率越高,梁表面裂纹分形维数增长越慢;剪跨比越高,梁表面裂纹分形维数增长越快。
(3)建立了混凝土梁挠度与梁表面裂纹分形维数之间的相关关系,梁表面裂纹分形维数与荷载成线性相关关系,与跨中挠度成幂函数关系。随裂纹分形维数的增大,受剪梁跨中挠度也在增大,且增速随箍筋配筋率和剪跨比增大而降低。
