DE算法改进的炼焦能耗RBF预测模型

陶文华，陈 娇，桂运金，孔平平

（辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001）

焦炭是冶炼、化工以及机械制造等行业生产中主要原料和燃料，是工业生产中不可或缺的物质[1]。受目前技术与设备的限制，影响炼焦能耗的因素众多。比如炉门的开启，炉门与炉墙之间的缝隙，目标火道温度，配合煤挥发分、水分等。目标火道温度可以在线实时监测，而配合煤挥发分、水分则无法实时在线监测，为了解决炼焦能耗无法实时测量的问题，科研工作者通过对生产过程中数据的积累与经验归纳，构建相应的预测模型，对比误差大小，选择合适的模型用于实际生产。

对于炼焦能耗的预测，国内外专家学者一直在进行研究。文献[2]通过对炼焦生产机理的分析，建立改进的BP神经网络的炼焦能耗模型。舒广[3]设计了“焦化回收能量流有序化工艺”，从根本上解决了广泛存在的焦化回收系统高能耗、高污染的难题。文献[4]针对焦炉炉门对炼焦能耗的影响，对焦炉炉门服务车进行改进来满足生产需要，减少炼焦能耗，提高企业效益。文献[5]针对炼焦过程中炉门全开时冷风吸入热量外溢增加能耗的问题，增加炉门位置检测传感器，实现炉门出钢过程中处于半开控制状态，以此来降低能耗。文献[6]提出通过设备升级和技术改造的方法来减少炼焦工序能耗。文献[7]通过对粗钢能耗的影响因素进行分析，利用实际生产数据，基于基因表达规划(GEP)建立粗钢能耗的预测模型，利用预测模型的可预测性，降低企业的生产成本，对企业的生产过程进行指导。文献[8]针对煤炭能源的消耗建立了基于斯特帕特模型的向量自回归（VAR）模型，通过GM（1，1）模型的预测结果。文献[9]为了优化能源配置，实现节能减排的目的，建立了一套具有数据采集、统计分析和预测等功能的能效评价指标体系，对钢铁实际生产过程中能源消耗的动态检测进行模拟实验。

本文以炼焦生产过程为例，从炼焦能耗模型入手，提出利用差分进化（Differential Evolutionary，DE）优化的RBF神经网络对炼焦能耗进行预测的模型，通过实际生产过程中的实例进行验证分析。分析结果表明，该模型不仅收敛速度快、学习效率高，而且具有较好的适应性和预测精度。

1 炼焦能耗影响因素分析

影响炼焦能耗的主要因素包括炼焦热、炉体散失热以及废气携带热[10]。根据炼焦耗热量定义可知，影响炼焦能耗的主要因素是炼焦热，它是焦炉热平衡中产生的有效热，是实际生产中衡量炼焦生产操作工艺水平的一项重要指标[2]，主要取决于目标火道温度、配合煤水分、配合煤挥发分、烟道吸力及结焦时间等因素。

1.1 目标火道温度

目标火道温度是指在焦炉各个燃烧室测点所测得的火道温度平均值，分别为机侧火道温度(T1)和焦侧火道温度(T2)[11]。目标火道温度是保证焦饼成熟度的一个重要指标，同样是衡量炼焦能耗的重要因素之一。在规定的结焦周期内，目标火道温度过高，单位成品的能耗迅速增加，“扒焦”现象便会出现；如果目标火道温度太低受热不均，则不利于炼焦过程的正常运行。

1.2 配合煤水份

配合煤水份(Md)对于炼焦能耗的影响不容忽视。在炼焦生产过程中，当胶质层中产生的热解气体使煤中的水份摩尔分数低于8%时，则不会产生额外的炼焦热损失；当煤中的水份高于8%时，水份对炼焦热则会产生较大的影响，水份每增加1%，相应的炼焦热就会增加30 kJ/kg，炼焦能耗从而增加。

1.3 配合煤挥发分

配合煤挥发分(Vdaf)的含量直接影响焦炭机械及反应特性，对炼焦能耗的大小产生间接影响。当配合煤挥发分过高时，会增加反应过程中的吸热量，影响焦炉的正常生产过程；当配合煤挥发分过低时，则推焦困难，生产时间增加，炼焦能耗增大。

1.4 烟道吸力

烟道吸力(xl)的大小对炼焦能耗有着重要的影响。在焦炉加热过程中，控制烟道吸力能够实现最佳燃烧状态。当烟道吸力过小时，煤气燃烧不充分，使炼焦耗热量增加；烟道吸力过大时，使燃烧产生的废气量增大，带走的热量增加，从而使炼焦能耗增加。

1.5 结焦时间

炼焦能耗的大小还与结焦时间(t)的长短有密切的关系。若焦炉内的结焦时间过短，则需要消耗更多的煤气来提高火道温度；结焦时间过长，则会增加炼焦热，能耗损失增大。

2 DE优化RBF神经网络

炼焦过程是一个多变量、时变、复杂不定的工业炼化过程。炼焦能耗很难实现在线测量，为了最大限度地减少焦炉能耗节约资源，本文建立了基于差分进化算法优化的RBF神经网络炼焦能耗预测模型。

2.1 RBF神经网络预测模型

RBF神经网络是一种三层式前向型结构的网络，由输入层、隐含层和输出层三部分构成[12-13]。根据对炼焦机理的分析，确定RBF神经网络的输入输出，隐含层径向基函数选择高斯函数。高斯函数表达式为：

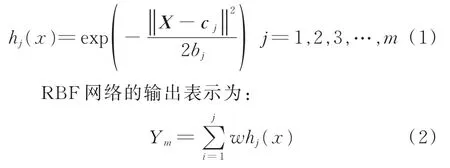
式中，X为输入向量；cj为第j个径向基函数的中心向量；bj为隐含层基函数的宽度；hj为隐含层第j个神经元的输出；Ym为输出变量；w为RBF神经网络隐含层到输出层的权值。

2.2 差分进化算法

差分进化算法[14]，是利用全元素搜索、实数编码、差分元素简单变异以及一对一择优选取的筛选策略[15-17]。其逻辑算法原理简单易懂，该算法具有较强的全局搜索能力及较高的求解精度[18]。实现方式与遗传算法非常相似，同样基于变异（mutation）、交叉（crossover）和选择（selection）三个基本操作。首先该算法选用当前全体元素的个别元素进行变异，然后采用交叉操作方式获取中间元素，最后采用选择操作将父代元素与中间元素进行择优比较并进行保留，组成新的下代元素[19]。

2.2.1 变异操作 以全体元素的父代元素为基础，利用不同的三个个体，其中一个个体为基向量，另外两个个体互相作差形成差分量。差向量的个数及基向量的选取有以下几种方式[20-21]：

（1）以随机选择的个体为父代基向量，采用一个差向量生成变异个体。

（2）以当前种群最优个体为父代基向量，采用一个差向量生成变异个体。

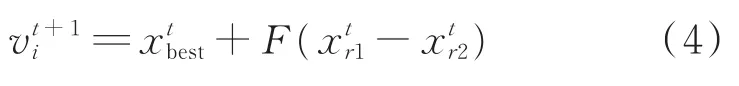
（3）以随机选择的个体为父代基向量，采用两个差向量生成变异个体。

（4）以当前种群最优个体为父代基向量，采用一个差向量生成变异个体。

式中，r1、r2、r3、r4、r5为随机产生的分布在[1，Np]的互异不相等的自然数，其中Np为种群个数；为随机产生的变异个体；xbest为最优个体；F为变异因子，影响偏差变量的放大作用。

2.2.2 交叉操作 交叉操作就是互换变异个体向量与目标向量的信息进而形成新个体向量，称之为实验向量[22]。交叉方式有以下两种。

二项式交叉：

式中，cr∈[0，1]为交叉因子。

指数交叉：

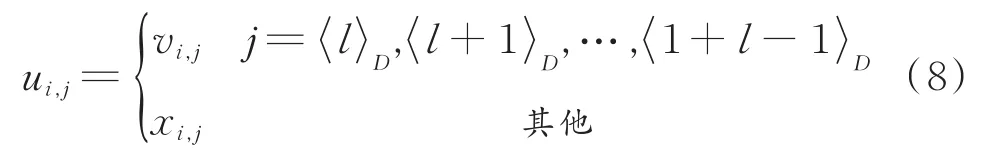
式中，l为[1，D]中的任意一个随机整数。

2.2.3 选择操作 差分进化算法采用贪婪的搜索策略选择能够进入第g+1代种群中的个体[23-24]。在实验向量个体与目标向量个体竞争过程中，如果前者的适应度优于后者，则在第g+1式中将vi(g)取代xi(g)作为子代，否则保留xi(g)，表示为：

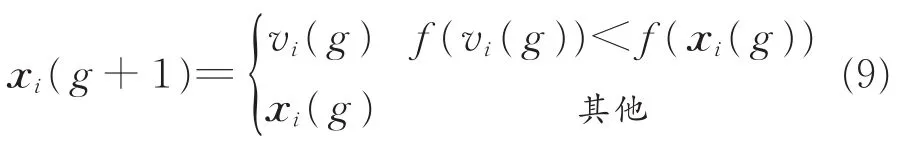
式中，xi(g+1)为下一代的目标向量。

差分进化算法流程如图1所示。

图1 差分进化算法流程

2.3 DE-RBF神经网络预测模型

建立预测模型过程中，合理有效地选择RBF神经网络的参数很关键。本文径向基函数选用高斯函数，利用梯度下降法确定网络的隐含单元基函数的中心（ci）、宽度（bi）以及隐含层与输出层之间的连接权值（wki）。由于RBF神经网络存在收敛速度慢，精度低的问题，取得的参数不是最优，因此采用差分进化算法优化RBF神经网络的参数，得到最优参数，提高网络的预测精度。基于DE-RBF网络预测模型流程如图2所示。

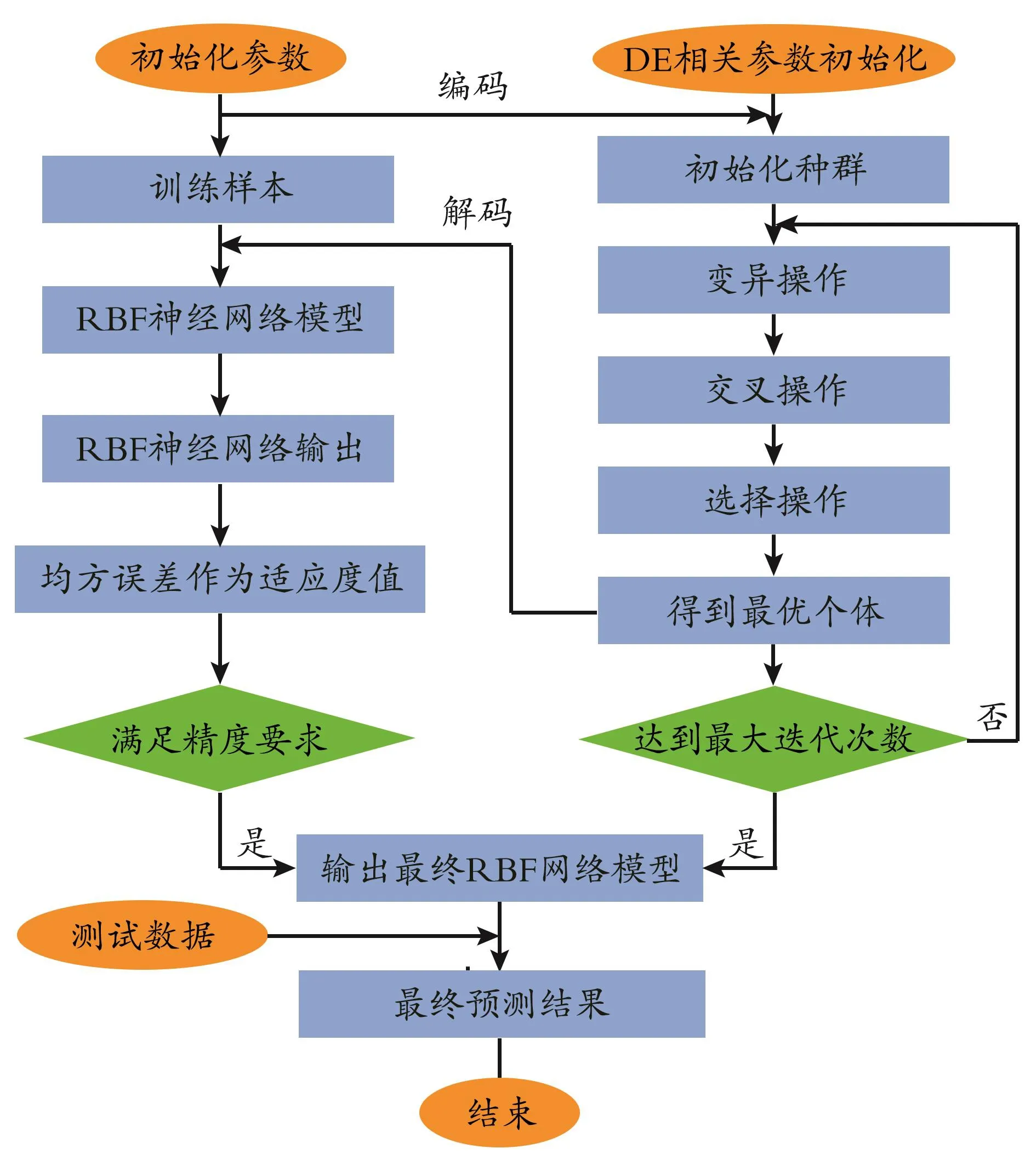
图2 基于DE-RBF网络预测模型流程图

基于DE-RBF网络预测模型流程优化步骤为：

(1)初始化参数设置。根据实际目标问题，保证变异变量足够设定种群数量（Np）。变异因子（F）是一种控制参数[25]，决定偏差变量比例、影响算法收敛速度，为了使算法逃出局部极小值，收敛速度快且能收敛到全局最优点，F取值范围为[0.4，1.0]。交叉因子（cr）是[0，1]内的实数，控制一个实验向量参数来自变异向量的概率，cr偏大算法会出现早熟现象。最大迭代次数（Gmax）取值越大，其最优解越精确，但增加算法计算时间，因此迭代次数选择范围为[100，200]，目标误差值选定为 0.001。

(2)RBF网络计算。用已有样本输入输出数据对RBF网络进行训练，计算出模型输出以及样本输出与模型输出之间的误差。

(3)确定适应度函数。适应度函数用来描述种群中个体优劣程度。本文将均方误差作为适应度函数，使RBF网络的误差精度通过驯良达到。适应度函数表达式为：

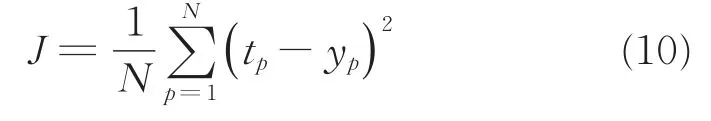
式中，N为训练样本总数；tp为期望输出值；yp为实际的输出值。

(4)判断适应度值是否满足目标误差的要求，若满足要求则结束运行，若不满足则转入下一步。

(5)若迭代次数达到最大次数，则结束算法，否则转入下一步。

(6)进行差分进化算法的变异、交叉和选择操作。其中，变异操作过程采用随机选择的个体为父代基向量，采用一个差向量生成变异个体，其表达式为：

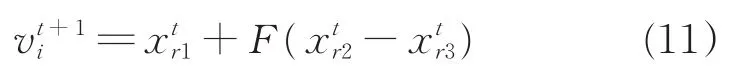
对于交叉操作，仍采用二项式交叉方法，其表达式为：

式中，rj为第j个[0，1]的随机数。

选择操作根据公式（10）得到满足目标误差要求的最优个体，即最优的RBF网络结构参数。

(7)利用当前已得到的最优RBF网络模型对预先准备的测试数据进行实际预测，得到最终的预测数据并加以分析论证。

3 炼焦能耗模型预测

采用100组来自于钢厂实际生产中的数据进行网络训练，另取30组数据对训练后的网络进行预测验证。

3.1 数据预处理

选取的数据来源于实际生产过程，数据在记录、筛选、保留过程中，可能会由于其他因素使数据产生变化，而且这些数据维数高且量纲不同，绝对值相差较大，会对模型的预测精度产生很大的影响。因此需要对输入参数集中进行归一化处理，将输入参数变换到[0，1]范围。其变换公式为：

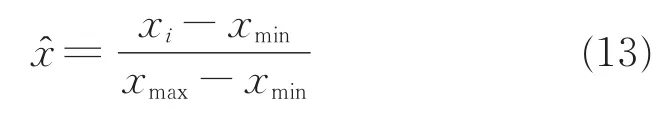
式中，xmin、xmax为每组数据变量中的最小值和最大值；xi为归一化前的变量值；为归一化后的的变量值。

3.2 炼焦能耗预测模型建立

经过对炼焦能耗影响因素的分析，建立一个RBF神经网络预测模型如图3所示。

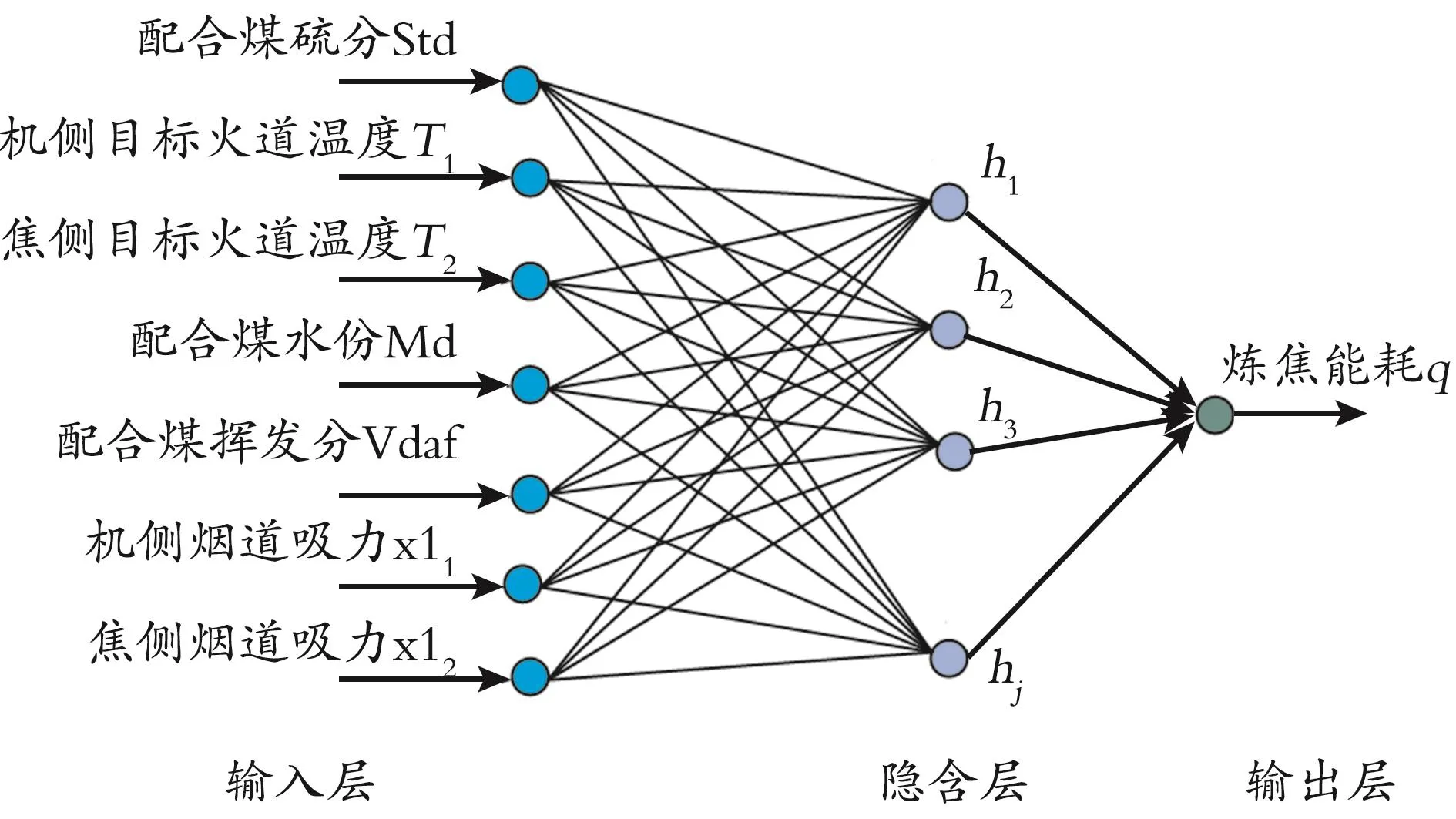
图3 RBF神经网络预测模型

基于建立的预测模型，利用归一化处理后的数据对预测网络进行训练，然后利用另外选取的30组归一化处理数据进行预测检测，将最终结果与实际数据进行比较，RBF炼焦能耗预测结果如图4所示。

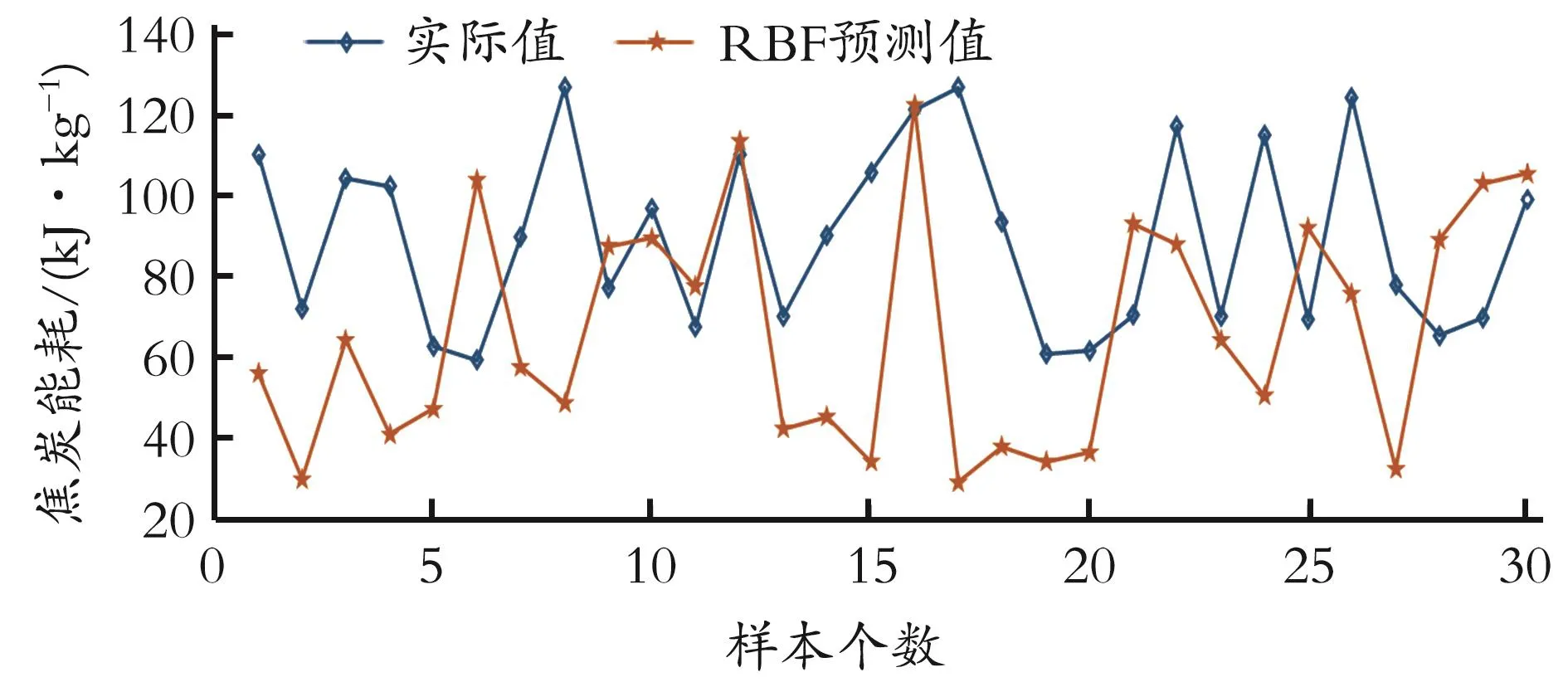
图4 RBF炼焦能耗预测结果

在训练过程中取误差精度为0.001，由RBF神经网络经过58次迭代使得误差精度小于0.001。因RBF神经网络在预测过程中具有局限性、精度差、迭代速度较慢的问题，利用差分进化算法较强的全局搜索能力对RBF神经网络的参数进行优化，利用优化后的实验参数对网络进行训练，得到的预测网络精度与迭代速度明显提高。在DE优化RBF参数后的神经网络预测模型中，RBF网络初始参数保持不变，对参数进行编码得到初始化种群，种群规模为 30，F=0.8，cr=0.5，最大迭代次数取 100，误差精度为0.001。利用DE算法得到最优的RBF神经网络参数，将参数解码带回到RBF网络中，同样采用归一化处理后的参数再次进行训练、预测，DE-RBF炼焦能耗预测结果如图5所示。

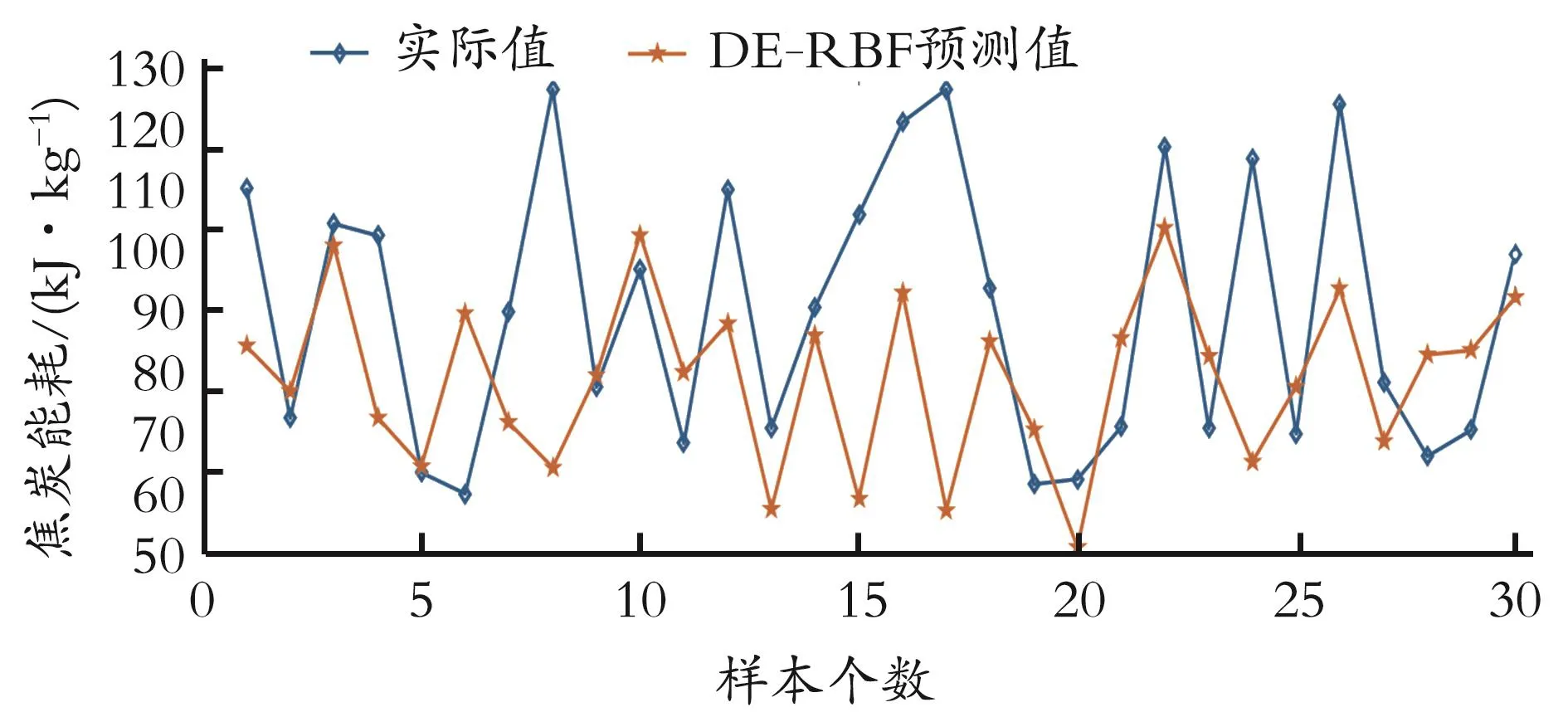
图5 DE-RBF炼焦能耗预测结果

采用最大绝对误差Emax、均方根误差RMSE、平均绝对百分比误差MAPE作为算法与测准确度的指标，其数学表达式为：

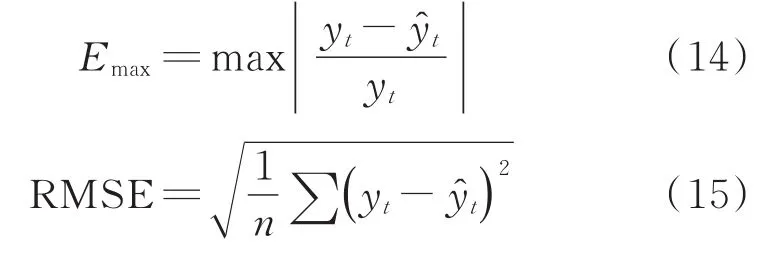
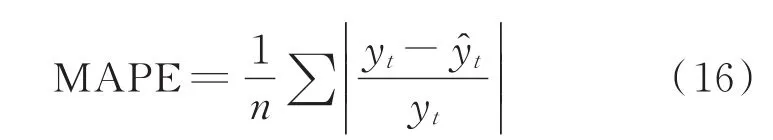
式中，n为测试样本总数；yt为能耗的真实值；为能耗的预测值。

Emax反映了预测值相对于真实值的最大偏离程度；RMSE反映了预测值与真实值之间的离散程度；MAPE反映了预测值的平均偏离程度。最大绝对误差Emax、均方根误差RMSE、平均绝对百分比误差MAPE这三个指标值越小，说明模型预测效果越好。两种模型的指标比较结果如表1所示。从表1可以看出，DE-RBF神经网络模型中的三个指标值均小于RBF神经网络模型。其中，最大相对误差为0.517，较RBF神经网络降低了0.185；DE-RBF均方根误差为67.23，明显小于RBF神经网络的117.45，说明改进后的网络预测结果相对稳定；平均绝对百分比误差值为0.130 6，较RBF神经网络模型提高了9.5%，说明炼焦能耗的预测精度得到了提高。另外，从迭代次数来看，当均方误差达到目标误差值时所需的迭代次数减少，说明优化后加快了运行速度。

表1 两种模型的指标比较结果

4 结 论

针对炼焦生产过程工艺流程复杂、影响因素众多、炼焦能耗预测模型建立困难等问题，提出差分进化算法优化RBF神经网络的炼焦能耗预测模型。DE算法具有全局搜索能力强大、收敛速度快、稳定性能高效等优点。经过分析论证可知，相对于RBF神经网络炼焦能耗预测模型，DE-RBF神经网络炼焦能耗预测模型的学习能力和预测能力都更好。仿真结果表明，将差分进化算法与RBF神经网络相结合进行炼焦能耗预测模型具有很好的应用前景。