基于Minimax理论的多机电力系统干扰抑制控制器设计

常 玲， 井元伟

(1.东北大学 信息科学与工程学院， 辽宁 沈阳 110819； 2.沈阳城市建设学院 信息与控制工程系， 辽宁 沈阳 110167)

电力系统运行过程中，存在许多影响其稳定性的因素，如线路上负荷的波动、电力元件的短路故障以及失去子系统间联接等情况.为了保障用电的可靠性，电力系统应具有承受干扰的能力.同时，在最坏的情况下，系统仍可控且无大范围连锁式停电的情况发生.文献[1]采用微分几何与线性最优控制理论相结合方法，完成了单机电力系统的励磁与汽门控制设计.文献[2]提出一种新的改进的直接反馈线性化方法，并应用于电力系统的自适应非线性励磁控制，有效调节了电力系统的机端电压.文献[3]采用自适应backstepping的方法，讨论了单机电力系统鲁棒控制器设计问题，所得结果可使系统对干扰具有快速的收敛性能.虽然单机电力系统的鲁棒控制方法逐渐成熟，但是随着并入电力系统的发电机组越来越多，导致大规模、超高压机组互联等电力系统的非线性、强耦合性能越来越突出.因此，多机电力系统的稳定性和抗干扰能力的研究尤为重要.随着学者们对Hamilton理论的深入研究，使得其在电力系统中得到了较好的应用与实现.文献[4]给出了一般系统广义耗散Hamilton实现的充分条件，该条件进一步应用到了简单的电力系统中，得到了双机系统的局部耗散Hamilton实现.文献[5]基于非线性微分-代数系统(NDAS)的Hamilton实现问题，提出了一种改进的Hamilton系统，通过重构系统结构矩阵对H函数进行能量整形，给出了镇定控制器的设计方法.文献[6-7]结合广义Hamilton能量理论，研究了电力系统控制器的设计问题.文献[8]分别在两种情况下建立了结构保持多机电力系统的广义Hamilton模型.其中，一种情况为不考虑转移电导，另一种情况为同时考虑自导纳和互电纳，而不考虑互电导.文献[9]则在考虑互电导的情况下，构建了改进的Hamilton系统，可称为伪广义Hamilton系统.对于多机电力系统的干扰抑制问题，学者们在L2干扰抑制和自适应H∞控制上已经取得了许多成果.但是在处理干扰问题上，多采用对不等式进行放缩的方式，这从某种程度上增加了系统的保守性.

经研究发现，基于Minimax理论的控制方法对于抑制突发性的大干扰具有较好效果[10]，且已有结果[11]将其应用于单机电力系统的干扰抑制问题研究中.文献[10]针对具有晶闸管控制串联补偿器(thyristor controlled series compensation，TCSC)的单机无限大电力系统，采用Minimax和backstepping相结合的方法，提出了一种有效的输出反馈控制方法.文献[11]将Minimax理论引入到耗散Hamilton系统中，对TCSC单机无限大电力系统，设计了干扰抑制控制器.基于上述讨论，本文将考虑多机间互电导影响存在时，多机电力系统的控制问题，并对原有Hamilton理论进行改进.运用Minimax方法对系统干扰项进行处理，通过构造与性能指标相关的检验函数，准确估计最大干扰对系统的影响，改善传统干扰处理方法[12-14]的保守性.

1 多机电力系统伪广义Hamilton模型建立

考虑多机电力系统数学模型:

(1)

其中:bi=1-(Xdi-X′di)Bii；ci=Xdi-X′di；Xdi为发电机d轴同步电抗；X′di为d轴暂态电抗；ωi为发电机角速度；ωs为发电机同步角速度；T′doi为d轴开路时间常数；Mi为发电机惯性时间常数；Di为阻尼系数；Pmi为机械功率；E′qi为q轴暂态电势；Efdsi为系统稳态运行时的励磁电压；ufi为发电机励磁输入电压；εi1和εi2为有界扰动，分别表示机械功率扰动和励磁绕组参数扰动.

选择式(2)的Hamilton函数:

(2)

将H(δ,ω,E′q)对各状态变量求一阶偏导数，可得

构造伪广义Hamilton系统:

(3)

其中，pi为状态变量x的有界映射函数，则

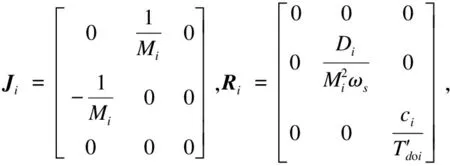
选择新的能量函数[6]:

(4)

其中，

(5)

则式(3)可以表示为

(6)

将式(6)的最后两项写成

其中,ωi包含了系统的不确定扰动项和有界向量的共同影响.可看做是新的有界扰动向量.则

则式(3)可以表示为

(7)

2 基于Minimax理论的干扰抑制控制器设计

定理1针对伪广义Hamilton系统：

(8)

若存在半正定的能量存储函数(4)和(9), 干扰抑制常数γ以及控制器(10)：

Q(x)=W,

(9)

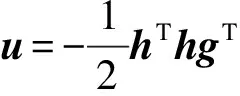
(10)

使得

(11)

则系统具有干扰抑制特性，并且在平衡点处渐进稳定.

证明：定义二次型性能指标函数:

(12)

根据Minimax理论选择检验函数:

(13)

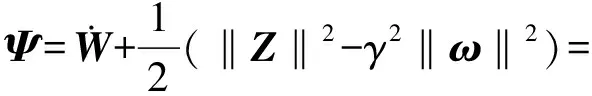
(14)

利用极值原理，对式(14)关于ω求一阶导数，并令导数等于0，可得临界干扰程度为

(15)

继续求二阶导数，可得

(16)

因此，可知干扰最大值为

(17)

(18)

如果干扰ω对系统的影响足够大，使ΔW=0，则有

(19)

此时，根据式(19)可知，ω*为对系统影响程度最大的干扰.在此干扰情况下将控制器(10)代入到式(14)中，有

Ψ=-WT·R·WT·ghThgTW+
WT·GGTWT·ghThgTW-
WT·GGTW=
-WT·R·WT·GGTW.

(20)

Q(x)=W.

(21)

则系统(8)存在半正定的能量存储函数W(x)和Q(x),使得耗散不等式(11)成立.

注1 采用Minimax理论设计干扰抑制控制器之前，先通过所构造检验函数推算出系统所能承受的最大临界干扰程度，这种干扰程度依赖于状态和系统输入的变化，而不是简单估计.

注2 根据检验函数推算系统能承受的最大干扰程度，解决了不等式放缩引起的保守性，进而准确设计干扰抑制控制器.

根据定理1，可得多机电力系统(1)发电机控制率为

(22)

对于最大破坏扰动，设计控制器：

(23)

3 仿真分析

为了验证该方法的有效性，对图1所示的三机电力系统进行仿真研究.以图中发电机节点3为参考节点，系统网络参数详见文献[1].

假定7s时发电机1和2的母线之间发生三相短路故障，7.1s时继电保护发生动作，断开故障线路，8s时故障排除，进行自动重合闸.得到仿真结果如图2所示.

从以上仿真结果可以看出，当系统在7s钟发生短路故障时扰动较大，因此，状态与稳定时平衡点状态相差较大，曲线有较大波动.当系统在8s排除故障、恢复正常工作后，控制器做出迅速调整，响应曲线能够迅速收敛于平衡点，保证了系统的稳定性.经分析，该方法可以有效抑制多机电力系统的干扰问题.

4 结 语

本文在Hamilton理论的基础上进一步改进，对多机电力系统干扰抑制问题进行了研究，并将Minimax理论与改进的Hamilton理论相结合.在处理干扰时，推算出最坏干扰程度，解决了以往对系统参数进行假设的问题，降低了保守性.通过仿真研究，说明了该方法具有有效的干扰抑制效果.