浅谈对称角的关系与应用

在角的概念推广中,经常会碰到有关对称角的关系问题。下面结合弧度制的知识,剖析常见的对称角的关系,并结合实例加以分析与应用。

一、对称角的关系

在弧度制下常见的对称角的关系如下：(1)若角α与角β的终边关于原点对称,则αβ=(2k+1)π(k∈Z)。(2)若角α与角β的终边关于x轴对称,则α+β=2kπ(k∈Z)。(3)若角α与角β的终边关于y轴对称,则α+β=(2k+1)π(k∈Z)。(4)若角α与角β的终边在一条直线上,则α-β=kπ(k∈Z)。(5)若角α与角β的终边关于直线y=x对称,则(k∈Z)。(6)若角α与角β的终边关于直线y=-x对称,则

二、对称角的应用

1.关系表示。

例1若α和β的终边关于x轴对称,则α可以用β表示为____。

解析：因为α和β的终边关于x轴对称,所以α+β=2kπ(k∈Z),那么有α=2kπ-β(k∈Z)。

2.角的求解。

例2若角α的终边与角的终边关于直线y=x对称,且α∈(-4π,4π),则α=____。

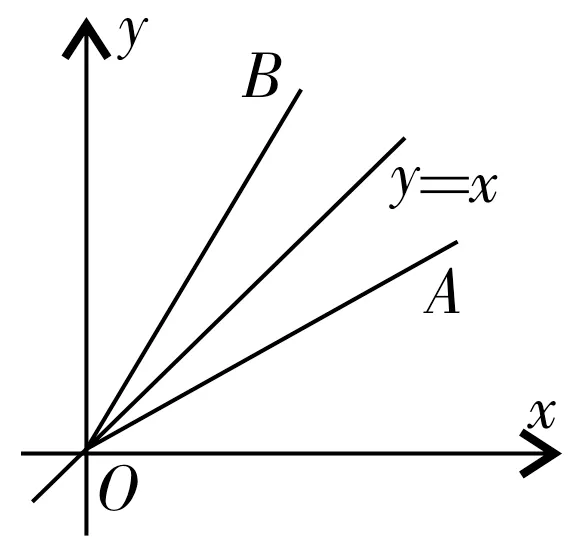
图1

解析：如图1所示,设角的终边为OA,OA关于直线y=x对称的射线为OB,则以OB为终边且在0到2π之间的角为故以OB为终边的角的集合为因 为α∈(-4π,4π),所以因为k∈Z,所以k=-2,-1,0,1。所以

3.关系式求值。

例3在平面直角坐标系中的终边与α的终边分别有如下关系时,试求β的值：(1)若角α,β的终边关于x轴对称。(2)若角α,β的终边关于y轴对称。(3)若角α,β的终边关于原点对称。(4)若角α,β的终边关于直线x+y=0对称。

解析：(1)如图2①,由于角α,β的终边关于x轴对称,则有α+β=2kπ,k∈Z,可得β=(2)如图2②,由于角α,β的终边关于y轴对称,则有α+β=(2k+1)π,k∈Z,可得(3)如图2③,由于角α,β的终边关于原点对称,则有β-α=(2k+1)π,k∈Z,可得k∈Z。(4)如图2④,由于角α,β的终边关于直线x+y=0对称,则有α+β=(2k+1)π+,可得

图2

4.三角函数值的求解。

例4已知角α与角β的终边关于y轴对称,且(α为第一象限角),求sin(α-β)的值。

解析：因为角α与角β的始边都在x轴上,终边关于y轴对称,则有β=(2k+1)πα,k∈Z。由β=(2k+1)π-α,k∈Z,得αβ=2α-(2k+1)π,k∈Z。又(α为第一象限角),所以故sin(αβ)=sin[2α-(2k+1)π]=-sin2α=-2×