直线与圆锥曲线相交过定点问题的统一性质

《数学教学》2010年10月刊登有夏新桥老师的《读刊有感——引领学生跨越思维障碍》,给出了解答问题的关键,如何利用坐标法简化解答,突破思维障碍,获得“完美”解答,读来颇是受益。笔者从该问题的另一角度思考探究,得出直线与圆锥曲线过定点问题的一些性质,并从几何特征出发获得该问题的一般解法。

原题过椭圆x2+2y2=2右焦点F的直线与椭圆相交于A,B两点,经过点B与x轴平行的直线交右准线于C点,求证：直线AC过一定点。

性质1：过椭圆右焦点F的直线与椭圆相交于A,B两点,经过点B与x轴平行的直线交右准线于B'点,F'为准线与x轴的交点,则AB'过FF'的中点。

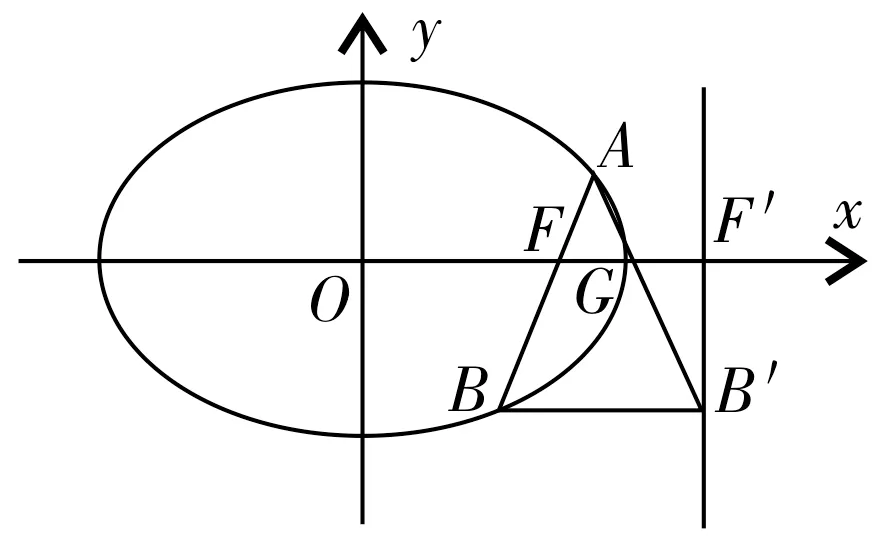
图1

证明：当AB∥l时,结论显然成立。当不平行时,如图1所示。设直线AB的方程为x=my+c,点A,B的坐标分别为A(x1,y1),B(x2,y2),则设G为FF'的中点,则有联立直线与椭圆的方程得消去x,可得b2(my+c)2+a2y2-a2b2=0,化简得(b2m2+a2)y2+2b2mcy-b4=0。所以y1+,所以kAG=,把x1=my1+c代入kAG,得kAG=kAG-kB'G=-=②。

把①代入②得kAG-kB'G=0,即kAG=kB'G,则A,B',G三点共线,所以G为AB'的中点,即AB'过FF'的中点。

圆锥曲线中椭圆具有的性质,双曲线和抛物线有吗? 经笔者认真探索,于是有：

性质2：过双曲线=1(a＞0,b＞0)右焦点F的直线与双曲线相交于A,B两点,经过点B与x轴平行的直线交右准线l：于点B',准线与x轴的交点为F',则AB'过FF'的中点。

此性质仿照性质1 的证明即可完成,此处略。

性质3：过抛物线y2=2px(p＞0)的焦点F的直线交抛物线于A,B两点,经过点B作平行于抛物线对称轴的直线AB交准线l：于点B',准线与x轴的交点为F',则AB'过FF'的中点(即为抛物线的顶点)。(证明略)