一种改进的灰色P-I-D控制算法及其在跟踪控制系统中的应用

常志英，孙立莹，佐大伟，李世荣

P-I-D 控制算法，其优点是具有控制结构不复杂、鲁棒性能不弱、可靠性不低等。但P-I-D 闭环控制算法因控制参数对控制系统效果影响大顾不适用于难以建立准确数学模型的系统，如非线性系统、时变不确定系统、时滞不确定的系统，对于实际应用中存在此类情况的系统，P-I-D 控制算法会因为参数的不确定导控制品质变低，在以误差作为基本调节项的系统出现明显偏差时微分起作用，导致系统的超调量无法在准确的时间得到有效的抑制，这种控制方法属于事后控制方法。

灰色系统：系统中存在部分明确信息已经需要进行估计的部分不明确信息（小样本）。灰色系统理论[1]——对灰色系统进行建模分析、灰色因素的关联分析、灰色预测、灰色决策、灰色系统优化的有效工具。灰色P-I-D 控制算法是以灰色系统理论为基础，通过建立灰色模型，对控制系统的需要要估计的部分不明确信息小样本进行灰色预估补偿，在一定程度上白化了控制系统的灰量，减少了对实际控制系统建模的难度，同时使P-I-D 控制算法的控制质量及其鲁棒性可以得到有效地提高。

1 跟踪控制系统设计

跟踪系统的特点是：给定量随时间变化的控制系统。系统中存在着各种扰动的影响，但提高系统的跟踪能力是主要目标，抑制扰动的影响则是次要目标。

2 跟踪系统的灰色P-I-D 控制器设计

本文对某闭环跟踪控制系统进行建模，对比以往的P-I-D 控制算法本系统应用了一种基于灰色系统理论的灰色P-I-D 控制算法。

对系统的部分不明确信息小样本（以下简称小样本）建立灰色估计模型，即对小样本进行补偿，以减小其影响并改善系统控制性能同时提高控制系统的鲁棒性，即灰色P-I-D 控制算法。其优点是：能有效地处理不确定量、需要的信息少、通用性较好、计算方便。

复合非线性不确定系统由N 个非线性不确定子系统组成：

x=Ax(t)+bu(t)+bD(x,t)

灰色P-I-D 控制算法的步骤如下：

1）第一步

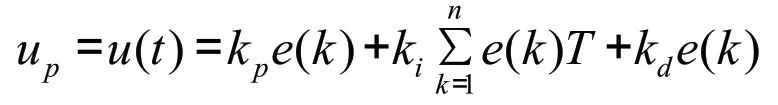
具体算法如下：

（1）建立原始的离散数列

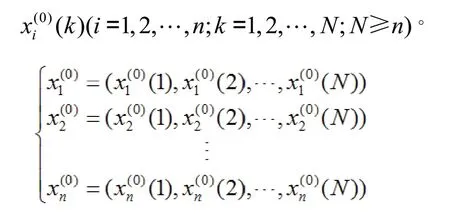
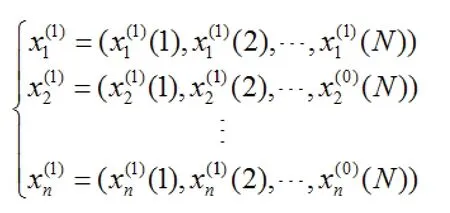
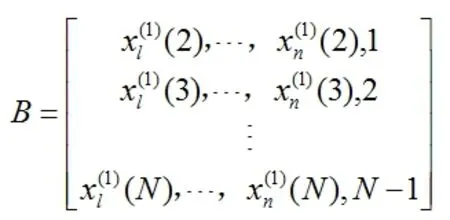
（4）计算离散序列：

D(0)(k)(k=1,2,…,N)。

D(0)(D(0)(1),D(0)(2),…,D(0)(N)T)

（5）计算1-AGO离散序列D(1)(k)(k=1,2,…,N)。

D(1)(D(1)(2),D(1)(3),…,D(1)(N)T)

（6）bD(x，t)——建模后系统的不确定部分，D(1)(x,t)——估计后的灰色模型，——灰色模型的参数向量。

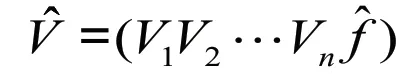
式中：f(t)为不确定周期的变扰动，控制过程中当作不变的常量进行处理，将f(t)记作f。

2）第二步

依据预估值进行补偿控制，灰色P-I-D 控制算法为

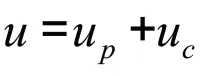
3 算法仿真分析

基于灰色P-I-D 控制算法来针对某跟踪系统进行仿真分析[2]，分析对比结果如下：

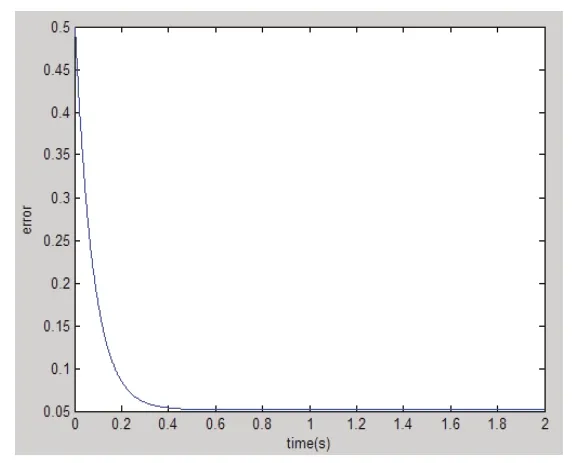
图1 灰色 P-I-D跟踪误差（M=1）

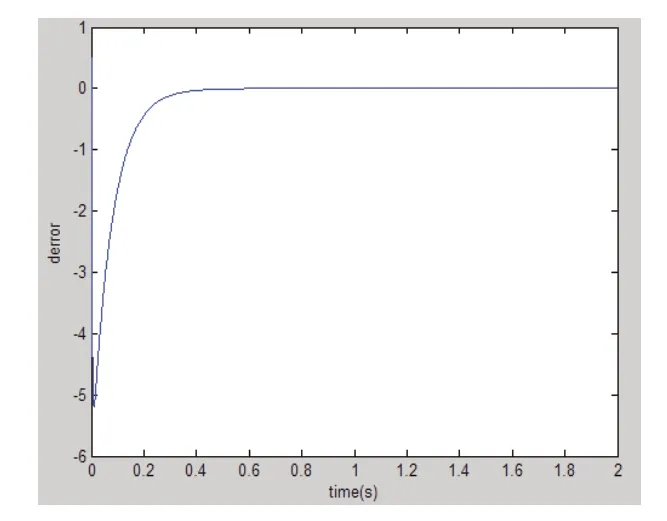
图2 灰色P-I-D跟踪误差变化率

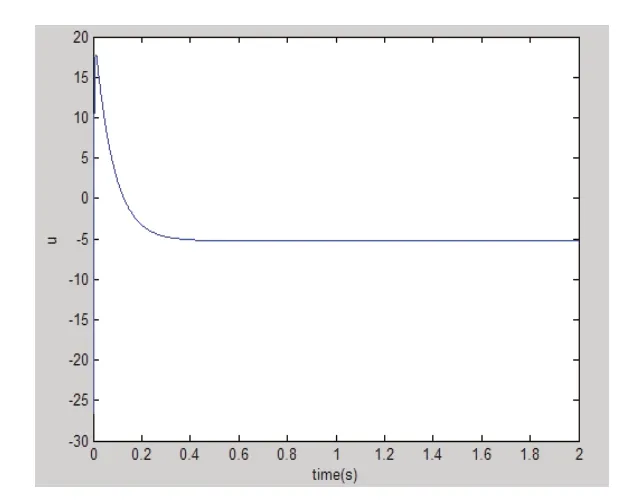
图3 灰色P-I-D控制器输出

从仿真结果来看，采用灰色补偿的P-I-D 控制算法，无论从跟踪精度还是跟踪误差方面都能快速满足系统使用要求。

4 结论

通过仿真分析结果可以确认，基于灰色理论的灰色P-I-D 算法，能快速跟踪系统变化同时闭环跟踪系统误差较小，趋于平稳时间短，超调量较小，系统抗干扰能力更强，系统动态指标更好。缺点是，系统的调节时间没有得到较好的改善，还需更进一步地研究，以使灰色P-I-D 控制在闭环跟踪控制系统的实际应用中发挥更重要的作用。