基于C4.5决策树分类算法的改进与应用

2020-05-22李春生焦海涛刘小刚

计算机技术与发展 2020年5期

李春生，焦海涛，刘澎，刘小刚

(东北石油大学计算机与信息技术学院，黑龙江大庆 163318)

0 引言

数据挖掘的过程是根据预警目标选择合适的数据挖掘算法，利用该数据挖掘算法挖掘出预警目标潜在的特征规律，根据规律特征进行目标预警。

原始数据的纯度直接关系到相关数据挖掘技术的选取，也会影响整个数据挖掘的效果。若在挖掘前的数据格式或数据类型差异很大，容易造成数据挖掘结果产生偏差，影响数据挖掘结果的准确率，无法实现科学有效的预警。同样，如果采用的数据挖掘技术不适用当前的数据特点和预警目标，容易导致算法无法发挥应有的效果，挖掘出的规律也无法用于预警。

数据挖掘算法的确立必须要以大量的历史数据和目标为依据，针对不同的数据类型和数据特点，采用不同的数据挖掘算法。不同挖掘预警目标需要与不同分析模式进行匹配，不同预警目标需要的规则表达方法也有差异。因此，有必要选择与预警目的相关的、合适度较高的数据挖掘算法。

决策树算法是数据挖掘中常用的分类与预测算法之一，其中包括ID3算法、C4.5算法、CART算法三种。文中主要针对C4.5算法，分析传统C4.5算法存在的缺点，并对其进行改进。

1 决策树方法的选定与改进

1.1 ID3算法

ID3算法是传统经典的决策树算法[1-3]，其在构造决策树时，各节点代表非类属性，边表示此时非类属性的取值情况。根据信息熵的下降速度进行属性划分，按照从根到当前节点进行路径选择测试属性，不以最大信息增益作为条件属性。ID3算法具有理论清晰易懂、使用价值强等优点，同时也存在多值偏向等问题，其运算过程通常偏重于选择属性取值较多的条件属性作为决策属性，但在大多数运算情况下，属性值取值最多的属性并非是最优属性，由于在构建决策树的过程中各个节点仅包含一个特征，也就是单变元算法，属性间不存在强相关性。也可以看成，最终生成的决策树连在一起依旧呈现分散现象。

1.2 C4.5算法

C4.5算法是基于ID3基础上的改进算法[4-7]，在一定程度上弥补了ID3算法的缺陷。C4.5算法具有可处理数据范围包含连续性数值、数据的自适用性较强、可处理不完整数据、属性选择的标准较精确以及建树完成后具有剪枝操作等优点，可避免决策树的不完整性，同时也存在生成决策树时计算效率较慢等缺点，因此最终生成决策树所表示的知识通常可采用IF-THEN形式的分类规则来表示。

1.3 CART算法

CART算法是在决策树方法基础上采用的交叉决策树算法[8-11]，具体在算法执行的过程中，首先需要选取具有最小基尼系数的属性，通过对当前决策树的节点进行分裂，选取的基尼系数越小，则表示目前拥有的训练样本集的纯度越高，采用决策树进行分类效果也就越好。CART算法主要是针对高度倾斜和多态的数值数据、有序或无序的类别型属性数据进行快速处理。该算法存在对每个节点进行多次布尔测试的诟病，按照最终的测试结果进行规则划分，当判定条件为真时判定为左分支，否则判定为右分支[12-16]。

2 C4.5决策树算法的改进

文中以C4.5算法思想在经济犯罪数据中的应用为例进行概述。运用C4.5算法的主要思想是：以训练数据集S作为样本集，当样本集S不断分裂生成经济犯罪特征决策树的同时，通过对各经济犯罪属性信息增益率的计算，选取当前数值最大的属性作为分裂节点。重复按照此标准，可将样本集S散列成n个样本子集。若在样本集分裂过程中，第i个样本子集Si内包含的元组类别相同时，当前节点可看作此时分裂决策树的叶子节点，分裂终止。若在决策树分裂过程中生成不满足上述条件的经济犯罪属性子集Si，则继续使用上述方法依次递归生成决策树，直到所有经济犯罪属性子集包含的元组均属同一个类别为止。它主要基于以下原理：

定义1：类别信息熵：假设训练样本集为S，S中有s个子样本，将此训练集划分为m个类别，第i类的实例个数可看作为Si，Pi为Si/S的概率，INFO(S)为类别信息熵，基于信息熵的计算公式为：

定义2：条件信息熵：假设A作为属性划分训练样本集S，训练样本集S被划分成k个子集{S1，S2，…，Sk}，即将A的取值分为k个{a1，a2，…，ak}，定义Si中属于第i类的训练实例个数为Sij，INFOA(S)为属性A的条件信息熵，由A划分成子集的信息熵计算公式如下：

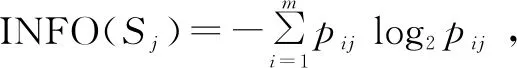
定义3：属性A的信息增益计算公式为：

Gain(A,S)=INFO(S)-INFOA(S)

定义4：分裂信息熵：设划分训练集的属性A有k个不同的值，则将属性A样本集划分为k个不同的子集。其中，样本子集Sj包含样本集S中的部分样本，ai为它们在属性A上的值。若以属性A的值为基准，对样本集进行分割，则INFO(A)表示属性A的分裂信息熵，其计算公式为：

定义5：划分属性A的信息增益率的计算公式为：

在C4.5算法构建特征决策树的过程中，选择适合分裂经济犯罪特征属性时，需要计算每个经济犯罪条件属性的信息增益率，选定信息增益率最大的条件属性作为分裂属性。由于经济犯罪涉案人特征数据量较大，需要不断计算属性的信息增益率，涉及到多次的对数运算，需要频繁调用库函数，因此增加了经济犯罪特征模式挖掘的计算量，容易产生建树效率过慢的问题。

针对上述问题，文中通过对信息增益率的计算公式进行改进，深入了解数学统计思想的泰勒公式和麦克劳林公式[17]，将二者的公式思想融入到C4.5算法的信息增益率公式计算中，从而实现信息增益率计算速度下降的目的。

由于lnx在x=0时导数无意义，且在信息增益率计算公式中常定义的概率取值范围为[0,1]，因此，选用ln(x+1)的麦克劳林公式改进传统C4.5中信息增益率的计算公式，如下所示：

于是有：

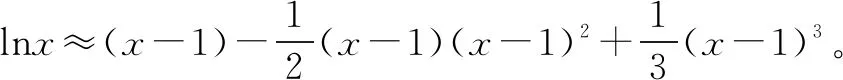
通过对以上公式进行近似简化，完全能够将对数运算转换成非对数运算，同时利用上述转化特点实现消除信息增益率公式中复杂的对数运算，从而达到简化计算过程、提升建树效率的目的。

类别信息熵的转化过程如下：

INFO(S)=

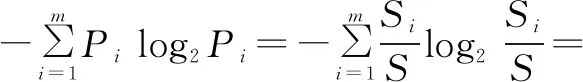
同理，条件信息熵和分裂信息熵的转化可表示为：

INFO(S)=

INFO(A)=

因此，转化后的信息增益率计算公式为：

对上述改进后的计算公式分析可得出结论，利用类别信息熵来计算条件属性信息增益率时每次的时间值相似度较高，由于上述公式在简化的过程中各部分均可省去-1/ln2S。为了有效地保证算法的分类精度，文中在计算类条件熵时采用改进的计算公式，实现不改变各个条件属性的信息增益率的排列顺序，同时又不影响分类精度。

改进后的C4.5算法与常规C4.5算法通过调用函数来进行大量的对数函数运算的不同之处在于，改进算法只需利用简单的四则混合运算，便能实现信息增益率计算公式的运算，无需多次对数运算，从而大幅提高了系统的运算速度。因此，简化后的计算公式以信息熵理论和知识为依据，在一定程度上可保留分类的精准度。

算法的主要步骤如下所示：

输入：经济犯罪数据训练样本集S，经济犯罪涉案特征属性集合list，决策属性d；

输出：决策树。

(1)以经济犯罪数据训练样本集合S作为根节点N，创建特征决策树；

(2)如果经济犯罪数据训练样本集S中的所有样本属于同一类别，则记节点N为叶子节点，并标记为类别C，否则转入步骤(3)；

(3)如果经济犯罪涉案特征属性集合list为空，记节点N为训练样本集合S中含样本数量最多的类C，否则转入步骤(4)；

(4)计算经济犯罪涉案特征属性集合list里每个条件属性的信息增益率，将具有最大的信息增益率的节点属性作为当前节点的分割属性，标记节点N为A；

(5)根据分割属性的值确定训练样本子集，并建立相应的分支；

(6)对划分出的训练样本子集重复步骤(2)～(5)，生成新的经济犯罪涉案特征决策分支，直到将所有的样本子集划分完为止。

算法流程如图1所示。

3 实验结果分析

以知识产权类经济犯罪案件作为预警目标对预警模型进行实例分析。文中采用的是数据库中的13个知识产权类经济犯罪数据集来进行数据分析，将各实验数据集分成两组，验证实验结果。将数据集分成两类，即训练样本集和测试样本集，将数据中的90%作为训练样本，10%作为测试样本。将改进后的C4.5算法命名为K-C4.5算法，文中在实验数据相同的情况下，分别对传统的C4.5算法和改进的K-C4.5算法进行对比分析，验证了改进后算法的真实有效性。在实验分析过程中，分别对传统的C4.5算法和改进后的K-C4.5算法进行准确率和时间的记录，如表1所示。

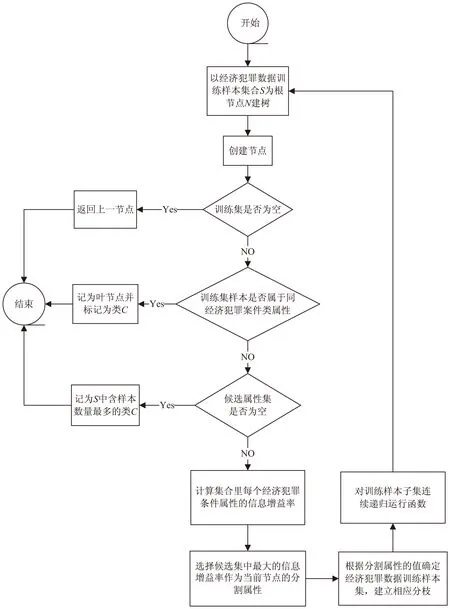
图1 算法流程

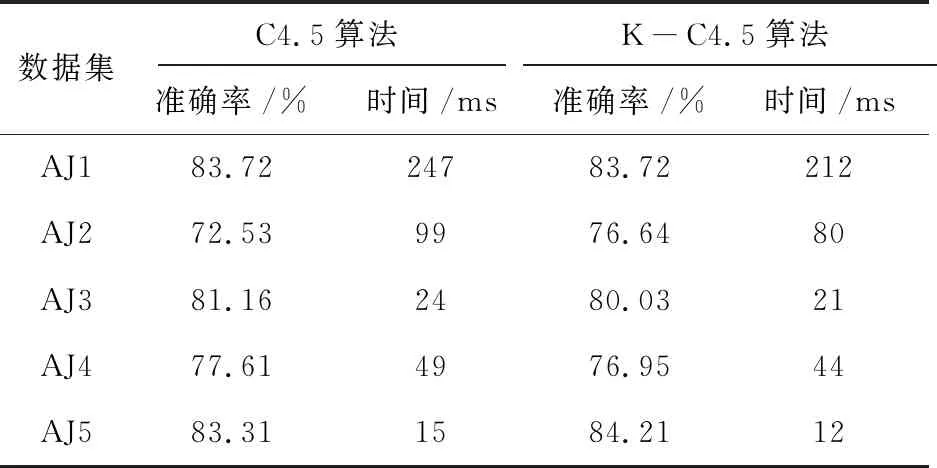
表1 算法效率统计

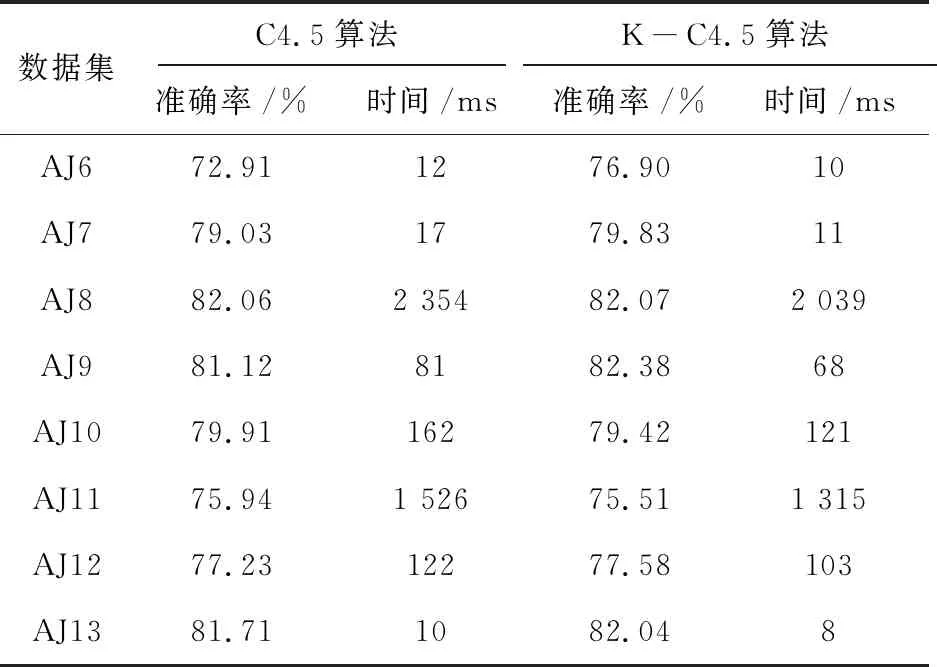
续表1

为了直观地展示算法实验结果，采用图表表示法对部分数据测试结果进行直观显示，对比分析原始的C4.5算法和改进后的K-C4.5算法的准确率和执行速度。图2是传统的C4.5算法和改进后的K-C4.5算法在分类精度上的对比，图3传统的C4.5算法和改进后的K-C4.5算法在运行时间上的对比。

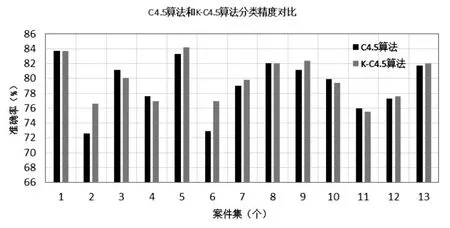
图2 算法分类精度对比

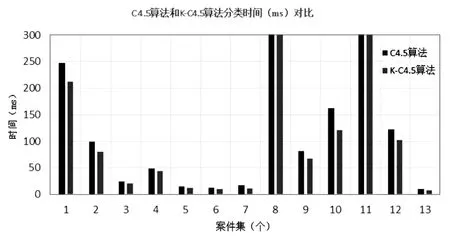
图3 算法执行时间对比

根据图2、图3的实验结果分析可得，相对于传统的C4.5算法，改进后的K-C4.5算法在进行分类时花费时间较少，同时算法时间效率提高没有影响分类的准确度，准确度与原始的C4.5算法一致性强。通过对实验结果的分析，验证了改进后的K-C4.5算法能够提升算法的执行效率，缩短算法执行时间，同时算法执行效率的提升保证了算法的准确率。