基于改进SOM模型的高校学生学习过程评价研究

马守明 郑武 程晨 周祎

摘  要：对高校学生学习过程进行准确的评价，是提升学生学习效率、改进教师教学方法、完善学校教学管理的重要环节。目前已经提出了多种数学模型来解决该问题，但这些方法均需要一定的先验知识且难以实现自学习。本文利用SOM模型能在无监督、无先验知识的状态下对样本进行自组织的特性进行学习过程的评价，同时通过主成分分析，提高了网络收敛速度和聚类准确性。实例分析表明：改进SOM模型能有效地进行学生学习过程的评价。

关键词：SOM模型;学习评价;聚类分析;主成分分析

中图分类号：TP183     文献标识码：A

Abstract： The accurate evaluation of the learning process of college students is an important link in the improvement of students' learning efficiency， teachers' teaching methods and school teaching management. The existing evaluation methods of learning process mostly rely on accurate mathematical models， which cannot realize self-learning. In this paper， the SOM （Self Organizing Maps） model was used to evaluate the learning process of samples in an unsupervised state without prior knowledge. Meanwhile， through PCA （principal component analysis） algorithm， the convergence speed and clustering accuracy of the network can be improved. The case analysis shows that the improved SOM model can effectively evaluate students' learning process.

Keywords： SOM model; learning evaluation; cluster analysis; principal component analysis

1   引言（Introduction）

高校是培养专业人才的教育机构，学生的“学”和教师的“教”构成了高校教学工作的核心环节，这也是高校实现可持续、健康发展的根基。学生的学习具有过程复杂、个体迥异、发展动态的特点，并伴随着教学活动的开展而不断动态进化[1]。探索如何对其进行科学有效地系统评价，并利用评价结果反作用于教师授课和教学管理，对高校教学质量的整体提升具有重要的现实意义[2，3]。

目前，越来越多的模拟人类智能行为或进化过程而发展起来的计算智能技术应用在学生学习过程的评价之中。文献[4]依据评价指标体系原则建立了网络学习评价指标体系，并运用模糊综合评判原理构建了一个实用的网络学习评价数学模型。文献[5]提出一种采用改进LMBP算法设计的在线评价模型，并将改进LMBP算法运用到实际在线学习的评价之中。文献[6]构建了基于BP神经网络的网络学习评价模型，并设计了基于Hadoop的BP神经网络并行算法来解决网络学习评价中的大数据集分析和处理问题。文献[7]将云模型与ANFIS结合，利用云模型代替模糊神经网络的隶属度函数，构建了ANFIS云推理网络以实现学习效果的评价。与这些方法不同的是，SOM（Self Organizing Maps）模型虽然也是一种神经网络模型，但是它是基于无监督学习的，就这使得它能够在缺乏先验知识的情况下，也能够实现对未知环境和样本空间的有效学习，从而进一步实现多指标复杂情景下的学生学习过程的分类和评价。

2   SOM模型理论（SOM model theory）

人类大脑的一百多亿神经细胞存在着广泛地自组织连接和功能分区，不同分区的神经细胞在遗传和进化的基础上，对特定的输入信号具有敏感性，从而能够对不同的感知输入形成不同的认知结果。SOM模型就是据此提出的一种自组织特征映射神经网络模型，它本质上是竞争学习型的无监督神经网络，也是应用最为广泛的自组织神经网络方法。

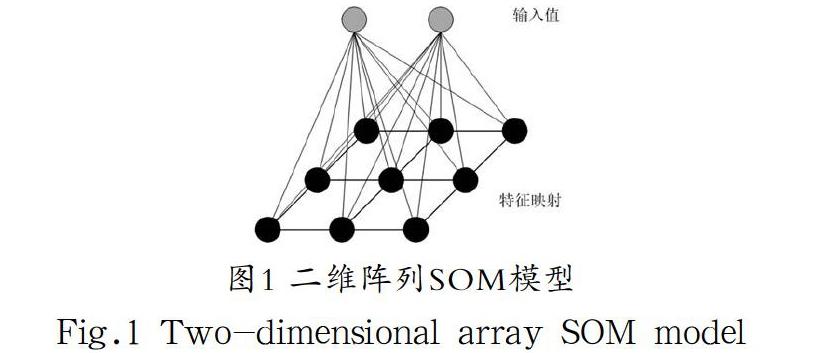
SOM模型的基本思想是认为处于空间中不同位置的人工神经元具有不同的功能分工，当接收到外界复杂的输入模式时，在输出层将会形成不同的反应区域。类似人脑，各区域对输入模式有不同的响应特性。因此，SOM模型能将高维输入数据映射到低维空间，同时还能保持输入数据在高维空间的拓扑结构，即将高维空间中相似的样本点映射到网络输出层中的邻近神经元[8]。输出层的神经元可以有一维、二维或更高维的组织形式，图1所示为最常用的二维组织形式。

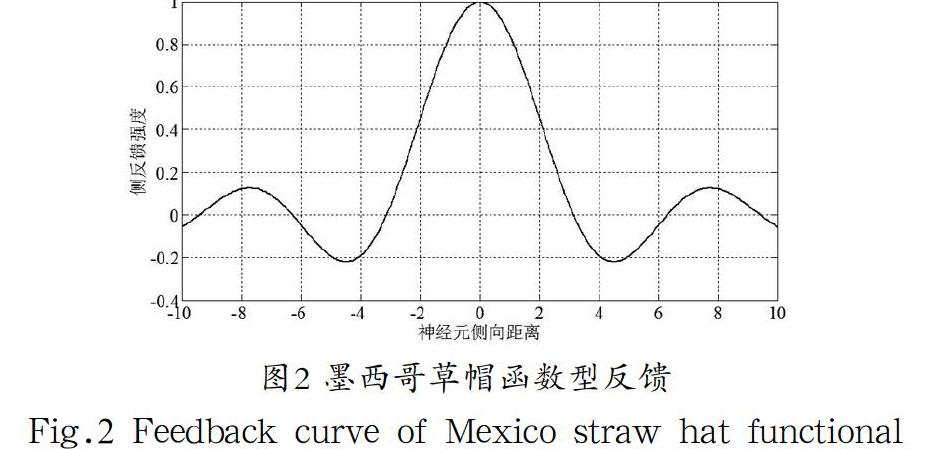
在该二维SOM模型中，输出层神经元的排列形式是矩阵结构，初始化时该层每个神经元均被赋予一个随机的权值向量。当有新样本向量輸入该模型时，通过模拟人脑神经元的侧抑制机制，每个输出层的神经元都参与竞争。例如，可以通过计算欧拉距离产生一个输入样本和权值向量之间距离最小的神经元作为获胜神经元，并同时调整其周围一定范围内邻居神经元的权值向量，该范围之外的神经元的权值向量则不进行更新。这种随着邻域距离的增加，输出层神经元之间从强化到抑制的关系转变如图2墨西哥草帽函数所示。

获胜神经元的权值调整幅度最大，距离它越远的邻域神经元调整幅度越小，当距离再远一些时，权值调整幅度为负，更远则又回到零。经过这样不断地训练与调整，最终输出层的每个神经元都能够获得维持拓扑结构的权值向量。

3  基于改进SOM模型的学习评价方法（Learning evaluation method based on improved SOM model）

3.1   SOM模型改进

在实际应用中，人们为了更全面地分析一个对象，往往会选择较多的评价指标对其进行综合描述。但由于指标的数量增多，这些指标之间难以避免地存在一定相关性，从而导致观测样本数据反映的真实信息产生重叠，甚至会影响分析结果的正确性。因此，需要用少量的不相关综合指标代替原来的大量原始指标来更有效地反映分析对象的真实情况。

SOM模型的主要优点在于其图形表示结果直观且易于理解和解释，在技术上也易于实现。但是传统SOM模型的计算复杂度较高，尤其在对数量较大、特征较多的学习数据集进行分析和挖掘时，将需要大量的计算资源和耗时，不适于时效要求较高的应用场景。为了既保持原始数据的本质特征，又能有效降低其规模，可以采用数据降维的方法。

假设原始数据元组或向量由n个属性或维度描述，在n取值较大时，如果将这些指标直接进行多元统计分析，不仅会使模型变得复杂不稳定，还有可能因为变量之间存在多重共线性引起较大的结果误差。利用主成分分析（Principal Components Analysis，PCA）搜索k（）个最能代表这些原始数据的n维正交向量可以将原始数据投影到一个小的数据空间。与属性子集选择通过保留原属性集的一个子集来减少属性集大小的思路不同，PCA通过创建综合属性指标来将原始高维数据投影到低维空间。

3.2   评价指标筛选

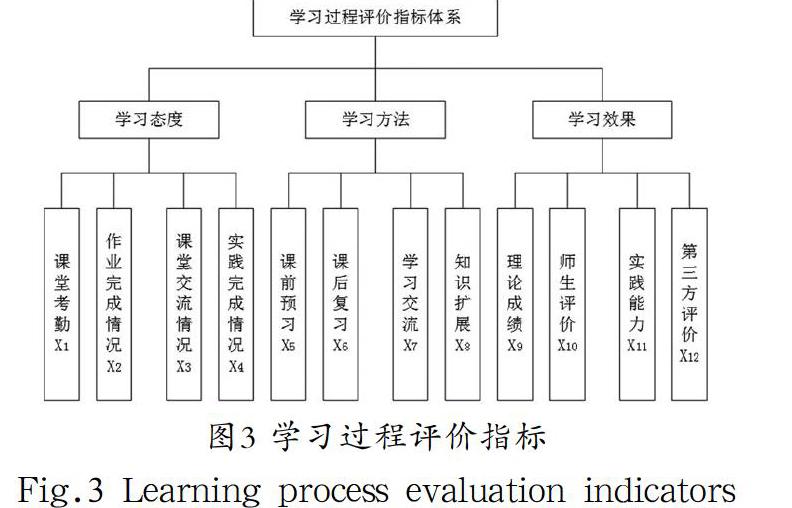
评价指标是对学生学习过程进行评价的依据，不同的评价指标会导致对同一评价对象的评价结果不同。在实际评价工作中，高校学生学习过程评价是一个多层次、多目标的复杂问题，必须根据评价目的对评价指标进行认真筛选。根据学习过程的构成，本文从学习态度、学习方法和学习效果三个方面构建包含12个指标项的评价指标体系，如图3所示。

3.3   评价方法设计

根据改进的SOM模型，本文提出的学习过程评价方法包含以下步骤：

第一阶段，进行数据预处理，基本过程如下：

（1）规范化输入的原始样本数据，避免不同属性量纲差异的影响。

（2）通过计算，求得k个标准正交向量，即为规范化输入数据的基。

（3）对主成分按重要性或强度降序排列。

（4）根据降序排列，去掉较弱的成分来归约数据。

第二阶段，建立改进SOM模型，包括以下步骤：

（1）模型初始化，主要包括权值初值和学习率初值。

（2）输入训练样本。将第一阶段生成的主成分向量输入模型。

（3）寻找竞争层获胜神经元。基本SOM模型在计算最佳匹配神经元时采用简单欧拉距离计算两个n维向量和之间的距离，数据各维分量的分布不一样。这里采用标准化欧拉距离寻找获胜神经元：

（4）进行网络权值的学习。调整获胜神经元和其邻接神经元的权值：

式中，Nc是获胜神经元的邻域，是学习因子。

（5）继续输入新的训练样本，直到学习因子逐渐下降到0或达到预定的训练轮数。

第三阶段，将待测样本输入训练好的改进SOM模型中进行可视化评价。如果该样本在竞争层的位置与某标准评价等级样本在相同位置，则可以判定它属于该评价等级。

4   实例分析（Case study）

作为基于改进SOM模型的学习过程评价方法的示例，依据12个学习过程评价指标，对85个学生样本进行百分制打分。对这些样本进行主成分分析，由样本协方差矩阵的特征向量计算可知前两个主成分的累积贡献率已经达到91.04%，故降维过程取前两个主成分，即可保证原变量信息丢失最小，且主成分个数最少以便于后续聚类分析。

选定的两个主成分的表达式如下：

这两个主成分作为改进SOM模型的输入，利用MATLAB 7.11进行仿真，将它们映射到二维神經元层。主要参数设置如下：结构函数为六角结构函数，输出层为4×4结构，排序阶段学习速率为0.9，学习步长为1000，收敛阶段学习速率为0.02，邻域距离为1。

根据具体应用场景，如果SOM模型达到训练要求就可以输出保存。当有新的样本数据输入时，SOM模型就会通过特定神经元将其进行自动分类。如果输入的样本数据不符合任何类别，则依据就近原则进行分类，这也体现了SOM模型强大的适应性。

选取五个样本数据对训练好的网络进行测试，其中，由主成分重建观测样本，可知这五个样本分类和标准分类结果是一致的，这也说明改进SOM网络模型评价具有准确性的优点，且泛化性能良好。

5   结论（Conclusion）

利用改进的SOM模型进行高校学生学习过程的聚类评价，有效减少了评价指标繁多且指标之间具有一定相关性的影响，训练过程具有无监督自学习的优点，训练结果简单直观，而且模型具有较强的泛化能力和稳定性。实例分析表明，本文方法可以为高校学生学习过程的客观、科学评价提供有力依据，从而促进高校教学工作水平的持续提升。

参考文献（References）

[1] Guri Skedsmo，Stephan Gerhard Huber.Measuring teaching quality：some key issues[J].Educational Assessment Evaluation and Accountability，2019，31（2）：1-3.

[2] Sara Mortaz Hejri，Azim Mirzazadeh，Mohammad Jalili.Peer observation of teaching for formative evaluation of faculty members[J].Medical Education，2018，52（5）：567-568.

[3] Matthew G Fete，Robert C Haight，Peter Clapp，et al.Peer Evaluation Instrument Development， Administration，and Assessment in a Team-based Learning Curriculum[J].American Journal of Pharmaceutical Education，2017，81（4）：68.

[4] 栗涛，王清心，丁家满.一种基于模糊理论的网络学习评价模型[J].山西电子技术，2009（6）：48-50.

[5] 卢宇，陈锦莹，谢静，等.基于LMBP算法的在线学习评价模式研究[J].中国远程教育，2016（3）：28-32.

[6] 陈志华.基于Hadoop的神经网络算法在网络学习评价中的应用研究[J].计算机与数字工程，2016（2）：248-251.

[7] 唐肝翌，卢桂馥，周鸣争，等.基于ANFIS云推理的网络学习评价[J].西南师范大学学报（自然科学版），2014（1）：137-141.

[8] Fangqing Gu，Yiu-Ming Cheung.Self-Organizing Map-Based Weight Design for Decomposition-Based Many-Objective Evolutionary Algorithm[J].IEEE Transactions on Evolutionary Computation，2018，22（2）：211-225.