例析“数学史”在初中数学课堂教学中的实践
2020-05-21周燚
周燚


[摘 要] 基于数学史内容常常被日常教学所忽视的现状,文章结合教学实际,以“勾股定理”为例,从融入基本教学环节、优化教材史料、利用例题习题、重视阅读材料的应用与开发四个方面具体说明数学史在课堂教学中的实践策略.
[关键词] 数学史;课堂教学;实践策略
初中教材中数学史的内容常常由于教学时间有限、史料素材有限、教师素养有限等因素被一帶而过,甚至置若罔闻. 教师如何在课堂教学中合理进行数学史教学,提高课堂效率,培养学生的数学素养以及解决问题的能力,成为亟须解决的问题. 笔者结合教学实际,以“勾股定理”的教学为例,截取教学过程中的四个片段,具体展示四种数学史的教学策略.
数学史融入基本教学环节,整合教学时间
【片段一:新课引入】
师:今天这节课我们将跟随数学家——毕达哥拉斯重走历史,共同探究有趣的发现. 毕达哥拉斯的生平如图1.
师:下面是一则关于著名数学家毕达哥拉斯的小故事.
毕达哥拉斯有一次应邀参加餐会,这位主人豪华宫殿般的餐厅铺的是正方形美丽的大理石地砖. 大餐迟迟不上桌,这位善于观察和理解的数学家便凝视脚下这些排列规则、美丽的方形瓷砖(如图2). 想到它们和“数”之间的关系,于是毕达哥拉斯拿起画笔蹲在地砖上,选了一块地砖以它的对角线为一边画了一个正方形. 他发现,这个正方形的面积恰好等于两块地砖的面积之和(如图3). 他很好奇,于是再以两块地砖拼成的矩形之对角线为一边作另一个正方形,他发现这个正方形的面积等于5块地砖的面积(如图4),也就是以两直角边为边所作的正方形面积之和. 至此,毕达哥拉斯做了大胆的假设:任何直角三角形,斜边的平方恰好等于另两边的平方之和.
说明?摇 教师提前准备史料创设情境,与引入环节相整合,带领学生重走历史,感受数学家的思考和发现,体会数学源于生活,激发学生的学习兴趣.
拓展与整合已有数学史料,优化教材史料
【片段二:勾股定理的证明】
1. 从特例出发,引导学生用面积法来证明
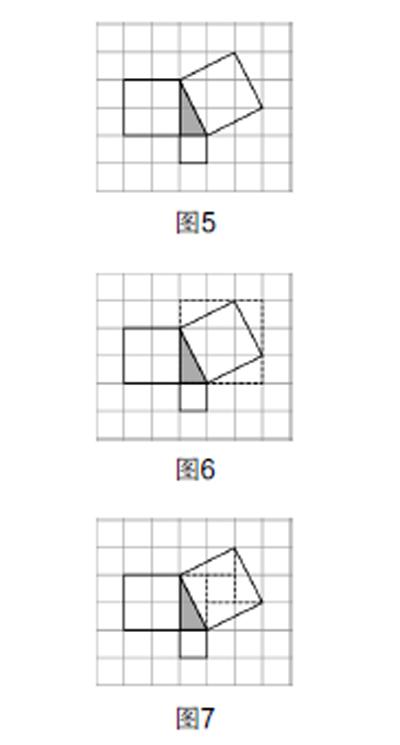
以引入中的1,2,为特例(如图5),引导学生用面积法来证明:借助网格,通过两种割补(如图6和图7),利用面积法证得猜想的结论成立.
教师总结:对于不规则图形或一个难算面积的规则图形,割补法是最常用的方法!
2. 从特殊到一般,证明a,b,c为边的情况
离开了网格,学生对边长和面积的计算都存在心理障碍,此时教师可以引导学生类比之前的证明方法,用字母表示边长,利用割补法求出大正方形的面积.
师:你们刚才证得的结论——直角三角形中两条直角边的平方和等于斜边的平方,就是著名的“勾股定理”,而大家刚才所使用的证明方法(图6所示的证法1和图7所示的证法2一般化后,证法1如图8,证法2如图9)也和历史上伟大的数学家不谋而合. 我们的证法1,相传是伟大数学家毕达哥拉斯于公元前550年首先证明的(如图10);证法2则是我国著名数学家赵爽所发现的方法,该图案同时也成为2002年在北京召开的第24届国际数学家大会会徽图案(如图11). 可见,勾股定理在数学史上有着十分重要的地位.
说明?摇 两种勾股定理的证明方法可完全由学生探究得到,让学生重走数学家的探究路径,和数学家一样研究数学. 数学史在帮助学生了解和掌握更多解决问题的思路方面有着不可替代的作用,其中证法2在教材中有相应的数学史料(浙教版《义务教育教科书·数学》八年级上册P76课后设计题,如图12),而证法1对应的数学史料就需要教师自己查找补充. 这样的资料收集具有方向性,可操作性强,这样逐步积累与整合史料,便能慢慢完善适合教学的数学史资料.
教师可再整理几种具有代表性的证明方法印制资料发给学生,供学生比较、探究. 通过了解证明方法的产生过程,学生能体会到一些真实的数学思维,对一些数学问题能形成更深刻的认识,从而在这种不断学习、不断探索、不断研究的过程中逐步培养创新能力.
师:勾股定理在数学史上还有很多别称呢!例如,毕达哥拉斯定理、商高定理、百牛定理、驴桥定理和埃及三角形等. 这个定理的历史十分悠久,几乎所有文明古国(古希腊、中国、古埃及、古巴比伦、古印度)对此定理都有研究. 下面将历史上其他具有代表性的证明方法的资料发给同学们,这样我们就可以和数学大家们一起来研究了.
资料
方法1:欧几里得证法(北师大版《义务教育教科书·数学》八年级下P17)
著名的古希腊数学家欧几里得在巨著《几何原本》中给出一个很好的证明. (图13为欧几里得和他的证明图)
方法2:刘徽的证法(资料源于网络)
刘徽在《九章算术》中对勾股定理的证明:勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不移动也,合成弦方之幂,开方除之,即弦也. (如图14的青朱出入图)
方法3:总统证法(人教版《义务教育教科书·数学》八年级下P30)
美国第二十任总统詹姆斯·加菲尔德的证法在数学史上被传为佳话,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法(如图15).
方法4:婆什迦罗证明法(资料源于网络)
印度数学家兼天文学家婆什迦罗对勾股定理给出了一种奇妙的证明,也是一种分割型的证明. 如图16,把斜边上的正方形划分为五部分,其中四部分都是与给定的直角三角形全等的三角形;一部分为以两直角边之差为边长的小正方形. 很容易把这五部分重新拼凑在一起,得到两个直角边上的正方形之和.
师:勾股定理的证明方法还有很多,大家课后可以自己查阅资料再找几种并进行比较,希望大家能够从中梳理出一些解决问题的基本思想方法,帮助大家更好地学习数学.
说明?摇 我们在学习数学知识的过程中,若能还原历史上那些数学家们对同一个问题的研究路径和解决方法,一方面能让学生感受智力的挑战,体会成功,另一方面,通过比较、分析各种方法,能加深学生对数学知识的理解. 勾股定理的证明方法有面积证法、弦图证法、比例证法等300余种. 通过搜索、比较数学史上的各种不同方法,不仅能让学生更好地领会每種方法的本质,而且能启发学生通过分析、比较,咀嚼出数学思想方法.
合理利用、渗透数学史的例题和习题,培养教师素养
【片段三:例题教学】
浙教版《义务教育教科书·数学》八年级上册课后作业题第六题如下.
《九章算术》中记载了一道有趣的数学题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何?”
(根据实际需要给出翻译和示意图)
翻译:有一边长为一丈的正方形水池,在池中央长着一根芦苇,芦苇露出水面一尺,将芦苇拉到池边的中点处,芦苇顶端恰好达到水面,问水有多深,芦苇有多长. (1丈=10尺)
数学问题:如图17,AB=10,G为AB的中点,EF⊥AB,FG=1,EF=BE,求BC和BE的长.
(学生解答过程略)
师:古人也是这样解决问题的,因此方程思想也是从古至今沿用的,数学的历史就是数学发展的过程,一脉相承.
说明?摇 教材选用《九章算术》中的一道应用题,学生在学有所用的同时能够了解中国古代的数学成就. 教师在分析题目的过程中,应着重将文字语言转化为数学语言,将实际问题转化为数学问题,在问题解决的过程中渗透方程思想,培养学生的数学应用意识和数学建模思想.
历史名题中蕴含了丰富的思想方法,从古至今一脉相承,能让学生感到数学的有趣和有用,能让学生更加重视和发展数学应用能力,能提高学生应用数学的自觉性,从而增强学生解决问题的能力.
合理利用含有数学史知识的例题、习题,需要教师事先查阅资料了解历史,补充一些背景知识与解题方法,这无形中也培养了教师的人文素养.
重视渗透数学史的阅读材料的应用与再开发,提高教师能力
【片段四:阅读材料】
师:(浙教版《义务教育教科书·数学》八年级上册P78阅读材料)在欧几里得时代,《几何原本》第六卷命题31曾经介绍:“在一个直角三角形中,在斜边上所画的任何图形的面积,等于在两条直角边上所画的与其相似的图形的面积之和. ”(教师解释“相似”的含义)同学们可以自己思考一下这个命题,并加以证明.
(学生小组讨论,有图18、图19、图20三种情况,逐一汇报,得出结论)
师:通过以上汇报,我们用三个实例说明以上命题是成立的,那其他正多边形呢?其他相似的几何图形呢?大家课后继续探究!
变式拓展 ?摇条件同图20,但改为向内作图呢?如图21,三块阴影的面积分别记作S1,S2,S3,结论一致吗?
(师生共同解决以上问题)
师:其实这种变式也有相应的史料佐证. 公元前约400年,古希腊的希波克拉底研究了他自己所画的形如图21的图形,得出如下结论:“两个月牙形的面积之和,等于△ABC的面积,即S+S=S.”
师:那图18与图19是否也有以上变式?大家动手试一试!
分析?摇 教材中出现频率最高的数学史料就是课后的“阅读材料”,合理运用这些材料进行拓展变式,往往事半功倍. 从史料中的命题入手,引发学生的探究兴趣,将问题开放化,通过学生的自主探究将原本如图18、图19、图20的三种常见图形自然呈现,符合知识的形成规律. 另外,及时变式拓展:(1)改变图形的形状进一步探究,结论不发生变化;(2)改变以斜边为边形成的图形的方向,相应结论发生改变. 层层递进的探究,使学生体会到以“勾股定理”为核心可以发生多角度的变化,但是万变不离其宗. 通过这层层深入的探究,能培养学生的创新能力,同时,其思考问题的能力、解决问题的能力也能得到拓展、提升.
立足于教材,以“阅读材料”形式呈现的数学史资料,选取与练习相结合的点进行再开发、再拓展,既传承了数学一贯的延续,又在教学中得到发展与延伸,还培养了教师的联系与整合能力.
结语
一位学者说过:“数学是一种文化,回归源头能使我们获得对思想过程的重要认识,更加清晰地理解现在的问题. ”数学史教学的重要性不仅是为了激发学习兴趣等外在原因,主要是把数学发展中同时期和不同时期的数学文化联系起来,使数学史成为支持教与学的重要组成部分. 同时期的数学文化含有课堂对话和课堂活动的自然情境,不同时期的数学文化则联系着数学的发展. 学生在一定的社会文化背景下掌握数学知识的构建意义、思维模式以及发生发展形式,不仅实现了数学认知的发展,更重要的是实现了数学元认知的发展. 数学史渗透于教学的发展方向是积极的,虽然在实施过程中存在很多阻碍因素,但只要教师和学生认识到其对于数学教与学的作用和价值,并有意识地应用于实践,相信还是能发现很多有效的方法和途径. 其最终目标是培养学生掌握更多更好的方法,以进一步认识数学、研究数学.
