全息凹面光栅光谱仪信号复原技术研究

(南京邮电大学 自动化学院, 南京 210000)

分辨率在光谱仪器中是非常重要的一项技术指标，它直接影响着仪器的分析能力。光谱仪的分辨率主要是由其使用的硬件所决定，如狭缝线宽，准直镜口径，光栅刻线密度，光栅口径等等[1]。分辨率不足会导致光谱信号发生混叠难以分辨，光谱信号复原技术则是一种能够在一定程度上提高仪器分辨能力的数学方法[2]。

通常，光谱信号复原需要获知仪器的光谱响应函数作为一种先验信息，为了获取仪器的光谱响应函数，常用的方法有直接计算法和测量法，计算法需要获得仪器的设计参数，再利用光学衍射方程来求解光谱响应函数的近似解，这种方法虽然可以直接通过计算得到仪器的响应函数，但是对于大多数商用仪器来说仪器的设计参数是商业秘密通常不会公开，且由于系统中的各种误差影响，计算得到的结果往往和实际值存在偏差。

相比较计算法，测量法是使用一些能产生窄线宽光谱的光源作为输入光源，直接测量得到光谱冲击响应曲线，但直接测量得到的结果中包含有各类噪声不能直接作为先验信息，因此需要进行曲线拟合从中提取得到较为可靠的解。曲线的拟合都需要以某种数学模型为对象，目前市场上大部分光谱仪多采用Czerny-Turner结构，此光谱仪的像差校正比通常较为完善，因此仪器的冲击响应曲线可以被高斯曲线很好的近似[3-5]。全息凹面光栅光谱仪的成像离轴角度较大，成像系统存在着较大的慧差[1，6，7]，实验发现全息凹面光栅光谱仪的光谱响曲线向一侧发生倾斜，左右并不对称，而高斯模型则是一种典型的左右对称模型，直接使用高斯模型提取仪器响应函数必然是无法得到准确结果的。

针对这个问题，本研究提出了一种基于全息凹面光栅光谱仪光谱响应曲线的改进模型，利用改进模型拟合提取出的结果作为算法的先验信息输入，利用基于泊松随机场的反卷积算法完成全息凹面光栅光谱仪的信号复原。

1 全息凹面光栅光谱仪点扩散函数模型

全息凹面光栅光谱仪中产生色散的元件是全息凹面光栅，光源发出的光线由狭缝进入仪器照射在全息凹面光栅上发生色散并聚焦，最终成像于探测器阵列上。

光谱仪的点扩散函数是狭缝衍射，光栅衍射和光学系统综合像差共同作用的结果，进而可以被概括为如下的卷积表达式(1)。

hobservation=hslit*hgrating*haberration(1)

其中*为卷积运算符号。hslit为狭缝衍射卷积函数，具体形式如式(2)，ω为狭缝宽度，f2为成像焦距，λ为入射光波长，x为像面位置。

(2)

式(3)为hgrating为光栅衍射卷积函数，其中ωg为光栅刻槽宽度，d为光栅常数，N为光栅刻线数。

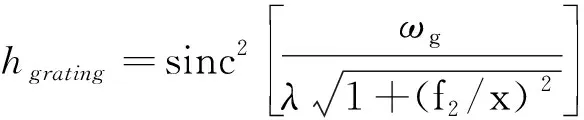
(3)

式(4)haberration为光学系统综合像差卷积函数可近似为

haberration≈exp(-a(λ)x2)

(4)

在实际工程中为了简化计算，通常将光谱仪中的hobservation函数的最终形式近似为高斯函数[8，9]。

对于全息凹面光栅光谱仪，综合像差卷积函数需要被被分解为离焦hdefocus和慧差hcoma两部分,虽然hdefocu通常可以被近似为一个高斯函数，但hcoma却比较特殊，因为慧差对光强能量分布的影响类似于彗星，实际慧差所形成的光强分布的理论公式极为复杂且繁琐非常不利于处理计算，出于方便实际数据处理和减小计算量的考虑，工程上需要寻找一种简化的同时又能很好的反映慧差特性的函数。从Namioka T , Seya M等人发表的关于全息凹面光栅的文献中发现，该类光栅谱线表现出的光强分布特点是在某一点处光强很强，再从该点开始向某一侧光强急剧减小而另一侧光强则为零[6，7]，根据这一特性同时为了简化计算起见，本文将hcoma近似为一侧区间上的指数函数，如式(5)。

hcoma≈exp(-b(λ)x)；x≥0

(5)

综上全息凹面光栅光谱仪的点扩散函数的简化模型可写成式(6)

hobservation=hGaussian*hcoma

(6)

hGaussian=exp(-c(λ)x2)

(7)

hcoma=exp(-b(λ)x)；x≥0

(8)

因此最终的拟合式如式(9)

h=d(f*g)+c

(9)

(10)

(11)

其中常数项c用来描述传感器中的底噪的期望值，d是幅值。

2 基于泊松随机场的反卷积算法介绍

在光学成像系统中，图形中的噪声常常呈现出泊松分布的形式，而一个随机变量X具有泊松分布，指的是其取整数k的概率可以被式(12)所表达

(12)

其中λ是X的期望。

因为光谱仪得到的数据是一行数组，所以可以用x和y来描述整个光谱仪输入和输出图形，xn和yn表示对应像素点的值，则光谱仪的系统模型可以表示为式(13)。

(13)

其中hi表示仪器点扩散函，vi表示对应像素点的噪声。而在无噪声情况下的系统期望信号可由式(14)给出。

(14)

则在给定原图形为x而实际观测为y，系统噪声模型为泊松模型下的概率分布式(15)

(15)

该式为泊松分布似然函数，可以利用最大似然估计原图形x。对其两边取对数可得最大似然估计式(16)。

(16)

为求P的极大值，继续求p对x的偏导，并令结果为0，得式(17)。

(17)

因为对点扩散函数h求和结果恒为1，故进一步有式(18)

(18)

对其使用迭代法，可得x的最终迭代式(19)[9-11]。

(19)

3 实验结果

3.1 光谱响应曲线拟合结果

实验使用GP3HG-1低压汞灯和一台自行研制的全息凹面光栅光谱仪工程样机进行，该汞灯可以产生自然展宽远小于仪器极限分辨率的窄带光谱[12]，以此作为仪器的激励信号，测量全息凹面光栅光谱仪的响应，本研究提取了汞灯谱线中分布较为独立并且信噪比较高的几个波长，分别进行归一化，如图1所示。 从图中可以看出系统的实测信号中覆盖有一层底噪其为系统的暗电流噪声，暗电流噪声是传感器所固有的一种电噪声其期望值为一常量，因此需要在拟合模型中加入一个常数项作为其期望值，并在拟合过后去除这个常数项。

图1 归一化并对齐谱峰后的8个波长的响应曲线

首先对测得的几个波长谱线归一化结果求取均值，再利用改进模型对其进行最小二乘拟合，再减去拟合式(11)中用来描述暗电流噪声的常数项c，并令幅度值d等于1后就可以得到估计的仪器点扩散函数如图2所示。图3则为高斯模型直接拟合的结果，观察图2和图3相比较图1，从直观上已经能看出改进模型能更好的反映仪器的响应特征。

图2 改进模型拟合的光谱仪点扩散函数

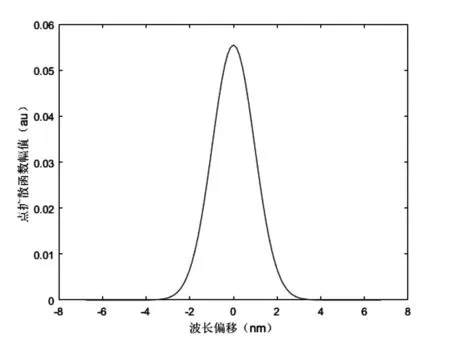
图3 高斯模型拟合的光谱仪点扩散函数

表1给出了两者模型的客观拟合效果，通过表1可知改进模型对比高斯模型在残差平方和，均方根误差，R方系数等评价拟合效果的关键指标上都有了显著的提高。因此本研究所提出的改进模型相比较高斯模型能更好的描述全息凹面光栅光谱仪的光谱冲击响应曲线。

表1 两种模型的拟合效果评价

3.2 改进模型的光谱复原结果

为了进一步地验证改进模型对全息凹面光栅光谱仪信号复原的效果，继续使用GP3HG-1低压汞灯作为全息凹面光栅光谱仪的测试光源。分别用高斯模型拟合出的点扩散函数和改进模型拟合出的点扩散函数作为算法的先验信息，算法迭代次数均设为20次[13]，并与实测信号进行对比。实测信号为实际光谱分析中较为有代表性的两种情况，分别为对称光谱双峰和不对称光谱双峰，第一组为峰值在2065像素点和2081像素点的，576.96nm和579.07nm波长对称光谱双峰如图4，第二组为峰值在2419像素点和2427像素点的，625.20nm和626.20nm波长不对称光谱双峰如图5，半高全宽(FWHM)均为1.37nm，两组信号都受到了仪器分辨能力的限制发生了一定程度的光谱重叠。

复原效果的评价主要依据为复原过后光谱的半高全宽(FWHM)和复原后光谱谱峰的对应波长位置相比较真实值的改变量[14，15]。

图4 对称光谱双峰复原效果

图5 不对称光谱双峰复原效果

结合图4和图5和表2，可以明显看出以改进模型拟合出的点扩散函数作为先验信息的复原结果，在对称光谱双峰的例子中，谱线半高全宽和光谱波长定位准确度上都比高斯模型有了明显的提高。而在不对称光谱双峰的例子中，改进模型的半高全宽依旧要优于高斯模型，但值得注意的是，在高斯模型下不对称双峰复原的结果中丢失了625.20nm的光谱曲线，这是由于高斯模型本身并不能准确的描述仪器响应所致，因所提供的先验信息不准确，进而在复原过程中出现了较为严重的错误，复原结果也完全失去了参考的价值。改进模型下的复原结果则不存在这种情况，复原的光谱中保留了所有光谱特征信息。 总得来说改进模型相比较传统仪器中常用的高斯模型，能够更好的反映出全息凹面光栅光谱仪的光谱响应曲线，利用改进模型得到的仪器响应函数做为光谱信号复原算法先验信息输入，更具有有效性和正确性。

表2 两种模型对应两种类型光谱双峰复原结果

/表示不存在

4 结论

针对传统光谱仪中常用的高斯模型存在的不足，本文提出了一种基于全息凹面光栅光谱仪的光谱响应曲线改进模型，利用低压汞灯产生的脉冲光谱测得了一台全息凹面光栅光谱仪的实际光谱响应，并分别利用本文提出的改进模型和传统高斯模型，提取了仪器的光谱响应函数，并作为输入光谱信号复原算法的先验信息分别测试实际光谱信号复原效果，实验结果表明在全息凹面光栅光谱仪中改进模型相对于高斯模型更加有效。