基于Markov模型的零部件标准规格推荐方法研究

方喜峰，王 俊，朱成顺，李伟伟

（1.江苏科技大学机械工程学院，江苏 镇江 212003；2.江苏省船海机械装备先进制造重点实验室，江苏 镇江 212003）

1 引言

随着现代市场竞争日趋激烈，企业之间的竞争开始基于时代和竞争的基础上，转变为以客户需求为基础的竞争，为客户提供定制产品，全面提高客户满意度已经成为现代企业发展的必然趋势[1]。大规模定制生产模式将定制生产和大规模生产有机的结合，在先进制造技术和柔性技术下，根据用户的个性化需求，在大规模定制生产的成本和速度的基础上，为用户提供定制产品和服务[2-3]。正是大规模定制这种独特优势引起了国内外研究学者的关注。文献[4]认为模块化是实现大规模定制的重要组成部分。文献[5]将柔性生产引入大规模定制中，应用模块化方法构建了柔性的生产计划体系结构，满足大规模定制下产品多样化的需求。

标准化在大规模定制的发展历程中起着至关重要的作用。通过标准化，企业可以在已有产品结构的基础上进行产品的创新，减轻设计人员的工作量，将设计人员的精工作力投入产品创新部分的研究中，有利于资源的充分利用，提高设计效率，降低设计成本，缩短产品的开发周期[6]。而标准件的零部件规格又是企业标准化中不可或缺的。由于目前制造企业普遍都是根据相关的设计数据找到已有的参数组合，并以此作为标准规格进行推荐。如果能通过发掘数据内部的规律，找到设计数据中并不含有的参数组合，并将其作为标准规格进行推荐，可以丰富企业设计人员的选择性。因此，将Markov模型引入企业零部件标准规格推荐中，因其可以发掘参数组合的内在关系，从而得到先前并不含有的参数组合关系，有效提高了零部件标准规格推荐效率。

2 数学模型

2.1 Markov模型简介及相关研究

马尔科夫模型[7]是马尔科夫过程的模型化，于1870由俄国数学家markov提出，他把发展过程看作一系列状态的不断转移。转换为数学表示：时刻t的状态用Q（t）表示，它可以是n种状态集合S=［S1，S2，…，Sn］中的任意一个。通过‘转移概率’可以表示马尔科夫模型的特征，即后一状态出现的概率取决于其前面状态所出现的顺序。

状态Q（t）出现的概率为：

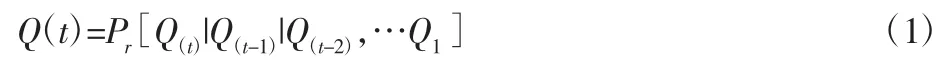
马尔科夫模型的应用非常广泛。通过研究离散现象的发展过程，统计出来状态变化的规律，预测出下一步可能要发生的事情。文献[8]把马尔科夫模型引入汉语语句相似度计算中，以关系向量为基础，利用汉语相似性特征，对权重值进行加权处理，实现了语句相似度计算，大大提高了在检索标题相关新闻的准确率。文献[9]将马尔科夫模型引入船舶设备可靠性分析中，基于马尔科夫模型建立了船舶设备复杂系统的多态可靠性模型，推导了在封闭形势时，变状态概率微分解算方程，给出了可用度、期望性能输出和期望性能失效等可靠性度量参数分析方法。此外，马尔科夫模型还被广泛应用在环境保护以及信息安全等领域。

2.2 N-1阶Markov模型

假定S表示某一个序列，是由一定顺序的词汇W1，W2，…，Wn组成，其中下标n表示序列的长度。若想知道这个特定序列S出现的可能性，即数学上所说S的概率P（S）。通过条件概率的计算公式，序列S出现的概率等于序列中每个词汇出现的条件概率相乘，于是P（W1，W2，…，Wn）可展开为：

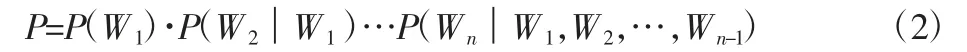
其中P（W1）表示第一个词汇W1出现的概率；P（W2|W1）是在已知第一个词汇的条件下，第二个词汇出现的几率；依次类推。从公式（2）中我们可以发现，词汇Wn出现的概率取决于它前面的所有词汇出现的顺序。

从计算量可以发现，第一个词汇P（W1）与第二个词汇P（W2│W1）的计算都比较容易，而在已知第一个和第二个词汇的条件下，第三个词汇条件概率P（W3│W1，W2）的计算难度就大大增加了，因为它涉及到三个变量W1，W2，W3。至于最后一个词汇Wn，条件概率P（Wn│W1，W2，…，Wn-1）的计算就更为复杂了。

假设某个词汇Wi出现的概率只与前一个词汇相关，那么计算难度就大大简化了。此时序列S出现的概率就变为：

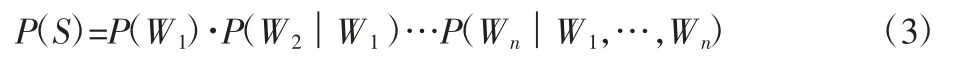
式（3）这种假设被称为N阶Markov模型。

假定序列中的每个词汇Wi和前面的N-1个词汇有关，而与更前面的词汇无关，此时，词汇Wi的概率只取决于前面N-1个词汇P（Wi-N+1，Wi-N+2，…，Wi-1）。因此：

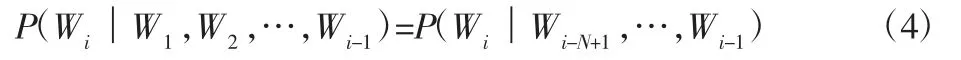
式（4）的这种假设被称为N-1阶Markov模型，对应的模型称为N元模型。

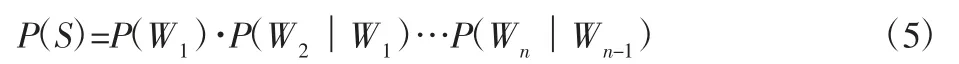
式（5）就是N=2时的Markov模型，即二元模型。一元模型（N=1）是指词汇Wi与其前面词汇无关的模型，在实际应用中，大多使用N=2或者N=3的模型，更高阶的模型就很少使用。

3 基于Markov模型的零部件标准规格推荐方法

在现代机械产品的设计中，为提高企业产品的设计效率，实现产品的快捷优化设计，越来越多的零部件产品采用参数化设计[10]。参数化设计是指零件或部件的形状比较固定时，将模型的特征尺寸设置为可以任意调整的参数，通过修改参数值来驱动生成不同的形状或尺寸的零部件[11]。设计人员可以在遵循原设计意图的基础上，对已有模型参数进行修改，从而生成系列产品，大大提高了企业的设计效率。

参数化零部件中有着大量不同参数，参数之间有着紧密的联系，一旦参数及参数值的使用次数及频率达到一定数量之后，此参数值就可以成为参数化零部件中的一种标准规格。因而，一个参数化零部件有很多标准规格。如果能发掘参数化零部件中数据内部的规律，找到隐含的参数组合，也可作为标准规格进行推荐。因此，通过对Markov模型的相关理论知识和应用进行研究，提出了基于Markov模型的零部件标准推荐方法，提高企业推荐方法的工作效率，降低出错率。

基于Markov模型的零部件标准规格推荐方法步骤流程图，如图1所示。

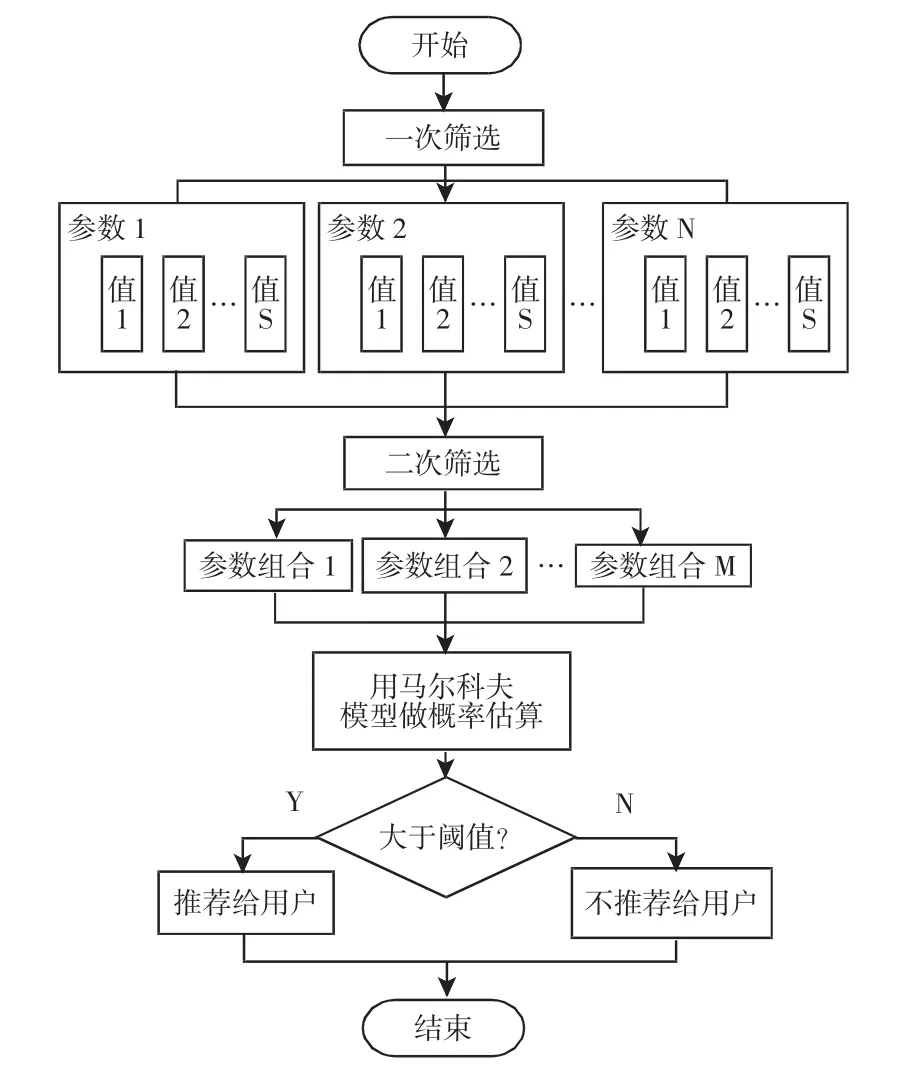
图1 标准规格推荐方法步骤流程图Fig.1 Standard Specifications Recommended Method Steps Flow Chart

具体步骤如下：

（1）一次筛选，筛选出含有相同参数的零部件图纸；将其存入M×N（M为图纸数量，N为参数个数）的二维矩阵中，该矩阵表示方式如下：

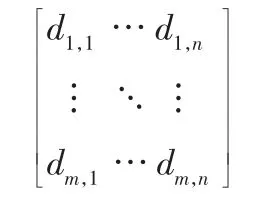
该矩阵的列向量为每张图纸在该参数中的数值，其矩阵的行向量为每张图纸中所拥有的参数值。

（2）筛选出的图纸集中，将所有的参数值进行聚合处理，并将处理后的结果存入堆栈，利用聚合后的参数值，分别计算每个参数值的概率；即，其中Pi表示参数值，#表示参数集合。

（3）二次筛选，筛选同类参数值出现概率最高的前m个参数值；即MaxN=m（P（P1），P（P2），…P（Pn）），其中P（P1）是指参数值等于P1时的概率，依次类推，P（Pn）是指参数值等于Pn时的概率。

（4）对筛选出的参数，将其参数值之间做笛卡尔乘积，得到一系列参数组合；例如：集合A=｛x，y｝，集合B=｛a，b，c｝，则两个集合的笛卡尔积为｛（x，a），（x，b），（x，c），（y，a），（y，b），（y，c）｝。

（5）求每一个参数组合出现的概率；即：P（S）=P（P1）·P（P2），…P（Pn）。

（6）筛选出出现概率最高的M个组合；M的取值，系统中会有一个初始值，用户可以根据自己的实际需求进行调整。这里以M=1为例，即筛选出概率最大的参数组合，相关伪代码如下：

（7）利用N-1阶Markov模型对每一个组合估算其出现的概率；即：

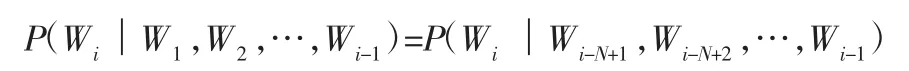
（8）将条件概率大于阈值的参数组合作为标准规格推荐给用户。

4 算法验证与讨论

鉴于国内尚无将Markov模型引入零部件标准规格推荐中，为验证算法的可行性，按照上文所述的方法步骤，以某企业船用柴油机机架为例，模型，如图2所示。

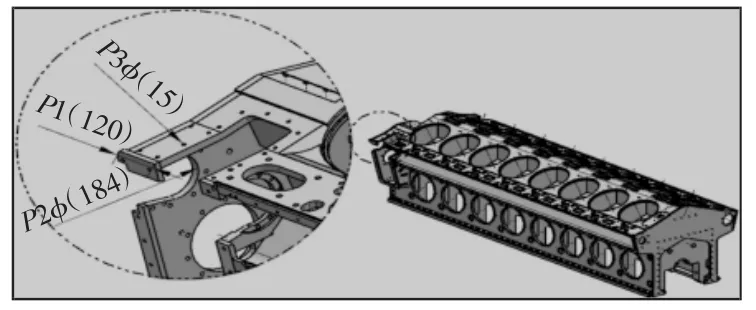
图2 某企业船用柴油机机架Fig.2 An Enterprise Marine Diesel Engine Frame

来详细说明基于Markov模型的零部件标准方法，步骤如下：

（1）一次筛选

①筛选出含有相同参数的零部件图纸，并列出图纸中各参数的值，如表1所示。

②在筛选出的图纸集中，将所有参数值进行聚合处理，并将处理后的结果存入堆栈，利用聚合后的参数值，分别计算每个参数值的概率。

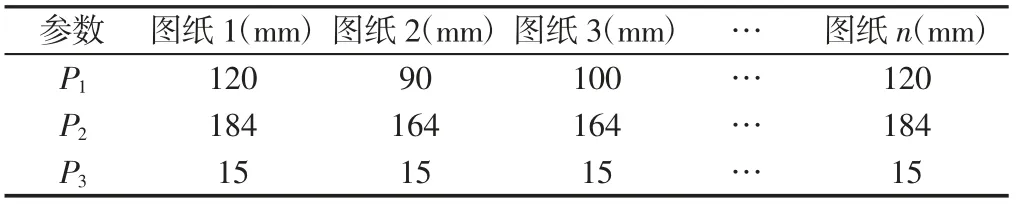
表1 相同参数零部件图纸Tab.1 Draw ings of Parts w ith the Same Parameters

（2）二次筛选

①筛选同类参数值出现概率最高的前N个参数值。N的取值，在系统中有一个初始值，也可以手动设定。这里以参数个数P=3为例，在聚合后的参数集中，参数P1取值概率最大的分别为P1=120，P1=90，P1=100这3个取值；参数P2取值概率最大的分别为P2=184，P2=164，P2=170；参数P3取值只有P3=15。筛选的结果，如表2所示。

表2 概率最高的三个参数Tab.2 Three Parameters w ith the Highest Probability

②对筛选出的参数，将其参数值之间做笛卡尔乘积，从而得到一系列参数组合。通过上一步骤，共得到3×3×1=9个参数组合，即：

第一个组合：P1=120，P2=184，P3=15；第二个组合：P1=120，P2=164，P3=15；

第三个组合：P1=120，P2=170，P3=15；

…

第九个组合：P1=100，P2=170，P3=15；

③求每一个参数组合出现的概率。比如，在上一步骤中，第一个组合出现的概率为P=P（P1=120）×P（P2=184）×P（P3=15）。

④筛选出出现概率最高的前M个组合。

（3）用Markov模型做最后的概率估算

基于Markov模型的推荐规格，如图3所示。

图3 基于Markov模型的推荐规格Fig.3 Recommended Specifications Based on Markov

①利用N-1阶Markov模型对每一个组合估算其条件概率。这里以二元模型为例，验证上文中组合出现的概率。第一个组合出现的条件概率为：

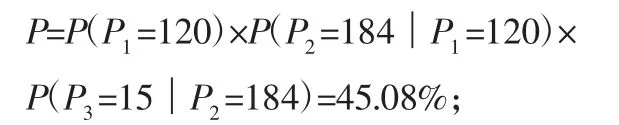
第二个组合出现的条件概率：

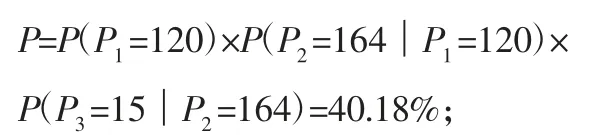
第三个组合出现的条件概率：

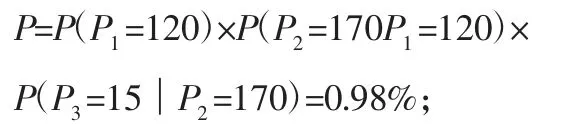
②将条件概率大于阈值的作为标准规格推荐给用户。Threshold是指阈值，阈值可以根据用户实际要求进行设定，如图4所示。这里的阈值设置为40%，若大于40%，系统则会推荐，反之不推荐。此外，这里N是指出现概率最高的前N个参数。从图3可知，基于Markov模型的推荐规格，系统依据阈值将两种规格推荐给用户。通过将设计数据中隐含的参数组合推荐给用户，用户根据自己的实际情况选择相应的规格，丰富用户的可选择性，降低出错率。

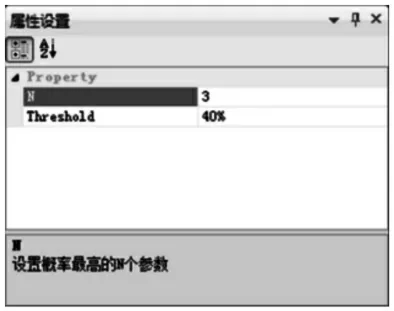
图4 推荐系统的阈值设定Fig.4 Recommended System Threshold Setting

5 结语

通过对Markov模型相关理论知识和应用进行研究与探讨，创新性的将Markov模型引入企业零部件标准规格推荐中，并基于C#编程语言，对NX软件进行二次开发。通过发掘参数化零部件参数组合的内在关系，得到先前并不含有的参数组合关系，有效得提高企业的零部件规格选择性。为提高产品设计效率、缩短产品开发周期、丰富产品种类和促进产品升级起到积极的作用。