滚动球式医疗服务型机器人动力学建模与仿真

刘 怡，钟文敏

（赣南医学院第一附属医院，江西 赣州 341000）

1 引言

由于新技术的推动和应用市场的拉动，近年来机器人在医疗方面的应用越来越广泛了，很多医院利用机器人分担一些例如消毒、输液、运输等服务型的工作。滚动球式机器人作为机器人的一种，因其运动灵活、通过性好等优点，在医疗领域有巨大的发展潜力[1]。

滚动球式机器人是在独轮自平衡机器人的研究基础上发展起来的，国内对滚动球式器人的研究起步较晚，目前大部分还处于理论研究阶段，国外在研究滚动球式机器人方面比较早的是文献[3-8]于2005年前后研制出一种新型的滚动球式机器人“Ballbot”，但是最成功的应该算是2010年，由苏黎世瑞士联邦理工学院与苏黎世应用科学学院以及苏黎世艺术学院合作研制的“Rezero”机器人[10-12]，“Rezero”机器人不仅能在球体上实现动平衡，而且具有非常强的灵活性和运动性，但是“Rezero”机器人在结构上缺乏失电保护装置，在机器人启停及瞬时失电的状态下整个机器人很容易倾倒，而且“Rezero”机器人动力学建模复杂且准确性不足，因此为了提高滚动球式机器人动力学模型的准确性及滚动球式机器人的安全性和稳定性，设计一种自带失电保护装置且建模简单、方便的滚动球式机器人就变得非常有必要了。

利用Solidworks设计出了一种新型的滚动球式医疗服务型机器人，该机器人通过增加失电保护装置有效的提高了机器人在启停及制动状态下系统的稳定性。同时，由于Lagrange-Routh方程同时具备了第一类和第二类Lagrange方程的功能[2]，通过引入了Lagrange乘子，使Lagrange-Routh方程建立的动力学系统模型理想假设更少、模型误差更小、求解过程更加简单，且能很好的解决滚动球式机器人系统的非线性、非完整性等问题，因此文中采用Lagrange-Routh方程对滚动球式机器人系统进行动力学建模。

2 滚动球式移动机器人结构设计

滚动球式机器人主要由机架、驱动机构、失电保护机构、球体四部分组成，如图1所示。其中机架上安装有各类型的传感器、三维惯性测量单元、锂电池、控制器、伺服驱动器等；驱动电机采用直流无刷伺服电机，三个全向轮对称安装在球体上，全向轮轴线与垂直方向成30°，全向轮中心、球体中心以及它们的接触点共线；失电保护装置主要由精密弹簧合页、圆形电磁吸盘、支撑板等组成，当通电运行状态下电磁吸盘紧吸支撑板，当系统瞬时断电或启停瞬时状态时电磁吸盘失电，四个支撑在弹簧的作用下同时打向地面防止整个机器人倾倒。由于驱动机构、失电保护机构、锂电池、控制器等都是固接在机架上，为了简化模型的计算，因此在建立模型前把固接在机架上的物体和机架当做一个整体称为主架体，由此，整个滚动球式机器人就可以看成是由主架体和球体两部分组成。

图1 滚动球式机器人本体结构Fig.1 Body Structure of Rolling Ball Robot

3 滚动球式机器人动力学建模

3.1 模型的理想化假设与参数设置

根据前面所设计的单新型球轮移动机器人本体机构建立相应的坐标关系，如图2所示。图2中坐标系OXYZ是全局固定惯性坐标系、坐标系O1X1Y1Z1是球体的动坐标系、坐标系O2X2Y2Z2主架体的动态坐标系，其中O是全局固定惯性坐标系的原点、O1是球体的球心也是球体动坐标系的原点、O2是主架体的质心点也是主架体动坐标系的原点。滚动球式机器人在全局固定惯性坐标系OXYZ中的姿态位置用固定在机架上的坐标系O2X2Y2Z2的位置来表示。为了表示坐标系OXYZ和坐标系O2X2Y2Z2之间的位置关系，引入欧拉角θ、φ、ψ及坐标系，如图3所示。同时假设，主架体的质心点O2（主架体动坐标系的原点）在全局固定惯性坐标系中的坐标为（x，y，z），球体的质心O1（球心）在全局惯性坐标系中的坐标为（x0，y0，z0）。

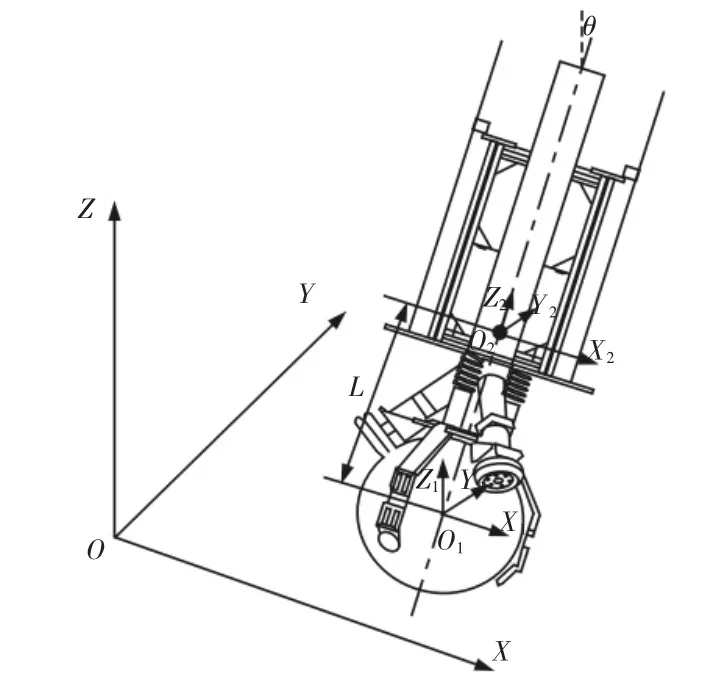
图2 滚动球式机器人坐标关系Fig.2 Coordinate Relation of Rolling Ball Robot

为了降低计算的复杂程度对模型做几点假设：（1）假设球体质心（球体圆心）与主架体的质心共线，且开始时滚动球式机器人处于平衡状态位于全局固定惯性坐标系的原点O，当受到瞬时的扰动运动到图2的位置；（2）假设球体与地面作纯滚动；（3）假设全向轮与球体之间的运动为纯滚运动。

图3 坐标系的旋转关系Fig.3 Rotation Relation of Coordinate System

3.2 广义坐标的设定

由于滚动球式机器人系统是非完整系统，在建模的过程中把该系统分为主架体和球体两部分。假设滚动球式机器人从全局固定惯性坐标系的原点运动到图2所示的位置球体绕X轴转过的角度为α，绕Y轴转过的角度为β，绕Z轴转过的角度为γ转动顺序X-Y-Z，而主架体质心在局部固定惯性坐标系中的坐标为（x，y，z），其姿态角可以用θ、φ、ψ来表示，假设球体的质心（球心）与主架体的质心共线，可以得到整个滚动球式机器人系统在全局固定惯性坐标系中的位置可以由参数x0，y0，z0，α，β，γ，x，y，z，θ、φ、ψ来表示，其中z0=R，R为球体的半径，由此，对整个系统分析，将整个系统分为球体和主架体两个部分，并分别对这两个部分进行建模分析，假设主架体的广义坐标为qz，则有qz=（x，y，z，θ，φ，ψ），球体的广义坐标的为qq，则有qq=（x0，y0，α，β，γ）。

3.3 球体动力学建模

Lagrange-Routh方程动力学建模的一般形式为[13-15]：

式中：qj—系统的广义坐标；Qj—广义坐标所对应的广义力；n—广义坐标的个数，其中n=9，L=T-V；T—系统动能；V—系统的势能；A—一个代表了k个Pfaff形式的非完整约束的k×n维的雅克比矩阵，且有A（q）q˙=0[1]。

首先对球体分析假设其广义坐标为qqj、P点的速度为VP、雅克比矩阵为Aq（qqj）、广义坐标对应的广义力为Qqj，动能为Tq，势能为Vq，则qqj可以表示为qqj=（x0，y0，α，β，γ），假设球体在全局固定惯性坐标系中的角速度为，根据文献[1、6、8]所述，则可表示为如下公式：

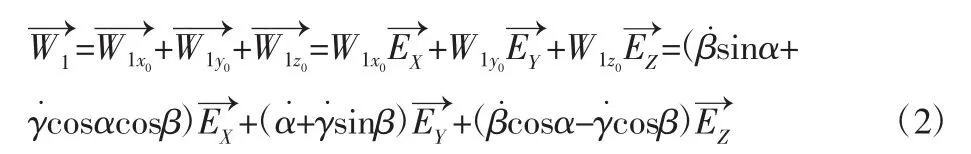
由于球体在地面上作纯滚运动，所以球体与地面的接触点瞬时速度为零，假设球体与地面的接触点为P，球体的半径是R，则有VP=0，且[9]：

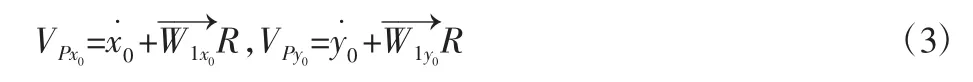
将式（2）代入到式（3）中可得：

对于新型滚动球式动机器人球体分析可知k=2，n=5，所以有：

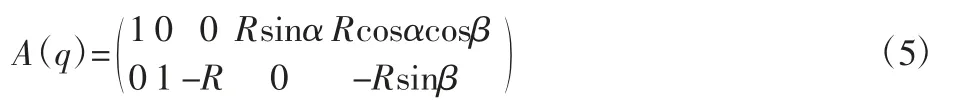
球体的动能、势能分别为Tq、Vq：

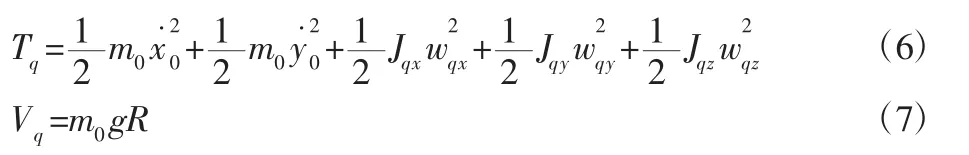
将广义力及球体的动能及势能带入到拉格朗日劳斯方程中得出了球体的完整动力学方程，具体形式如下：

再将式（4）代入（8）消去拉格朗日乘子λ1和λ2，得出球体的完整动力学方程，式（8）中Qq3、Qq4、Qq5分别为球体广义坐标α、β、γ所对应的广义力，根据球体完整动力学方程可知只要给出球体的运动状态及三个全向轮的输出扭矩便可求出球体广义坐标qqj＝（x0，y0，α，β，γ）的值。

3.4 主架体动力学建模

由于主架体不存在非完整约束，因此采用主动力部分为有势力的拉格朗日法对其系统进行动力学建模，假设主架体的角速度为w，总质量为m，Jzx、Jzy、Jzz分别表示主架体绕x、y、z轴的转动惯量，系统的动能为Tz，势能为Vz，则有：

结合拉格朗日方程可得主架体的完整动力学方程如下：

式中：q—主架体的广义坐标为qzj=（x，y，z，φ，θ，ψ），Qzj—主架体广义坐标所对应的广义力，矩阵M、C、G分别表示广义坐标的二阶导、一阶导、广义坐标的系数矩阵，矩阵中的元素的值可以根据拉格朗日方程解出。

4 滚动球式机器人动力学仿真与分析

为了验证滚动球式机器人动力学方程建立的是否准确运用MATLAB/SIMULINK软件对滚动球式机器人的动力学方程进行仿真分析。对于滚动球式机器人的运动主要分为三种情况，分别是原点自转运动、沿平面直线运动、沿平面曲线运动。根据这三种运动情况对所研究的滚动球式机器人进行仿真分析。仿真分析的相关参数的设定如下：m=15kg，m0=4.056kg，R=0.15m。

（1）当滚动球式机器人绕原点自转运动时，SIMULINK仿真结果，如图4所示。对于球体有x0=y0=α=β=0，对于主架体有x=y=θ=φ＝0，x=y=θ=φ＝0，z=L+R而球体的γ角和主架体的ψ角应该由零开始逐渐增大，大小相等，方向相反。根据图4可知球体和主架体的运动都符合实际运动规律。

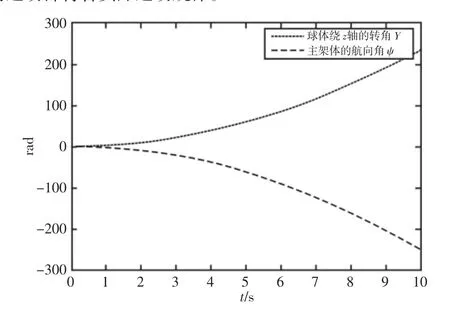
图4 滚动球式机器人绕原点自转运动时仿真结果Fig.4 Simulation Results of Rolling Ball Robot with Rotation Around the Original Point

（2）当滚动球式机器人沿y轴正方向直线运动时，MATLAB/SIMULINK仿真结果，如图5所示。对于球体有x0=β=γ=0，对于主架体有x=ψ=0，z=L+R，根据图5可知主架体的仰俯角和倾斜角在运动开始时出现突然增大后慢慢趋于零，主架体沿y轴运动的距离起始出现小范围的偏离原点后逐渐增大，对于球体其绕x轴的转角及沿y轴运动的距离都是逐渐增大，实际滚动球式机器人在刚开始运动时会出现短时的抖动，但很快将趋于稳定，仿真结果与机器人实际运动基本相符。

图5 滚动球式机器人沿y轴正方向运动时仿真结果Fig.5 Simulation Results of Rolling Ball Robot Moving Along the Direction of Y Axis

（3）当滚动球式机器人沿曲线运动时，假设沿y=x2（x＞0）运动，对于主架体有z=L+R，其MATLAB/SIMULINK仿真结果，如图6所示。实际中滚动球式机器人主架体的仰俯角和倾斜角起始有微小波动后逐渐趋于零，主架的航向角与球体绕z轴转动的角大小基本相等，方向相反且逐渐增大，球体绕x和y轴转动的角都是逐渐的增大，对于球体和主架体运动距离在x和y轴上的投影都基本相等且成逐渐增大的趋势，从图6的仿真结果图可知球体和主架体的运动基本符合实际的运动趋势。

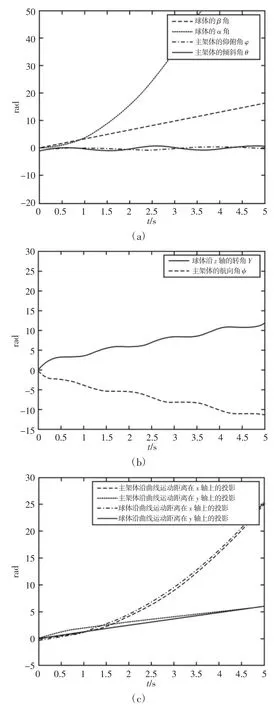
图6 滚动球式机器人沿曲线运动时仿真结果Fig.6 Simulation Results of Rolling Ball Robot Along the Curve

5 结论

（1）通过对已有的“Rezero”机器人进行系统的分析，设计出了一种滚动球式医疗服务型机器人，该机器人通过优化制动装置和增加失电保护装置，有效的提高了机器人的安全性和稳定性。（2）运用拉格朗日-劳斯方程对滚动球式医疗服务型机器人动力学建模，通过引入拉格朗日乘子，减少了方程的求解难度，弥补了拉格朗日方程无法计算约束反力的缺点，解决了该机器人系统的非完整性问题。（3）通过运用MATLAB/SIMULINK软件对建立的数学模型进行了仿真，验证了所建立的动力学模型的准确性，同时也为后续的结构优化和控制系统的设计提供了有力依据，具有较大的实际意义。