一种新型垂直轴风力机的气动性能分析

宋 磊，马 超，张明柱

（1.河南科技大学机电工程学院，河南 洛阳 471003；2.机械装备先进制造河南省协同创新中心，河南 洛阳 471003）

1 引言

随着全球化石能源的持续消耗，环境污染等问题日益突出。风能等清洁可再生能源已成为世界各国研究的一个重要方向。目前风能利用的主要形式是风力发电，风力发电机的两种主要类型是水平轴风力发电机（HAWTs）和垂直轴风力发电机（VAWTs）。水平轴风力机在大型风电场中得到大规模的发展和应用，已趋于饱和状态。垂直轴风力机逐渐受到人们的关注，而传统Savonius型垂直轴风力机的风能利用率低于其他类型风力机，但Savonius风力机具有结构简单，易于启动，无需调节风向，造价低廉且有利于低风速区的风能捕获等优点。

众多研究者在Savonius型风力机实验研究中取得了很多创新性进展。Mariano等人提出了增强Savonius风力机气动性能的两种方法：一方面是对风力机结构的创新改进，另一方面是建立一种对风向控制的系统[1]。而针对风力机结构的改进有三种方式，第一种针对叶片结构进行创新，文献[2]基于Savonius风力结构基础上，模仿莲花设计了一种微型风力机。第二种是增加辅助结构，如一些学者研究不同形状尺寸的端板和外部导流板等因素对风力机性能的影响[3]。第三种是通过多个风力机搭配组合提高风能转换效率，文献[4]研究Savonius型风力机在集群的性能，发现集群中各风力机的相互作用能够提升单体风力机的风能转换效率。对于风向控制方面，文献[5]提到了控制风向的三种方法，旨在提高S风力机性能。以上文献帮助更好认知到风力机结构的变化对气动性能的积极影响。许多研究者通过数值模拟对风力机进行分析与研究，如文献[6]结合k-ωSST模型进行S型风力机的非定常数值模拟，文献[7-8]采用计算流体动力学（CFD）数值仿真分析了S型风力机瞬态力矩。文献[9]采用计算流体力学软件Fluent分析了水平轴和垂直轴风力机的气动性能。参考以上文献，CFD数值模拟方法是研究垂直轴风力机气动性能的一种经济有效的手段。而文献[10]通过对比风力机之间叶尖速比对应的最大效率系数、最大扭矩系数，能够更全面了解改进后的Savonius型风力机的性能。所以该研究也采用无量纲叶尖速度比、扭矩系数和效率系数等参数对风力机性能进行探索和研究。

综上所述，提出了一种新型垂直轴风力机。由于它的叶片结构仿生鱼脊背曲线结构，所以将这种新型垂直轴风力机称为“鱼脊线翼型风力机”。构建了鱼脊线风轮结构并对其进行优化，利用滑移网格法与K-ωSST湍流模型对鱼脊线风力机气动性能进行了瞬态仿真预测。通过鱼脊线风轮与传统Savonius风轮结构气动性能对比，分析两种风力机内部风速流场变化对气动性能的影响。

2 建立模型

2.1 鱼脊线叶片模型

鱼类经历了一个漫长演化的自然过程，具备了出色的水中游动能力。流线形鱼体给设计者们提供了很多启发，如第一架超音速飞机起初就是模仿了剑鱼尖长且硬的上颌，还有模仿飞鱼滑翔的飞鱼导弹。许多研究团队会采用鱼体外形或鱼体运动的仿生，实现其结构优化及性能的提升。

从流体力学原理可知鱼体外形对游动性能影响很大。当鱼在水中运动时，它必然是由动量变化引起的，称为附加质量效应，以惯性力形式体现。当鱼横向摆动时，每一次在水中游动，造成额外的质量，局部惯性力即推力。而风轮叶片利用风的反作用力，将气流转化为旋转驱动的旋转力。借鉴水中游动的鱼体结构，将利用水动能的鱼脊背曲线应用到捕捉风能的叶片结构设计中，构建鱼脊线翼型叶片。

叶片翼型仿生鲫鱼的脊背曲线，保留其近似S型的几何特征，然后对曲线进行离散处理，提取其坐标点并生成数据文件。通过CAD软件将数据文件转化为初始鱼脊线叶片。

利用Matlab软件对鱼类游动模型的公式进行拟合，其关系式为：

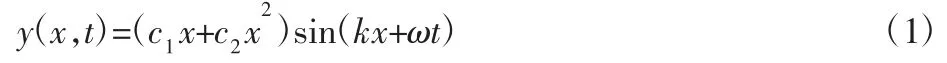
式中：y（x，t）—鱼体中心线的横向位移；

x—鱼体体长方向的位置坐标；

c1x+c2x2—振幅包络函数；

k—鱼体波动的数量；

鱼体波频率ω，ω=2πf，f—仿生鱼体的振荡频率。

以鱼脊背曲线为样本进行曲线拟合，建立笛卡尔坐标｛x，y｝，如图1所示。鱼头顶点为原点，x轴是鱼游动的方向，y轴是鱼脊背高的方向。初始的鱼脊线叶片曲线拟合关系式为：

基于仿生鱼脊叶片初始结构，对其进行了结构优化，利用圆弧的特点改善叶片结构，单叶片简化为两大、小圆弧反向拼接而成。为优化鱼脊线叶片，建立三因素、三水平的正交表，指标项目为叶片弦长L、小圆弧角度α和大圆弧角度β，如表1所示。

图1 初始仿生叶片的拟合曲线Fig.1 Fitting Curve of Initial Bionic Blade

表1 所选因素和水平Tab.1 Selected Factors and Levels

二维仿真对比后得出优化后鱼脊线叶片参数小圆弧角度α=26°，大圆弧角度β=91°，弦长L为354mm。小圆弧半径R1=193.5mm，大圆弧半径R2=191.5mm。

2.2 风轮结构模型

为鱼脊线风轮与传统Savnious风轮的二维模型，如图2所示。为了保持相同的扫风面积和雷诺兹数，建立模型的直径D均为700mm，高与直径比值为1：1，内腔直径S为100mm，叶片厚度为2mm和中心轴直径d为45mm。鱼脊线风轮是由均匀分布的三个叶片组成，叶片弦长L是354mm。而Savonius风轮是两叶片结构，其叶片弦长L为402mm。

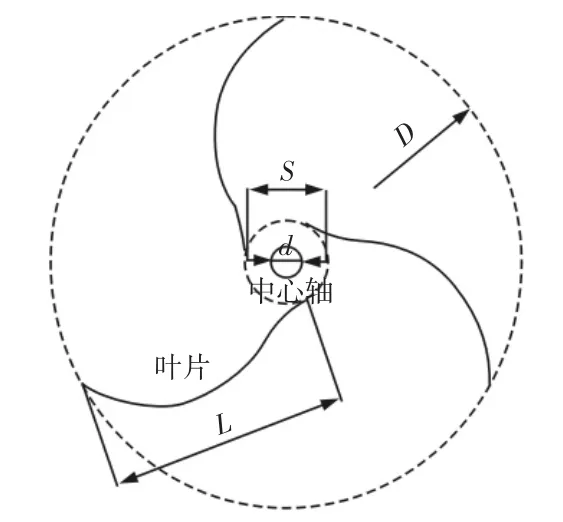
图2 风轮和叶片几何结构参数Fig.2 Geometric Parameters of Wind Rotor and Blade

3 数值模拟

3.1 湍流模型

由于垂直轴风力机在高度方向上不同位置的横截面相同，一般采用二维数值模拟研究风力机性能。k-ωSST模型具有较好的稳定性和收敛能力，能揭示更多的流动细节，并能准确地保证剪切应力的输送。涡流粘性μT和湍动能k及比耗散率ω的关系表示为：

k-ωSST模型是应用广泛的涡粘性模型，湍动能k以及比耗散率ω的运输方程表示为：

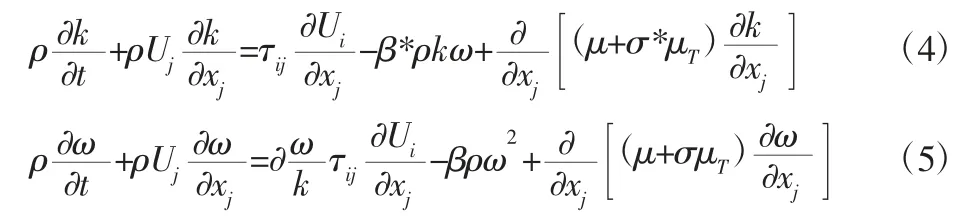
3.2 建立计算模型

采用ICEM CFD软件进行流场的网格划分。风力机中心到入口的距离是2100mm。在风轮中心处构建一个直径为900mm的圆形旋转区域。为了更准确地模拟风轮在流场中的实际工作状态，建立了一个巨大矩形风场，长度为14000mm，宽度3500mm。

为整个计算域和非结构三角形网格的示意图，如图3所示。计算域网格总数约为40万，内部旋转区域的网格数量为27万左右。圆形旋转区域的网格进行加密处理，特别是叶片和中心轴的边界层网格为多层矩形网格（prismatic layer）需要精确地设置。利用粘性网格间距计算软件求解出边界层第一层厚度为0.0317mm，设置20层，更准确的模拟叶片旋转。

图3 计算域的示意图与网格Fig.3 Schematic Representation and Mesh of the Simulation Domain

运用Fluent软件进行数值求解，来流风速为10m/s，方向自左向右，边界条件设置如下。（1）进口边界定义为速度入口（Inlet Velocity）；（2）出口边界为自由流出（Outflow）；（3）圆形旋转边界为滑移交界面（Interface）；（4）叶片设置旋转墙（movingwall）；（5）旋转轴设置壁边界（wall）；（6）两侧壁面边界为对称边界（symmetry）。

4 数值模拟结果与分析

效率系数Cp是指风力机旋转主轴的机械能与迎风面所受风能之比，是风力机性能的重要指标。风力机的效率系数越大，风能利用率越高。其计算公式为：

式中：T—模拟风轮的扭矩值（Nm）；n—转速（r/min）；ρ空气密度1.225kg/m3（当温度为15℃）；A—风轮扫风面积（m2）。

叶尖速比（TSR）是描述风力机性能的一个重要参数，是叶片尖端线速度与来流风速的比值。其计算式为：

式中：D—风轮直径（mm）；v—来流风速（m/s）。

为三种相同尺寸，不同叶片结构风轮的风能转换效率对比图，描述了三种不同风轮对应的风能转换效率系数Cp随着TSR变化曲线，如图4所示。结果表明，优化后鱼脊线风轮的最大转换效率比初始的鱼脊线风轮提升了12%。峰值效率达到23.57%。说明通过对鱼脊线叶片圆弧结构的优化改进有利于风能转换效率的提升。

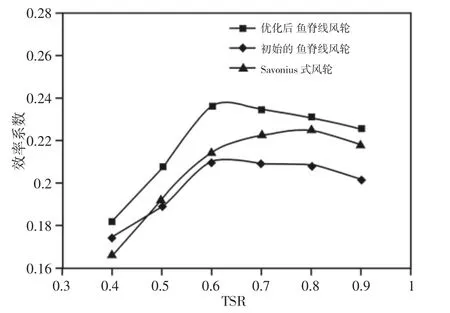
图4 叶尖速度比（TSR）与效率系数Cp的关系图Fig.4 Relationship Diagram Between TSR and Cp

从图4中可知，传统的Savnious式风力机的峰值效率为22.32%，低于优化后鱼脊线风轮的转换效率。通过对比最大风能转换效率与TSR之间的关系可以发现：在TSR为0.6时优化后的鱼脊线风轮达到峰值效率，Savnious式风轮的峰值效率出现在TSR为0.8时。在恒定风速下，由式（8）可以得知风轮旋转速度与TSR呈正比关系，优化后的鱼脊线风轮在较低TSR范围达到峰值效率，说明定风速下，它在相对低的转速情况下产生的效率高于Savnious式风轮。可以得出，优化后鱼脊线风轮在低风速地区的风能捕获中具备一定的优势。

为扭矩系数随叶尖速比的变化曲线，如图5所示。随着TSR的增加，三种风轮产生的扭矩系数均呈现递减的趋势。且优化后鱼脊线风轮的扭矩系数高于Savnious风轮和初始的鱼脊线风轮。这意味着，优化后鱼脊线叶片结构的气动性能优于传统的半圆形叶片结构，旋转过程中获得更高的转矩，获得更高的风能转换效率。

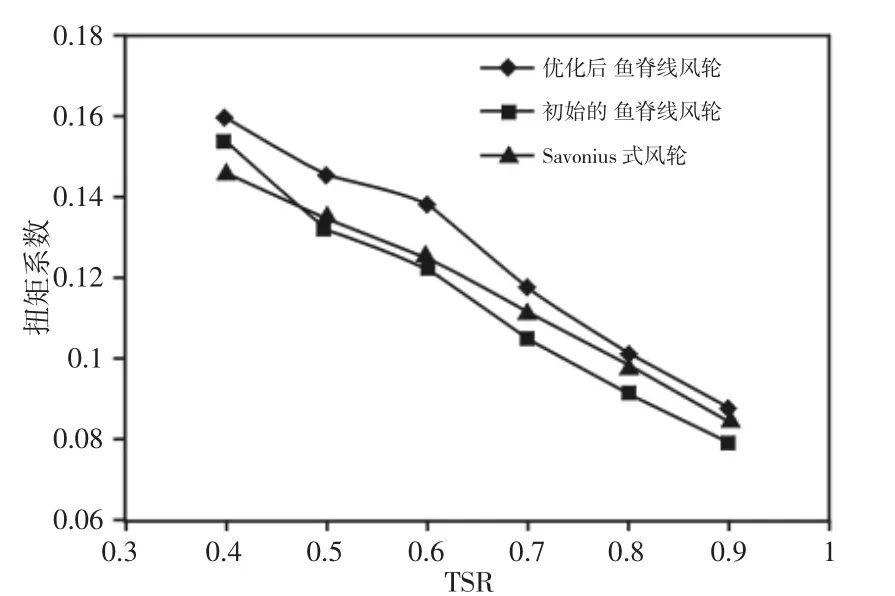
图5 叶尖速度比（TSR）与扭矩系数CM关系图Fig.5 Relationship Diagram Between TSR and CM

为两种风轮的不同方位角θ的风速矢量变化，如图6所示。对于Savnious风轮，采用的是两叶片结构，在内部重叠区域的气流会产生剧烈弯折，而剧烈弯折会造成涡流，涡流的形成导致了能量损耗，从而降低了风能的转换。而鱼脊线风轮采用的三叶片均布结构，内部有一个由中心轴与三叶片小圆弧形成的内腔，可以起到引导气流的作用。当气流沿叶片末端穿过内腔，会冲击到前一叶片的凹处产生第二次驱动力，从而实现风能转换效率提高。从图6可知，Savnious风轮在方位角θ为30°和60°的位置，有一个逆时针旋转的涡流出现在推进叶片凹面。它对气流有负面影响，干扰气流对叶片的冲击，随着推进叶片进入迎风侧，在方位角θ为120°涡流逐渐消失。同时，观察到图6的鱼脊线风轮在方位角30°和60°时，有一个逆时针旋转涡流在推进叶片的凸面产生。这个位置的涡流会影响前一叶片凹面的风能吸收。随着方位角的变化，涡流位置也在改变，涡流的产生会影响风轮对风能的利用。通过两种结构风轮的对比，可以看出它们的风速矢量之间存在一定差异。分析其主要影响因素是叶片结构，如圆弧角度，它不仅影响着气流对前进叶片凹面的冲击方向、还关系到涡流的产生。

图6 不同旋转角对应的风速矢量变化Fig.6 Velocity Vectors Versus Angular Position

5 结论

本研究采用二维瞬态数值模拟方法研究风轮的气动特性。构建了两种风轮结构计算模型，对鱼脊线风轮与传统Savnious风轮进行仿真对比分析。得到以下结论：（1）优化后鱼脊线风轮的扭矩系数和效率系数均优于传统Savonius风轮，且在较低叶尖速比（TSR=0.6）达到峰值效率23.57%，并且优化后的鱼脊线风轮比初始鱼脊线风轮的风能转换效率提升了12%。（2）通过风场的速度矢量图分析鱼脊线风轮结构的气动性能。发现由三个小圆弧和中心轴围成的鱼脊线风轮内腔，能起到转折气流的作用。当气流沿叶片末端流动，穿过内腔，冲击叶片凹处产生第二次驱动力，从而提高风能转换效率。发现叶片圆弧曲率对风轮效率会产生很大影响。在接下来的研究工作中，将鱼脊线叶片与鱼游动模型相结合重构风轮结构。探讨不同曲率变化对风力机性能的影响，以期得到一种更高风能转换效率的风力机。