不等深梯形槽干气密封的研究及槽型优化

邱海涛，陈志，范唯超，吉华，李建明

不等深梯形槽干气密封的研究及槽型优化

邱海涛，陈志*，范唯超，吉华，李建明

（四川大学 化学工程学院，四川 成都 610065）

针对相同的平面结构，设计出多种不等深梯形槽结构，建立了相关干气密封端面流场的数值计算模型。利用Fluent软件对流场进行数值模拟，获得了不同膜厚下不同结构的气膜刚度、开启力、泄漏率、刚漏比等数据，研究结果表明不等深阶梯槽的刚度、刚漏比比平底槽高，但开启力比平底槽低些。使用正交优化计算进一步探究槽深、槽数、入口角、槽宽比、槽长坝长比对开启力、泄漏率对发散阶梯梯形槽密封性能参数的影响。该工况下，发散型梯形槽最优设计方案为：最大槽深为10 μm、槽数为12、入口角为12°、槽宽比为0.88、槽长坝长比为0.78，研究结果为相关密封设计研究提供了一定的参考。

干气密封；梯形槽；不等深槽；正交优化计算

干气密封（Dry gas seal，DGS）起源于20世纪60年代末，由气体润滑轴承发展而来，干气密封能够形成微米级别的气体薄膜，实现“以气封气”，相比于传统的机械密封，干气密封具有磨损小、泄漏小、寿命长、能耗低、操作简单且可靠性高等诸多优点[1]。干气密封的气膜不稳定会导致干气密封的磨损[2]，干气密封槽型对于气膜刚度影响很大，因此在干气密封的研究发展中，关于槽型的研究一直是一个重点。20世纪末，John. Crane、EG&G SEALOL、NOK Eagle、Burgman等公司就研发了径向直线槽、中间环螺旋槽、直线槽、倒T形、V形槽和交叉圆弧槽、Y形槽、人字形槽等槽型[3-4]。国内的宋鹏云[5]、彭建[6]、杨惠霞[7]、彭旭东[8]、王玉明[9]等一大批技术专家开展端面开槽技术的研究和试验，研究和设计出T型槽、V型槽、人字型槽、树型槽、燕尾槽、“八”字型螺旋槽等新槽型的干气密封。随着计算机技术的发展，数值模拟被大规模的应用于干气密封的研究，丁雪兴[10-11]、张伟正[12]等应用PH线性化方法等求解雷诺方程，对螺旋槽干气密封进行优化设计，以期获得最佳几何参数。宗聪等[13]采用有限差分法求解二维稳态雷诺方程，数值分析了周向槽宽比、径向槽宽比和槽深比等结构参数对似叠罗汉槽干气密封性能的影响规律,获得了似叠罗汉槽主要结构参数的优选值范围。陈文奇等[14]利用数值方法分别研究槽数、螺旋角、槽深、气膜厚度、槽台比以及转速对密封性能的影响规律。上述研究通常通过数值模拟的方法考察单一因素对于密封性能的影响，胡琼等[15]对有序微造型的圆弧线槽干气密封性能进行分析，分析了各个参数对密封性能的影响，进一步探究了各参数的影响程度，陈志等[16]则从实际工况出发，考虑端面变形锥角对干气密封性能的影响。国内也有学者将等深的螺旋槽改进成不等深螺旋槽，使用MATLAB数值模拟方法对其密封性能进行研究，发现收敛型不等深槽比等深槽拥有更好的密封性能，泄漏量更小[17]。本文使用Fluent对流场进行三维数值模拟，并引用正交优化设计的方法以求得本次工况条件下的最佳密封结构。

双向旋转梯形槽干气密封具有泄漏率非常低的优点。本文在双向旋转梯形槽干气密封[18]的基础上，通过改进梯形槽干气密封的的结构获得更佳的气膜刚度，提升工作稳定性。本文提出了三维槽型的设计，并对密封性能进行比较，最后对发散型阶梯梯形槽密封的几何参数进行正交优化设计。

1 梯型槽内流场边值条件

1.1 基本假设

由流体力学基本理论，结合DGS工况特性做出如下假定：

（1）气膜虽然只有微米级，但相对于分子间隙仍然很大，仍然视气膜流体为连续介质；

（2）气体分子与端面无相对滑移；

（3）流体流动为层流；

（4）属于牛顿黏性流体，主要受黏性剪切力影响；

（5）流体域流体稳态层流流动

（6）气体黏度为常量，并且保持不变。

流体域中的流体流动的-方程为：

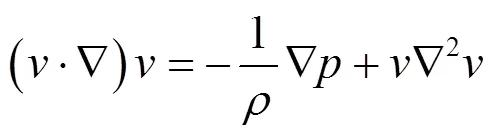
使用开启力、闭合力、气膜刚度、泄漏率和刚漏比等参数表征梯形槽干气密封的性能：

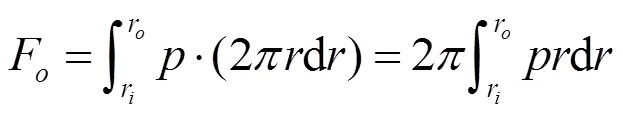
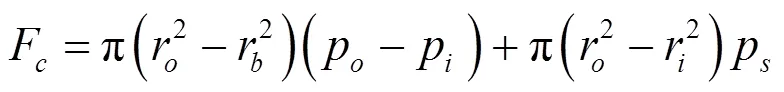
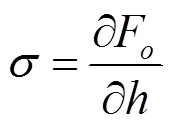
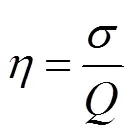
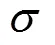
1.2 几何模型

梯形槽干气密封环的端面结构如图1所示，其最大的特点是在周向上分布着许多近似于梯形的浅槽组，每个槽组由根径（R）圆弧与两条对称斜线构成，圆弧与斜线之间圆弧过渡，形成近似等腰梯形槽。开槽区称为“动压槽”，两开槽区之间的平台区域称为“密封台”，槽根径与端面内径的平面区域称为“密封坝”，靠它的节流作用来限制泄漏量。

图1 梯形槽干气密封端面槽形及结构参数图

同时，对于端面结构做出如下定义：

（1）槽深：动压槽端面到槽底的深度；

（2）槽宽比：端面外圆周上槽的周长与整个圆周长之比，也等于端面外圆周上单个槽弧长与单个槽弧长加上密封台弧长之和之比。

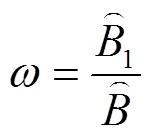
（3）槽长坝长比：槽的最大径向长度与密封端面的径向长度之比。

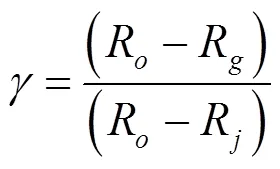
（4）入口角：槽斜线与该斜线在外圆周上交点处过圆心射线的夹角。

（5）槽数：密封环上周向均匀分布的梯形圆弧槽数目。

基于图2所示的等深梯形槽相同的横截面结构，设计出的4种不等深梯形槽的三维槽型，分别为收敛型阶梯不等深槽、发散型阶梯不等深槽、收敛型锥度不等深槽及发散型锥度不等深槽，其横截面结构如图3所示，泄漏方向如箭头所示，沿泄漏方向，槽深变小为收敛型槽，反之为发散性。阶梯槽均由5个等宽等高的阶梯实现外径到坝区的过渡，而斜度槽则是由一个等锥度的斜坡过渡。几何参数相同时，当阶梯级数无限增加时，阶梯槽与斜度槽二者锥度一致，均为：

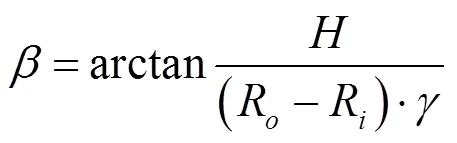
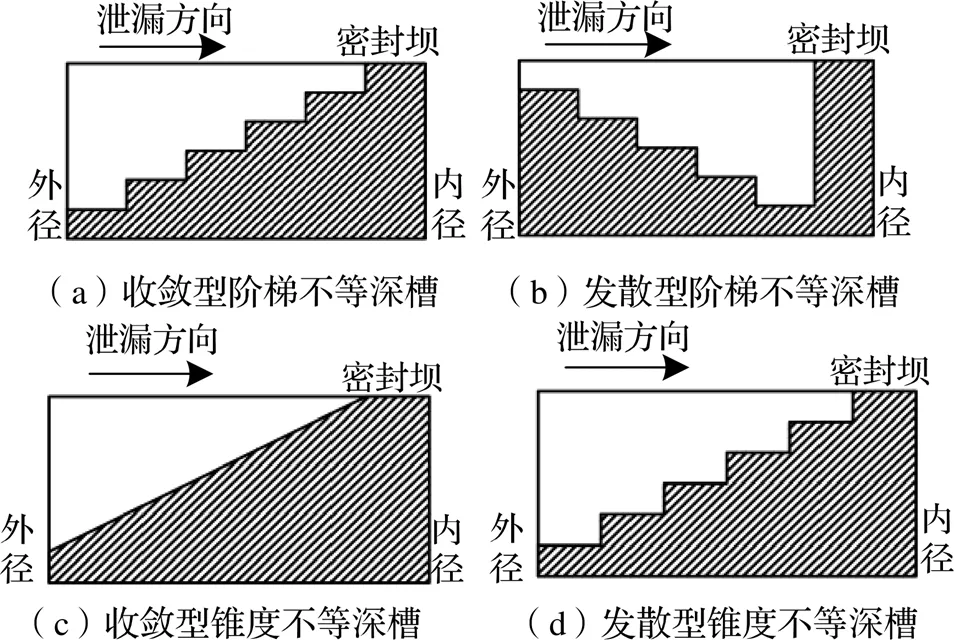
图3 不等深梯形槽截面图

1.3 边界条件

以密封端面之间的气膜为研究对象，其介质为2，工作温度为323 K，转速为985 r/min。由于梯形槽干气密封存在周期性且均匀分布的梯形槽，故可以选用密封端面的一个槽区加坝区的组合部分作为计算域，槽的入口与坝区的出口分别为压力进口与压力出口边界条件，进口压力为0.38 MPa，出口压力为0.1 MPa，两侧为周期性边界条件，如图4所示。

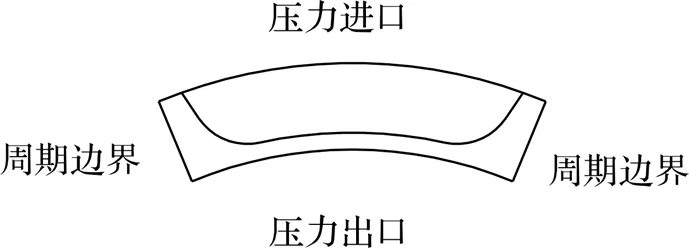
图4 计算域边界条件

1.4 网格划分

模型的轴向尺寸与径向尺寸跨度较大，属于跨尺度问题，给网格划分带来了一定的难度，以等深梯形槽为例，其外径R为138 mm，内径R为110mm，槽数为8，入口角为14°，槽长坝长比为0.68，槽宽比为0.88，模型坝区厚度2 μm。首先研究平底槽，其槽区厚度为8 μm，在前处理原件Gambit中建立模型并划分网格，划分网格时需要轴向放大1000倍，然后采用Pace-Cooper划分网格，将坝区分为4层、槽区分为16层，共114460个六面体网格。其次研究不等深槽，其最大深度仍然为8 μm。其余槽型的网格划分方法相同。

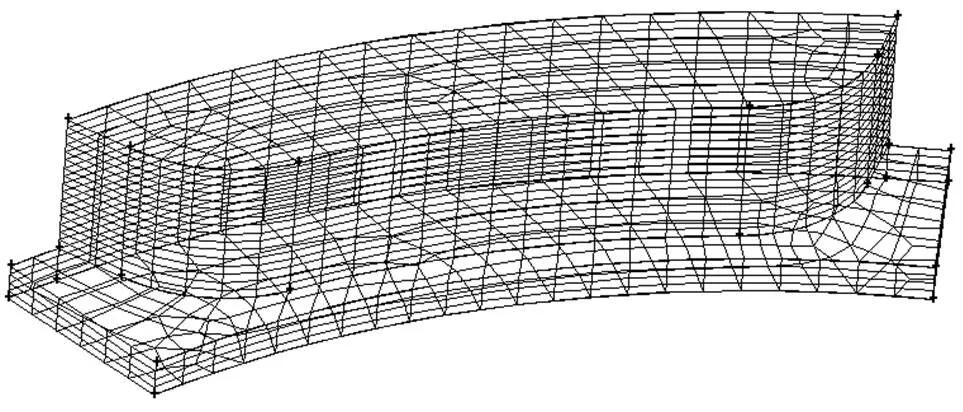
图5 等深梯形槽计算区域网格

1.5 求解方法

采用Fluent 3D分离的隐式求解器，压力差值选择标准差值，压力速度耦合采用SIMPLE算法，对流项、扩散项离散格式分别为二阶迎风格式和中心差分格式。

1.6 网格无关性验证

合理的网格数量对于计算速度有重要意义，以坝区厚度为2 μm，针对图5所示平底槽，以槽区厚度为8 μm的等深梯形槽模型为例，选取网格数量3.5～40万的网格数量进行计算考察网格数量对于开启力大小的影响，结果如图6所示，可以看出，网格数量达到114460时，所计算的开启力趋于稳定，可认为此时满足网格无关性。其余4种不等深槽的网格无关性验证相同。

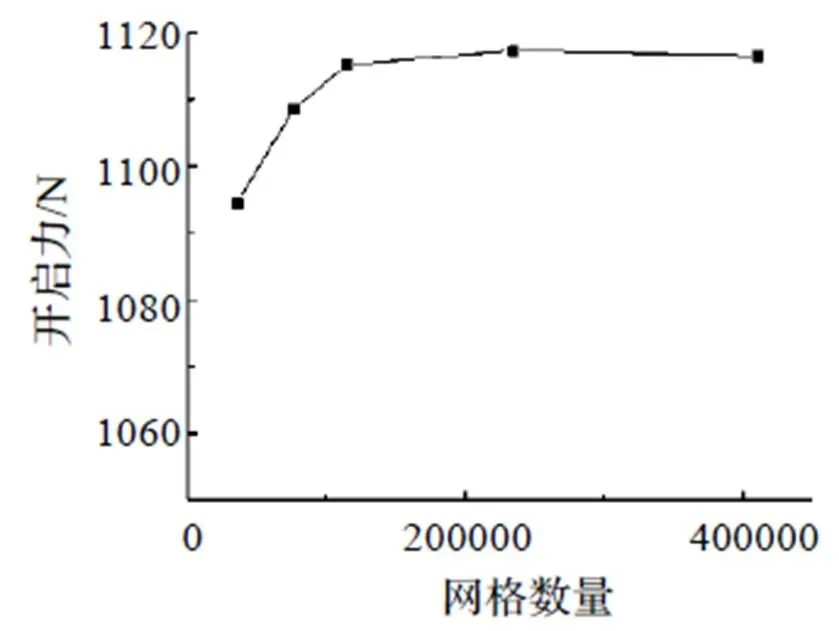
图6 等深梯形槽网格无关性验证

2 各槽型性能对比分析

在干气密封稳定运行时，使用SolidWworks建立各种槽形的微间隙气膜模型，导入Gambit中划分网格并定义边界条件，将网格导入Fluent中进行数值求解，当各个参数的残差值随计算步骤的增加而降低，而后曲线趋于平缓且进出口处流量满足质量守恒时，认为计算收敛并对五种槽形的开启力、泄漏率、气膜刚度、刚漏比等4个密封性能指标进行分析。计算结果如图7～图10所示。

从图7中可看出，相较于等深槽，各种不等深槽的气膜刚度受气膜厚度的影响较大，且具有相似规律。在气膜厚度为2～4.2 μm，不等深槽的气膜刚度均高于等深槽，发散型阶梯槽明显优于其他4种槽型，具有最佳的气膜刚度。

从图8中可以看出，两条收敛型不等深槽性能曲线几近重合，两条发散型不等深槽的性能曲线也几近重合，且在2～5 μm的膜厚范围内，发散型不等深槽具有最低的泄漏率，而且，随着膜厚的增加，发散型不等深槽具有最小的增量，在泄漏率这一项上，不等深槽的表现均要优于等深槽。

图7 气膜刚度随膜厚的变化图

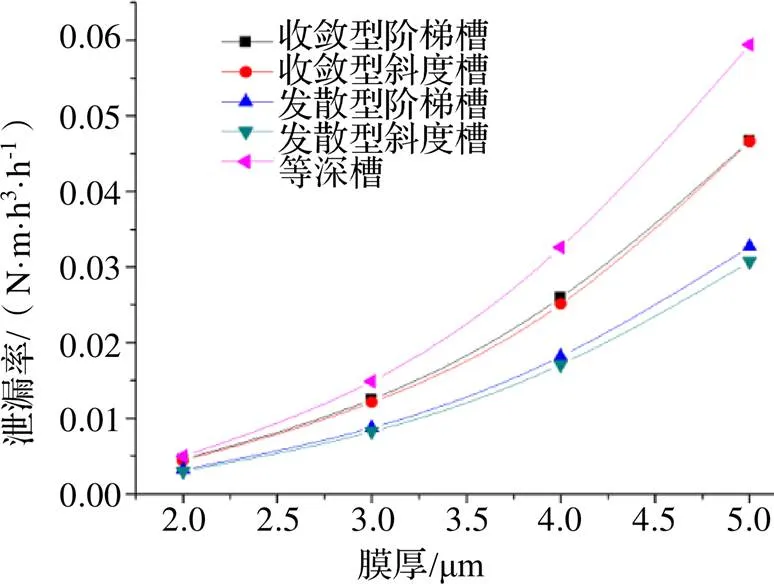
图8 泄漏率随膜厚的变化

从图9中可以看出，在刚漏比这一项上，收敛型槽的性能曲线几近重合，发散型槽的性能曲线也几近重合，发散型不等深槽具有最大的刚漏比，且在气膜厚度为2 μm时最为明显，不等深槽的刚漏比均大于等深槽。

从图10中可以看出，在开启力这一项上，收敛型槽的性能曲线几近重合，发散型槽的开启力性能曲线也几近重合，在2～5 μm的膜厚范围内，等深槽具有最大的开启力，发散型槽的开启力最低，这一点在干气密封的结构设计时需要考虑，虽然发散型槽的泄漏率、气膜刚度、刚漏比三个指标比较优秀，但存在开启力较低的问题，好在只要平衡直径设计好，工作时密封端面就能正常开启，不影响其正常运转。

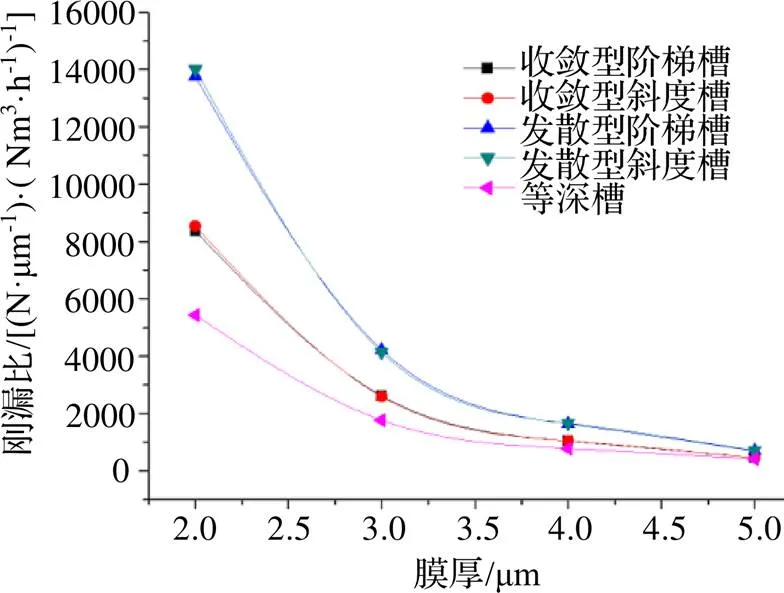
图9 刚漏比随膜厚的变化

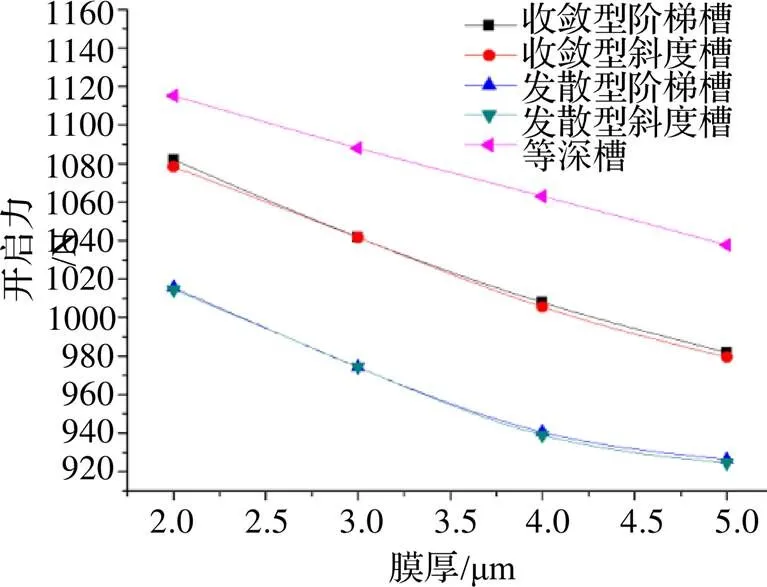
图10 开启力随膜厚变化

综合对比以上曲线图，可以看到，在气膜刚度、刚漏比、泄漏率这三个密封性能指标上发散型槽均优于收敛性槽、等深槽。分析其主要原因是：密封端面旋转时，端面之间的气体具有较高的动能，并被带入发散型梯形槽内，气体从槽入口流至密封坝，由于间隙在逐渐增大，因而气体流速降低，在槽底部密封坝处气体流速降至最低，从密封坝逃逸出去的气体减少，故泄漏量降低，与之相反，收敛型槽由于其间隙逐渐变小，气体从槽入口流至密封坝时，气体流速逐渐变大，从而从密封坝逃逸出去的气体相对发散型槽会较高；同时发散型动压效应较好，进一步表现出较好的刚漏比。对比发散型阶梯不等深槽和发散型锥度不等深槽，发现他们的性能有微弱差别，主要是阶梯效应的作用，由于目前干气密封槽的加工采用激光加工，阶梯槽加工更加方便（由于激光加工时，斜度槽是通过取较多级数的阶梯槽来实现的），本文研究的阶梯槽取了5阶梯，其各项性能与斜度槽近似程度已经很高。总体来讲发散型槽具有更为优越的密封性能，但是需要注意的是其开启力是小于平底槽的，好在这个问题可以通过调整密封平衡直径达到力的平衡。

3 梯形槽干气密封的优化设计

由于发散型阶梯梯形槽密封气膜刚度和刚漏比更佳，故继续对这种槽型的几何参数进行正交试验优化设计。

3.1 数值模拟试验方案

为了研究分析发散型阶梯梯形槽干气密封几何参数对其密封性能的影响，本文以最大槽深、槽数、入口角、槽宽比、槽长坝长比为5个因素，由于本文中模型内径与外径均为定值，由式（7）可知，阶梯槽与斜度槽的锥度由最大槽深与槽长坝长比的比值唯一确定，故不再对锥度单独讨论，以开启力F、泄漏率、气膜刚度、刚漏比为指标设计五因素四水平正交试验。水平因素表如表1所示，并选取正交试验表L16（45）。

3.2 极差分析

按照前述试验方案表和试验步骤，进行模拟试验，得到的各组实验结果数据汇于表2中，并采用极差分析法对试验结果数据进行分析。

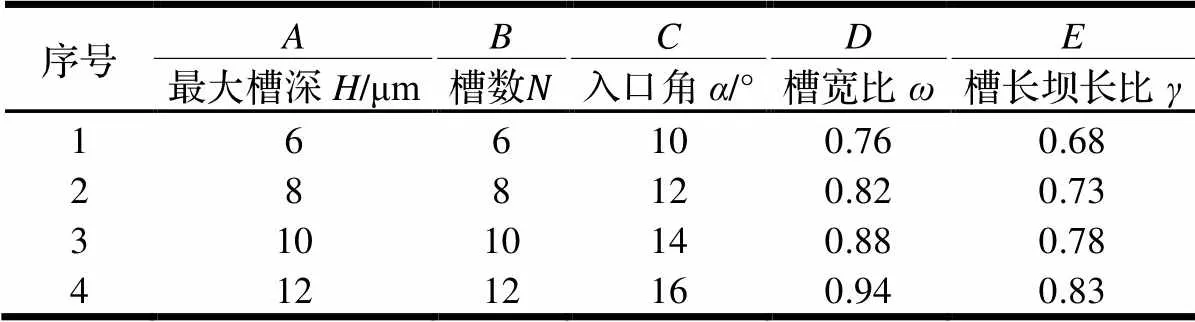
表1 几何结构参数正交模拟试验水平因素表

表2 各密封性能指标的正交试验数据记录

由于四个指标单独分析得到的优化条件并不一致，须得根据因素的影响主次顺序，综合考虑，去找出最佳的端面槽型几何参数组合。现采用综合平衡法对每个因素进行分析，综合考虑，最终确定最优端面几何参数组合。

对于因素，最优组合中多项因数均指向3，而从影响程度来看，槽深对于气膜刚度与开启力的影响均较大，综合考虑，槽深最优参数为3。

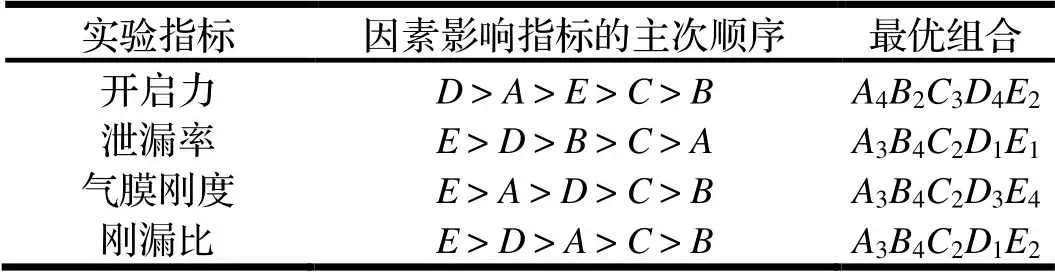
表3 各因素最优组合以及对各指标的影响大小

对于因素，其主要影响的实验指标为泄漏率，其最优组合指向4，而其他实验指标中也有多项最优组合指向4，综合考虑，槽数最优参数为4。

对于因素，其对实验指标的影响程度均处于第四位，多项最优组合指向2，因此，吸入角最优参数为2。

对于因素，其主要影响的实验指标为开启力，综合考虑其对泄漏率、气膜刚度、刚漏比的影响，槽宽比最优参数为3。

对于因素，其对泄漏率、气膜刚度、刚漏比的影响都很大，其最优组合指向也不同，综合考虑，选取各项实验指标表现较好的3。

经过综合平衡法的分析，得出本试验的优化组合方案为最大槽深10 μm、槽数12、入口角12°、槽宽比0.88、槽长坝长比0.78。

4 结论

（1）不等深槽的刚度在较低的气膜厚度下比等深槽高，而泄漏率比等深槽低，因此不等深槽有较好的优势。但开启力却是等深槽更大。

（2）在研究范围内，在气膜刚度、刚漏比、泄漏率这三个密封性能指标上发散型槽均优于收敛性槽。发散型阶梯不等深槽和发散型锥度不等深槽的密封性能有微弱差别，当台阶级数较高时，可以忽略其差别。

（3）在本工况下，由综合平衡法确定出发散型阶梯形梯形槽的最优组合为最大槽深为10 μm、槽数为12、入口角为12°、槽宽比为0.88、槽长坝长比为0.78。

[1]Wasser J R. Dry seal technology for rotating equipment[J]. Lubrication Engineering，1994，50（3）：247-252.

[2]左超. 离心压缩机干气密封损坏及原因分析[J]. 机械，2018，45（3）：78-80.

[3]Basu P. Analysis of a Radial Groove Gas Face Seal[J]. ASLE Transactions，1992，35（1）：11-20.

[4]LaiT. Development of non-contacting, non-leaking spiral groove liquid face seals[J]. Lubrication Engineering，1994，50（8）：625-631.

[5]宋鹏云. 旋槽上游泵送机械密封性能影响因素分析[J]. 润滑与密封，2000（3）：50-53.

[6]彭建，左孝桐，王福. 同槽型气体端面密封研究[J]. 流体机械，1996，24（11）：8-12.

[7]杨惠霞，顾永泉. 圆弧深槽热流体动压机械密封理论研究[J]. 流体机械，1997，25（9）：12-18.

[8]彭旭东，谭丽丽，盛颂恩，等. 带内环槽的螺旋槽干式气体端面密封的静压性能[J]. 摩擦学学报，2008，28（6）：507-511.

[9]王玉明，王强，吕岩，等. 高速透平压缩机用螺旋槽端面密封机系统的研制[J]. 流体工程，1992，20（4）：1-7.

[10]丁雪兴，蒲军军，韩明君，等. 基于二阶滑移边界的螺旋槽干气密封协调优化[J]. 中国石油大学学报（自然科学版），2012，36（3）：140-145.

[11]丁雪兴，陈德林，张伟政，等. 螺旋槽干气密封微尺度流动场的近似计算及其参数优化[J]. 应用力学学报，2007，24（3）：425-428.

[12]张伟政，俞树荣，丁雪兴，等. 螺旋槽干气密封系统轴向振动响应及结构优化[J]. 排灌机械工程学报，2010，28（3）：228-232.

[13]宗聪，彭旭东，江锦波，等. 似叠罗汉槽干气密封的结构优选与性能研究[J]. 摩擦学学报，2017（1）： 121-129.

[14]陈文奇，李志强，吴云柯，等. 双螺旋角槽干气密封的槽型优化设计[J]. 润滑与密封，2018（7）： 23-30.

[15]胡琼，王衍，戴嵘，等. 基于有序微造型的圆弧线槽干气密封性能分析[J]. 化工学报，2019，70（3）： 1006-1015.

[16]陈志，赵鹏，王金红，等. 端面变形锥角对干气密封性能影响的数值模拟[J]. 工程科学与技术，2018，50（1）：203-210.

[17]宋文博，李双喜. 不等深螺旋槽干气密封性能的研究[J]. 润滑与封，2010，35（4）：80-84

[18]陈志，范唯超，陶杰，等. 双向旋转梯形槽干气密封流场的数值模拟[J]. 四川大学学报（工程科学版），2015，47（1）：180-185.

Optimization of Unequal Depth Trapezoidal Grooves for Dry Gas Seals

QIU Haitao，CHEN Zhi，FAN Weichao，JI Hua，LI Jianming

( CollegeofChemicalEngineering, SichuanUniversity, Chengdu 610065, China)

A variety of trapezoidal groove structures with unequal depth are designed on the same plane structure, and the numerical calculation model of the flow field on the end face of the dry gas seal is established. The convection field is simulated with FLUENT software. Consequently, the stiffness, opening force, leakage rate, and stiffness leakage ratio of different structures under different film thickness are obtained. The research results show that the stiffness, stiffness leakage ratio of different depth stepped grooves are better than those of flat bottom groove, but the opening force is lower than that of flat bottom groove. The orthogonal optimization calculation is used to further explore the influences of groove depth, groove number, entrance angle, groove width ratio, groove length dam length ratio on the opening force, leakage rate and other sealing performance parameters of diverging ladder trapezoidal groove with unequal depth. Under this working condition, the optimal design scheme of divergent groove is: the maximum groove depth is 10 μm, the number of grooves is 12, the entrance angle is 12°, the groove width ratio is 0.88, and the groove length dam length ratio is 0.78.

dry gas seal；trapezoidal groove; unequal deep groove；orthogonal optimization calculation

TB42

A

10.3969/j.issn.1006-0316.2020.04.004

1006－0316 (2020) 04－0020－07

2019－10－28

邱海涛（1995－），男，湖南娄底人，硕士研究生，主要研究方向为流体密封技术。

陈志（1962－），女，四川成都人，教授，主要研究方向为流体密封技术和流体机械，chenzhi_hx@scu.edu.cn。