互通式立体交叉匝道纵断面接坡方法分析

2020-05-21

中国公路 2020年8期

（中交第二航务工程勘察设计院有限公司，湖北武汉 430060）

一、引言

互通式立交匝道与主线相接处，是指立交匝道与主线的分岔端，也称楔形端，如下图1PON所示。其中，匝道纵断面起点接坡问题是匝道设计中的一个重要部分。匝道端部纵坡是一个合成坡度，它与主线的纵坡值、路面横坡及匝道与主线的平面线形等有关。关于匝道端部纵坡的计算方法，设计者因各人选用的方法以及各方法取值的不同，计算出的结果往往不一致。下面笔者以江西上浦高速公路的信州互通为例，对互通式立体交叉匝道纵断面接坡方法进行探讨。

图1. 互通式立体交叉楔形端部图

二、技术思路

目前关于匝道起始纵坡的求解主要有四种方法：（1）从小鼻端往后取5m，首先从主线中心线C点的高程推算出A点的高程，然后通过，求出匝道起始纵坡；（2）从小鼻端往后取10米，首先从主线中心线D点的高程推算出B点的高程，然后通过，求出匝道起始纵坡；（3）采用主线纵坡的切线坡；（4）依据矢量合成原理，对主线纵坡考虑横坡和端部出入口角的修正，匝道起点纵坡可按下式进行计算：。

当主线与匝道的分、合流点处于直坡段时，匝道纵断面线形容易与主线保持一致，当分、合流点位于主线竖曲线范围内时，如果忽略匝道竖曲线的影响去设计匝道纵坡时，这时就会造成分、合流点附近匝道路面与主线路面形成一段路拱，容易造成积水且不利于行车的安全性。鉴于此，笔者从分、合流点位于主线直坡段和竖曲线段分别对上述四种方法进行对比分析。

三、技术方法

（一）分、合流点位于主线直坡段

信州互通D匝道起点小鼻端N点（匝道纵断面设计起点）位于主线直坡段，对应主线纵坡i=-1.3%。设匝道计算纵坡的两个点之间的间距为L。首先取L=-5m进行匝道起点纵坡计算，同时选取L=-5m，L=-10m，L=-15m，取平均值得到的纵坡进行比较分析。

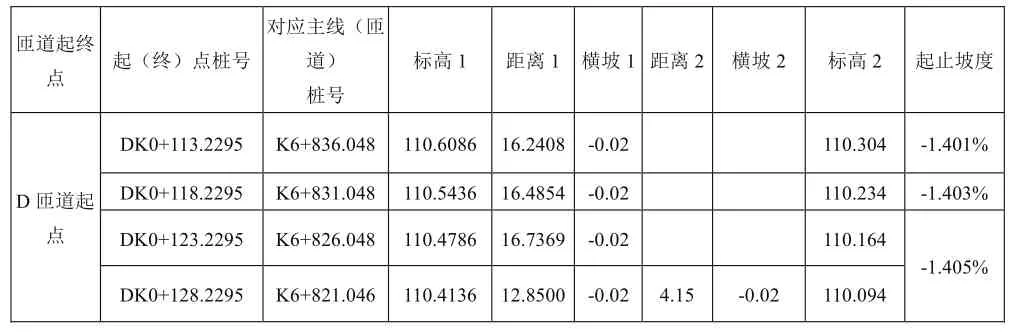
表1. 信州互通匝道接坡计算中间数据（L= -5m）

通过计算发现L=-5m时，匝道起点纵坡i=-1.405%，三次计算取平均值得到i=-1.403%。

选取L=-10m进行匝道起点纵坡计算，同时选取L=-10m，L=-20m，L=-30m，取平均值得到的纵坡进行比较分析。

表2.信州互通匝道接坡计算中间数据（L= -10m)

通过计算发现L=-10m时，匝道起点纵坡i=-1.403%；三次计算取平均值得到i=-1.410%。

第三种方法，采用主线纵坡的切线纵坡，由于主线在匝道端部附近为直坡段，故主线的切线纵坡即为主线纵坡，i匝=-1.3%。第四种方法根据i匝=i主×cosθ+i横×sinθ，首先求得主线P点和匝道N点的方位角之差为3°。

得到i=-1.3% × cos3o-0.02× s in 3o=-1.403%。

将上述纵坡与主线对应变速车道的中心线实际的高程放在一个坐标系中进行对比分析（L=-5m时，匝道三次计算取平均值得到的纵坡与L=-10时，匝道起点纵坡及方法四得到的匝道纵坡一致），见图2所示。

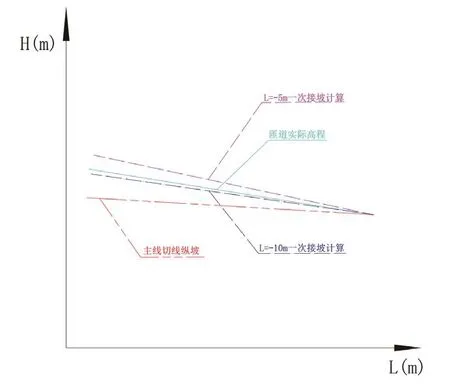
图2. 匝道起点接坡示意图

从图2可知，L=-5m时，匝道三次计算取平均值得到的纵坡、L=-10时，匝道一次计算纵坡及方法四得到的匝道纵坡更接近匝道实际高程，主线纵坡的切线坡误差最大。

总体而言，分、合流点位于主线直坡段，上述四种方法计算起点匝道的误差不是很大。当用于互通式立体交叉的施工图设计时，从考虑便捷与准确性而言，采用L=-10m进行一次接坡计算更快且更能保证顺接主线高程。如果用于立交的方案设计或者初步设计时，可直接用主线纵坡的切线坡，不考虑路面横坡与端部出入口角的影响。

（二）分、合流点位于主线竖曲线段

信州互通C匝道起点小鼻端N点（匝道纵断面设计起点）位于主线竖曲线内，竖曲线半径R=15000，前坡度为-1%，后坡度为1.3%。与上文一样，分别对L=-5m取一次计算和三次计算取平均坡进行对比分析。

表3. 信州互通匝道接坡计算中间数据（L= -5m）

通过计算发现L=-5m时，匝道起点纵坡i=-0.635%，三次计算取平均值得到i=-0.652%。将上述纵坡与主线对应的变速车道中心线的实际高程放在同一坐标系进行对比分析，见图3所示。

图3. L=-5m 匝道接坡示意图

由图3可知，当L=-5m时，匝道三次计算取平均值得到的结果更接近匝道实际高程，接坡更平顺。这主要是因为主线竖曲线上的点高程变化较缓，纵坡的两个点在竖曲线上距离很近，多次计算取平均值使得分、合流点更好地贴近鼻端前匝道纵坡。

分别对L=-10m取一次计算和三次计算取平均坡进行对比分析。

表4. 信州互通匝道接坡计算中间数据（L=-10m）

由表4可知，当L=-10m时，匝道起点纵坡i=-0.652%，三次计算取平均值得到i=-0.685%。

将上述纵坡与变速车道中心线的实际高程放在同一坐标系进行对比分析，见下图4所示。

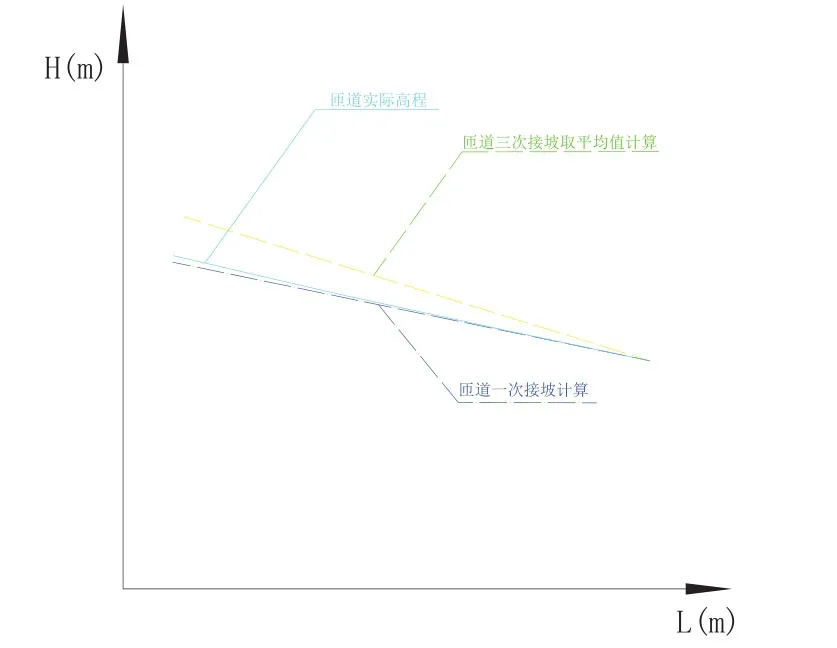
图4. L= -10m 匝道接坡示意图

由图4可知，当分、合流点位于主线竖曲线段，且L=-10m时，匝道一次接坡比多次计算取平均值更接近匝道实际高程，接坡更平顺。究其原因，笔者认为是因为两纵坡的取值点相距较远，多次取值反而误差更大。

第三种方法，采用主线纵坡的切线纵坡，匝道主线P点切线纵坡i=-0.532%，考虑主线横坡和切线方位角的影响，得到经修正后的匝道纵坡为i=-0.532% × cos2o-0.02× sin 2o=-0.532%。

将上述纵坡与主线对应变速车道的中心线实际的高程放在一个坐标系中进行对比分析（L=-5m时，匝道三次计算取平均值得到的纵坡与L=-10m时匝道纵坡一致；主线切线坡与修正切线坡一致），见图5所示。

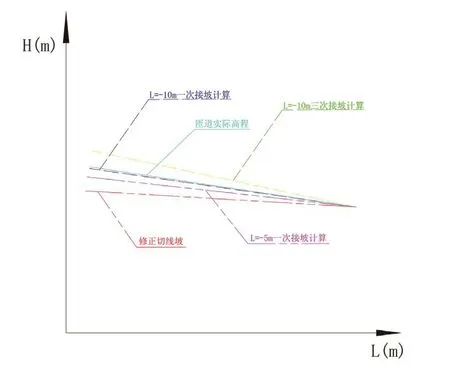
图5. 匝道起点接坡示意图

从图5可知，L=-10时，匝道一次计算纵坡与L=-5m时，匝道三次计算取平均值得到的纵坡更接近匝道实际高程，切线坡（含考虑方向角与横坡修正的的切线坡）误差最大。

总体而言，分、合流点位于主线竖曲线上时，采用主线的切线坡及修正切线坡误差最大，其他两种方法计算起点匝道的误差较小。当用于互通式立体交叉的施工图设计时，从考虑便捷与准确性而言，采用L=-10m进行一次接坡计算更快且更能保证顺接主线高程。如果用于立交的方案设计或者初步设计时，除切线坡方法（含考虑方向角与横坡修正的切线坡），其他几种方法均可。