TBM刀盘滚刀布置对倾覆力矩的影响规律

2020-05-21暨智勇夏毅敏兰浩杨妹林赉贶

中南大学学报（自然科学版） 2020年2期

暨智勇，夏毅敏，兰浩，杨妹，林赉贶

(1.中南大学高性能复杂制造国家重点实验室，湖南长沙，410083；2.中南大学机电工程学院，湖南长沙，410083；3.湖南师范大学工程与设计学院，湖南长沙，410008)

全断面岩石隧道掘进机(TBM)是一种用于隧道掘进的大型专用工程机械，刀盘、刀具是完成TBM 掘进施工的关键部件。刀具布置直接影响TBM破岩效果、刀盘力学性能和刀具消耗，同时，也对主轴承、推进和驱动系统的选型设计有重要影响，是刀盘结构设计的重要内容[1-3]。刀盘倾覆力矩作为刀盘重要载荷参数之一，是评价刀盘综合性能的关键参数之一，直接影响施工效率、施工成本和施工安全[4]，因此，探究刀具布置特征对刀盘倾覆力矩的影响规律具有很大的工程意义[5-7]。国内外学者就刀盘刀具布置对刀盘力学性能的影响进行了大量研究，如在理论分析方面，刘建琴等[8]建立了复合岩层下刀盘载荷模型，并探究了地质参数对载荷特性的影响规律；ROXBOROUGH等[9]提出了滚刀应对称布置于刀盘中心两侧，使其产生的切削力相平衡；张照煌等[10]基于刀具布置原则和滚刀破岩机理，提出了刀盘工作时的受力平衡理论，建立了基于刀盘受力平衡的滚刀布置数学模型。在数值模拟方面，程军等[11]采用智能算法开发了一种针对刀具布置的优化程序；曹旭阳等[12]基于刀具布置方法，编制了具有刀盘不平衡力和不平衡力矩数值显示功能的分析模拟软件；苏翠侠等[13]利用ABAQUS 软件动态模拟了刀盘切削土体的掘进过程，对不同掘进参数下刀盘载荷分布规律及其影响因素进行了研究；夏毅敏等[14]采用ANSYS 软件对不同工况下的3 种典型刀盘力学性能进行了对比分析。在优化算法方面，耿麒等[15-16]采用极径极角分别求解策略，对滚刀进行合理分组，采用加权灰靶决策方法筛选出最优方案；HUO 等[17]采用遗传算法、蚁群算法和协同进化算法求解刀具布置优化模型，对比分析算法的优劣；刘志杰等[18]提出了一种基于模糊逻辑推理和进化算法的刀具布置设计方法，得到最优刀具方案。综上所述，滚刀破岩受载产生的力矩是刀盘倾覆力矩的重要组成部分，通常刀盘倾覆力矩数学模型都是基于刀盘静态模式的前提下建立的，未考虑刀盘旋转破岩引起的倾覆力矩变化，也未对刀具布置影响刀盘倾覆力矩的原因进行分析。为此，本文作者研究刀具布置位置、倾角以及刀盘旋转角度因子对力矩的影响规律，建立考虑刀具布置位置、倾角以及刀盘旋转角度因子的倾覆力矩模型，分析单、双螺旋线刀具布置形式刀盘的中心滚刀、正面滚刀和边缘滚刀这3个布刀区域的倾覆力矩，并对其中1 个刀盘的刀具布置进行优化调整，以改善刀盘的力学性能。

1 刀盘倾覆力矩模型

1.1 单把滚刀载荷模型

刀盘上布置有多把滚刀用于切削破岩，承受掌子面对其的反作用三向力，RICHARD 等[19]提出了垂直力FV和滚动力FR的理论模型，夏毅敏等[14]提出了侧向力计算模型。

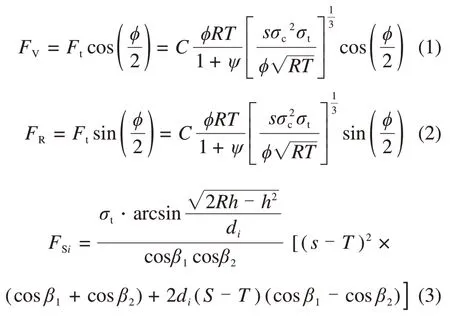
式中：FV为滚刀受到的垂直力；FR为滚刀受到的滚刀力；Ft为滚刀受到的合力；R为滚刀半径；T为滚刀刀尖宽度；h为滚刀贯入度；φ为滚刀与岩石接触角，ψ为刀尖压力分布系数，-0.2 ≤ψ≤0.2；s为两滚刀刀间距；σc为岩石的抗压强度；σt为岩石的抗拉强度；C为系数，C≈2.12；di为第i把滚刀在刀盘上的安装半径；β1和β2分别为第i把滚刀与其内侧、外侧滚刀间因相位差造成的岩面倾角。

1.2 刀盘倾覆力矩模型

刀盘总倾覆力矩主要由刀盘自重引起的力矩和刀具布置的不平衡产生的倾覆力矩叠加而成。

1.2.1 刀具布置产生的倾覆力矩

滚刀在切削岩石过程中产生三向力，其中，滚动力在刀盘运动的切线方向与倾覆力矩无关；侧向力与垂直力相比数量级很小，可忽略不计。本文只考虑垂直力产生的倾覆力矩。

假设刀盘上某一把滚刀受到载荷，该受力滚刀与刀盘中心点连线的垂线为倾覆力矩轴线，其水平线夹角为θi，刀盘空间角度为φ，如图1所示。滚刀受到的垂直力为FV，滚刀安装半径为di，并设定刀盘中心水平轴线为初始基直线。依据倾覆力矩计算规则，刀盘上受倾覆力矩在圆周范围内按照余弦函数规律分布，如图2所示。

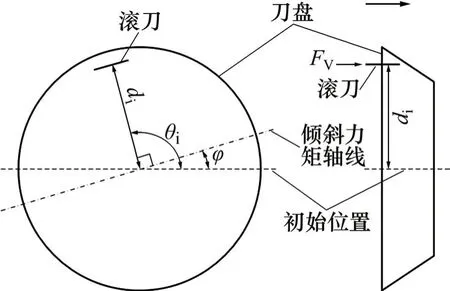
图1 单把滚刀施力示意图Fig.1 Load sketch map of a cutter

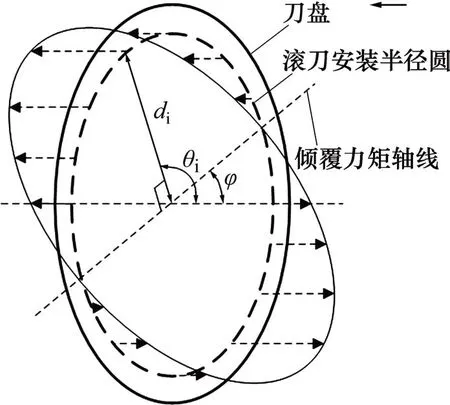
图2 单把滚刀力矩示意图Fig.2 Torque sketch map of a cutter

在刀盘空间角度下，由第i把滚刀引起的倾覆力矩的计算公式如下：

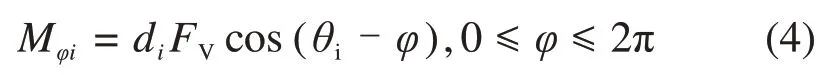
式中：Mφi为刀盘上第i把滚刀受力产生的倾覆力矩。若整个刀盘的全部滚刀受力，将具有不同布置位置和倾角的滚刀产生的倾覆力矩叠加到刀盘上，获得由刀具布置的不平衡产生的倾覆力矩为

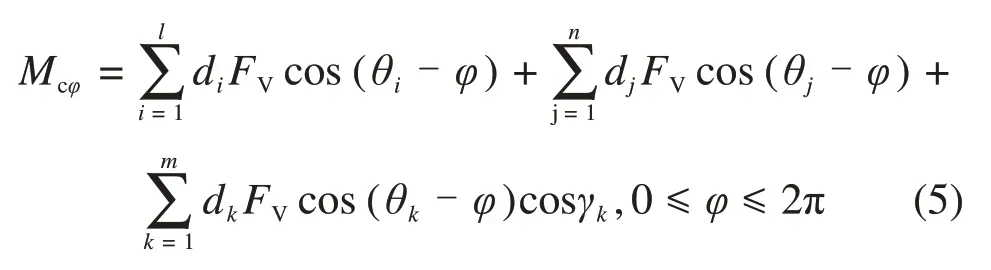
式中：Mcφ为整个刀盘全部滚刀受力后叠加在刀盘产生的倾覆力矩；l为中心滚刀的数量；n为正滚刀的数量；m为边滚刀的数量；γk为滚刀的安装倾角。

由式(5)可知，全部滚刀的倾覆力矩不仅与刀具在刀盘上安装位置(刀具安装半径、刀具安装角度)有关，而且与刀具受力有关。

1.2.2 重力产生的倾覆力矩

假设刀盘重力为GD，由Solidworks 三维模型得到刀盘质量，结合刀盘装配尺寸，可获得质心离刀盘与主轴承结合面的距离sd，如图3所示。sd不随刀盘转动而变化，得到刀盘自重产生的倾覆力矩公式如下：

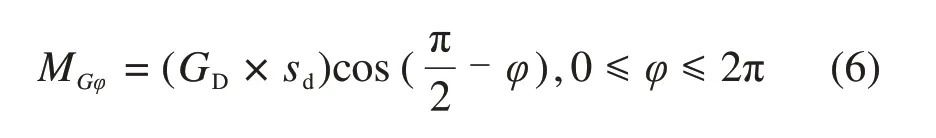
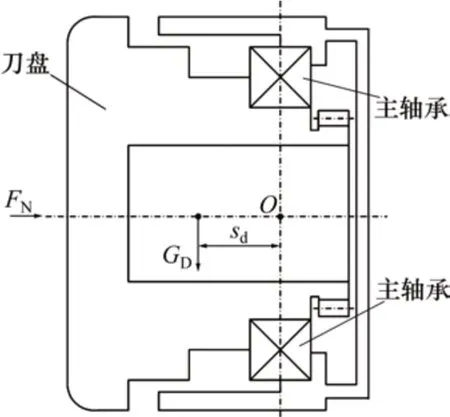
图3 刀盘自重产生重力矩结构Fig.3 Torque sketch map of cutterhead gravity

由式(6)可知，由刀盘自重产生的倾覆力矩与刀盘的尺寸、重力和质心位置有关。

刀盘总倾覆力矩为

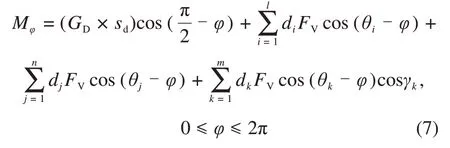
2 刀具布置形式对倾覆力矩的影响

刀具布置规律是影响刀盘整体性能的重要因素，盘形滚刀在刀盘上按一定力学和几何规律布置，分析典型刀具布置形式，对螺旋线刀具布置形式的刀盘倾覆力矩进行建模，并探究刀具布置对倾覆力矩的影响规律。

2.1 刀具典型布置形式

由于工程技术要求和地质条件不同，导致刀具的布局模式截然不同，因此，刀具布置方法还没有形成统一的设计方法和准则。典型的TBM 刀具布置方式有单螺旋线、双螺旋线布置、多螺旋线布置、动态星型布置和随机布置形式[20]，如图4所示。

2.2 螺旋线刀具布置的倾覆力矩计算模型

2.2.1 阿基米德螺旋线布置

阿基米德螺旋线也称为等速螺旋线，当一动点沿极径作匀速直线运动，并且极径本身又作匀角速度旋转运动时，这个动点的运动轨迹就称为“阿基米德螺旋线”，其极坐标可描述为

式中：a为螺旋线起始位置到原点的距离；θi为第i把滚刀的安装角度，取值为0~2nπ，n=1，2，3，…；A为常数。阿基米德螺旋线的螺距为2πA，如图5所示。

假设在1个360°循环内，平均分布n(n≥2)把正滚刀，将式(8)代入式(5)得

图4 典型刀具布置形式Fig.4 Layouts of typical cutters

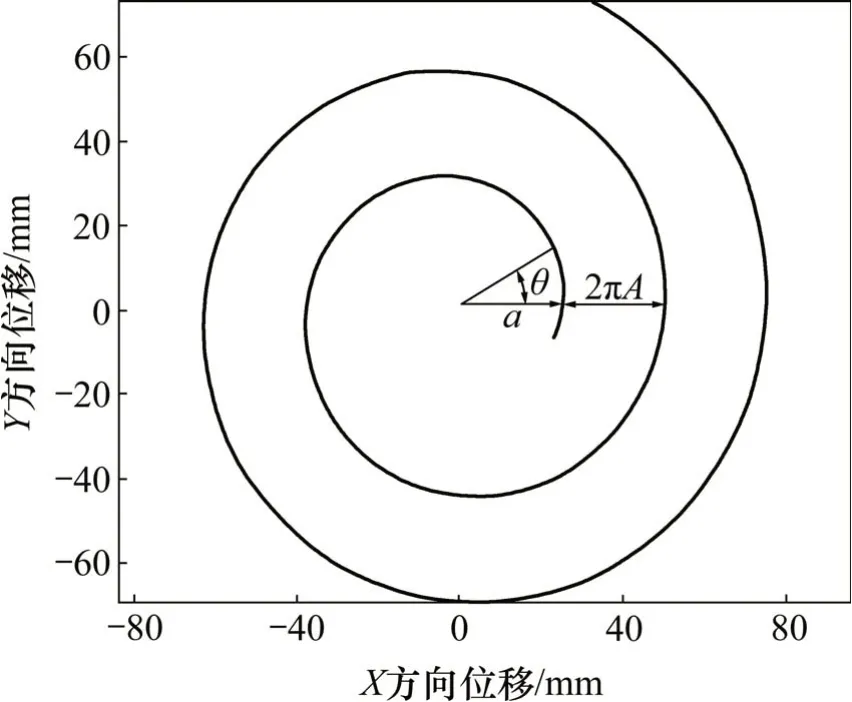
图5 单螺旋线轨迹Fig.5 Track of single spiral track

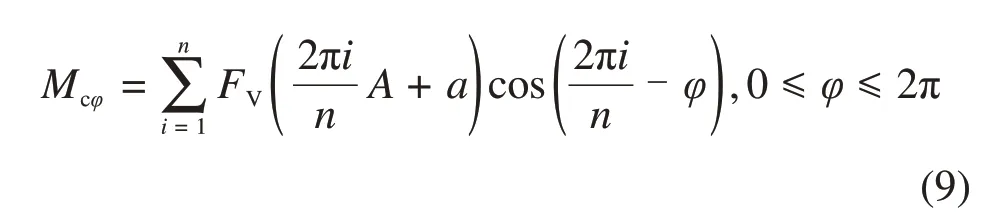
将式(9)展开如下：

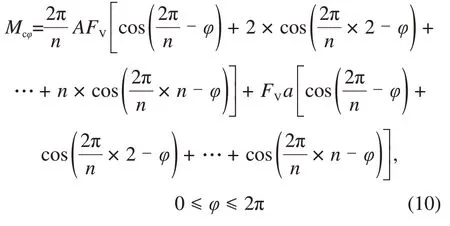
考察式(10)后半部分：

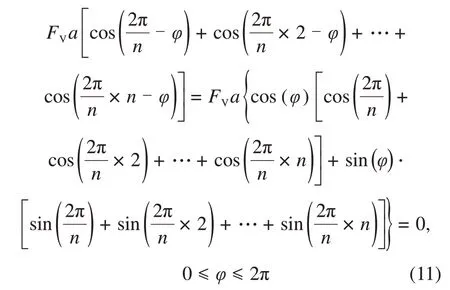
即式(10)后半部分为0，说明滚刀对称布置下倾覆力矩与起始位置的距离a无关，式(10)可简化如下：

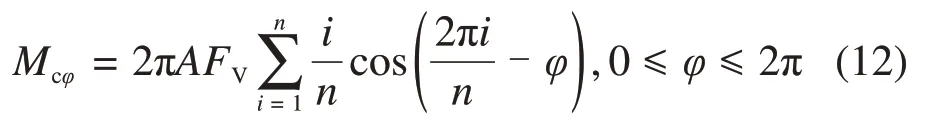
式(12)变形为

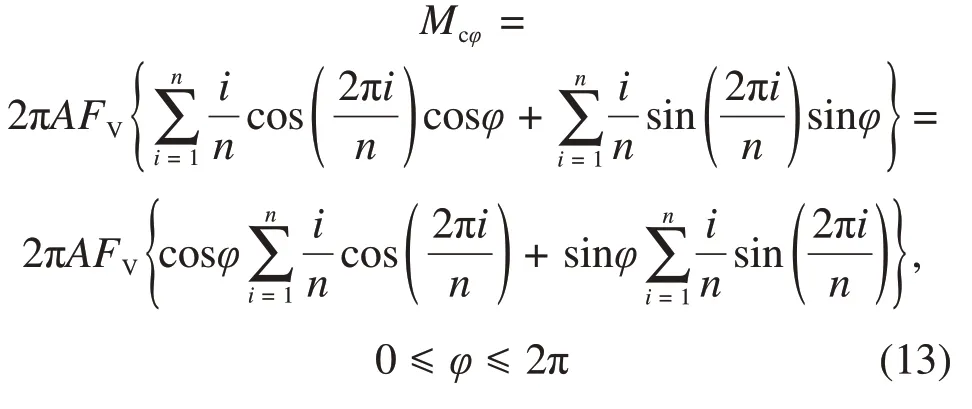
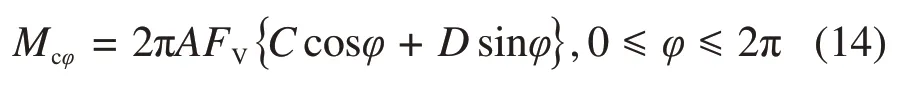
将式中Ccosφ+Dsinφ变换为

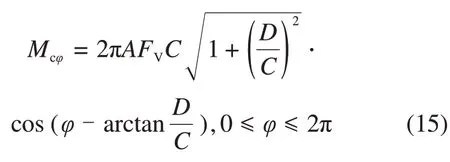
式中：2πAFVC′为倾覆力矩的幅值；cos(φ-)为倾覆力矩的角度因子。取cos(φ-)= 1的极值，得

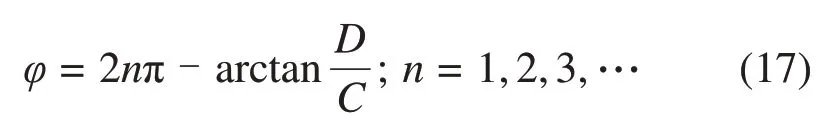
假设有m把滚刀，在每个360o循环内，当m为n的整数倍时，极径共旋转m/n圈，对式(9)变形得

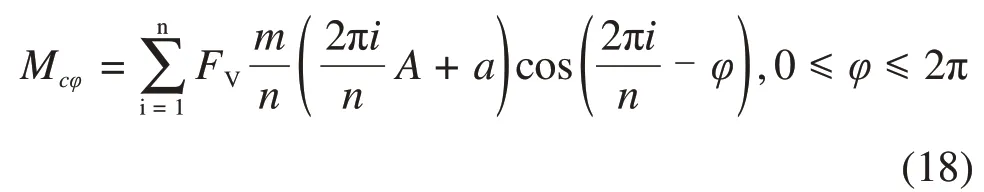
化简式(18)为

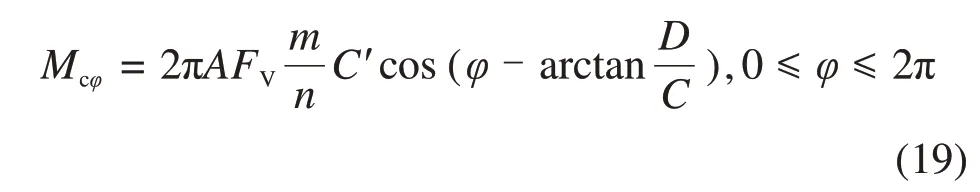
设s为正滚刀刀间距[21]，k为刀间距倍数，k=1，2，3，…，得2πA=k(n- 1)s，变形为A=，代入式(19)得

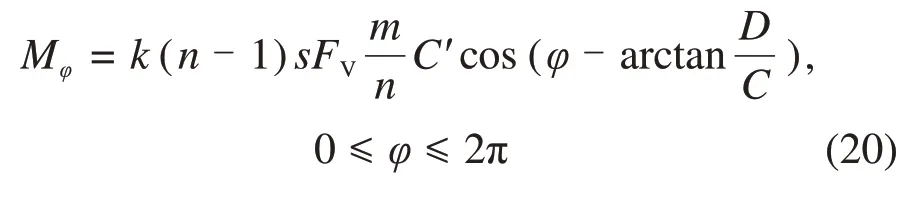
2.2.2 双螺旋线形式

有的刀盘进行刀具布置时采用双螺旋线布置，其轨迹如图6所示。

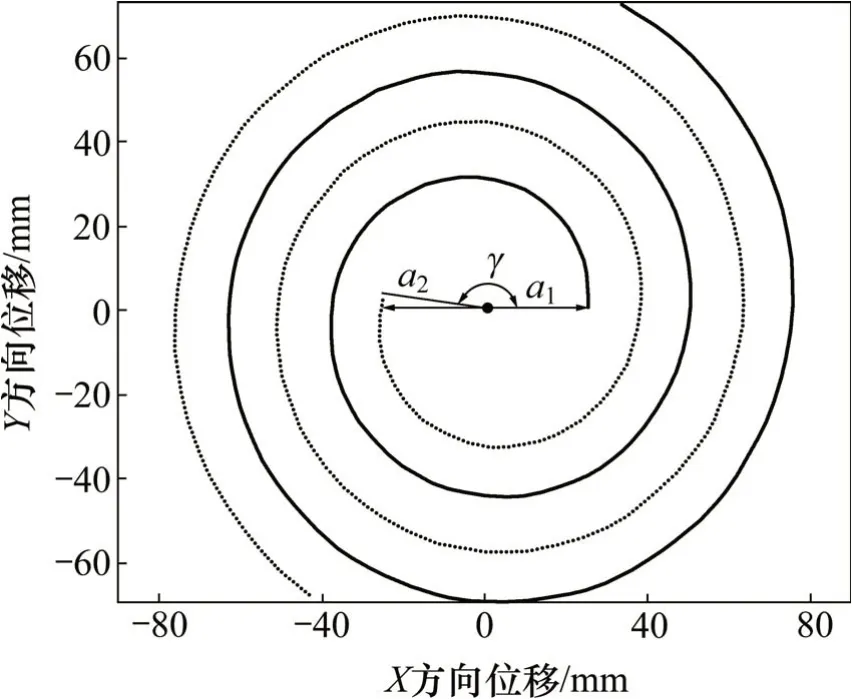
图6 双螺旋线轨迹Fig.6 Double helix trace

其螺旋线角度和半径满足公式：

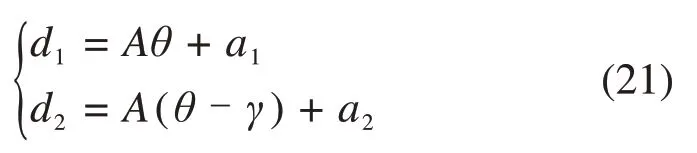
式中：a2=a1+ns；n=1，2，3，…；γ为2 条螺旋线起始位置相差角度。

假设有2m把滚刀分布在2条螺旋线上，2条螺旋线的上滚刀数量相等，若每条螺旋线极径转动一圈范围内，平均分布n(n≥2)把正滚刀，m为n的整数倍，代入式(20)并变形得

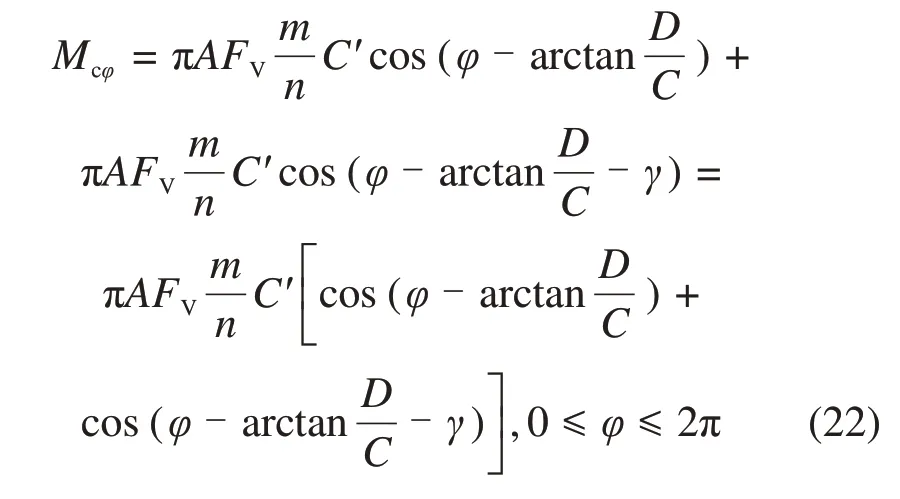
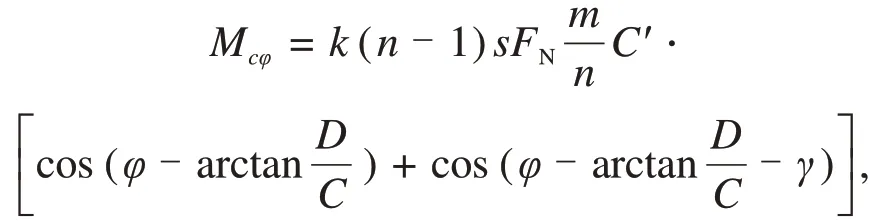
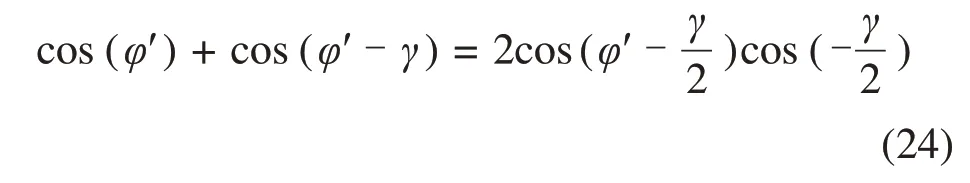
式(23)变形为

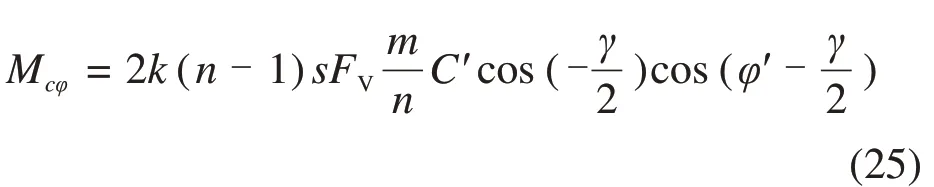
若刀具采用4条均匀的螺旋线布置形式，则可先选取对称的2条螺旋线叠加，再与其他螺旋线叠加的结果进行叠加运算。

2.3 螺旋线布置参数对倾覆力矩的影响

当n≥2时，采用一次函数拟合结果如下：

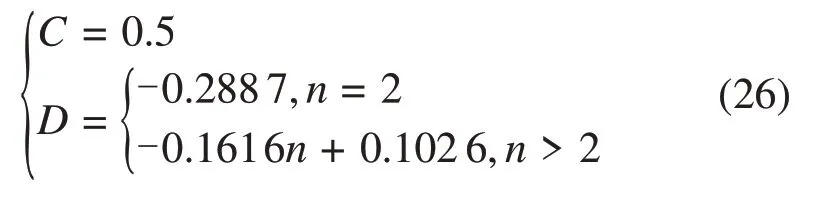
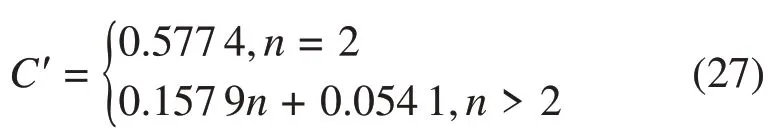
讨论倾覆角度与n的关系，由于C=0.5 和D<0，的取值在之间，因此，当满足时，φ取值在~2nπ之间。由式(17)所得倾覆角度与n的关系如图9所示。

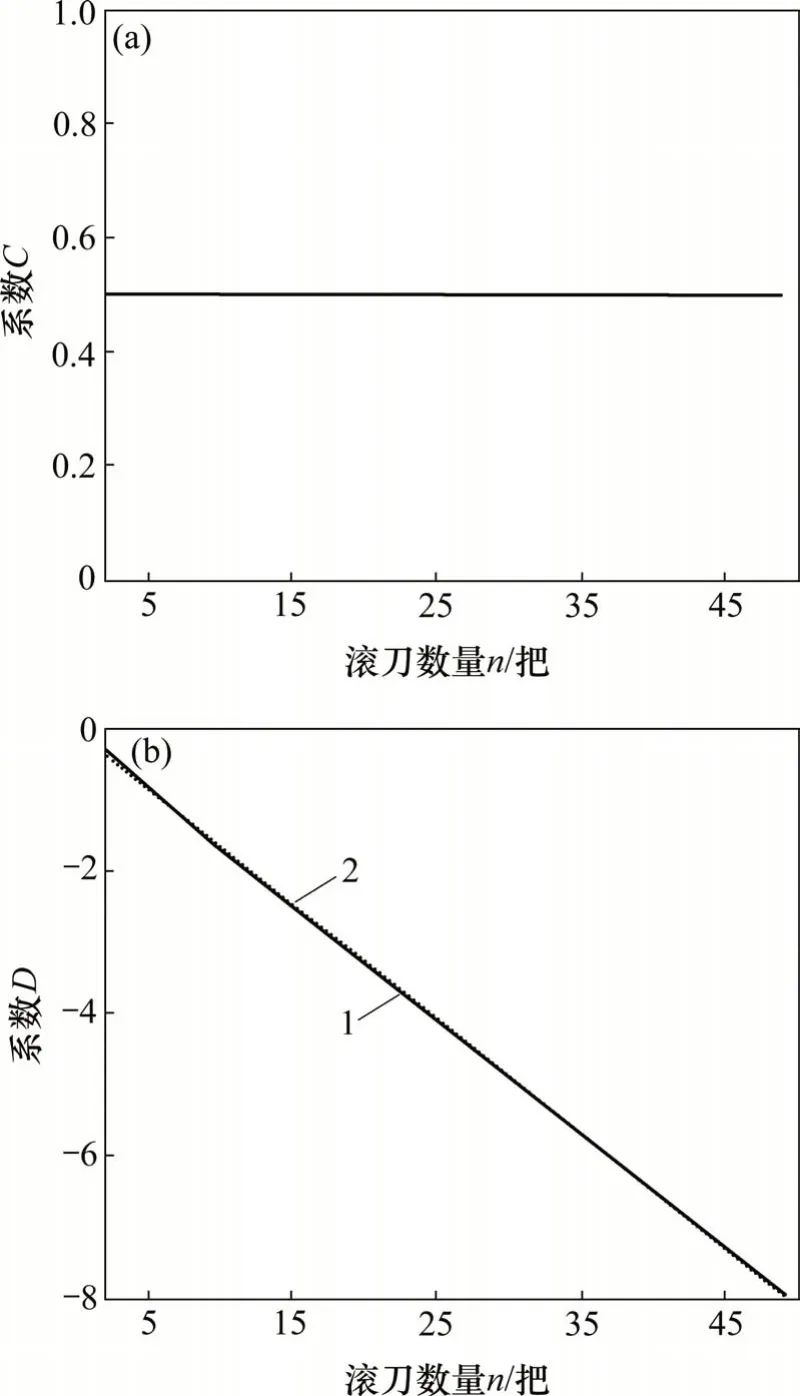
图7 C和D与n的关系Fig.7 Relationship betweenC,Dandn

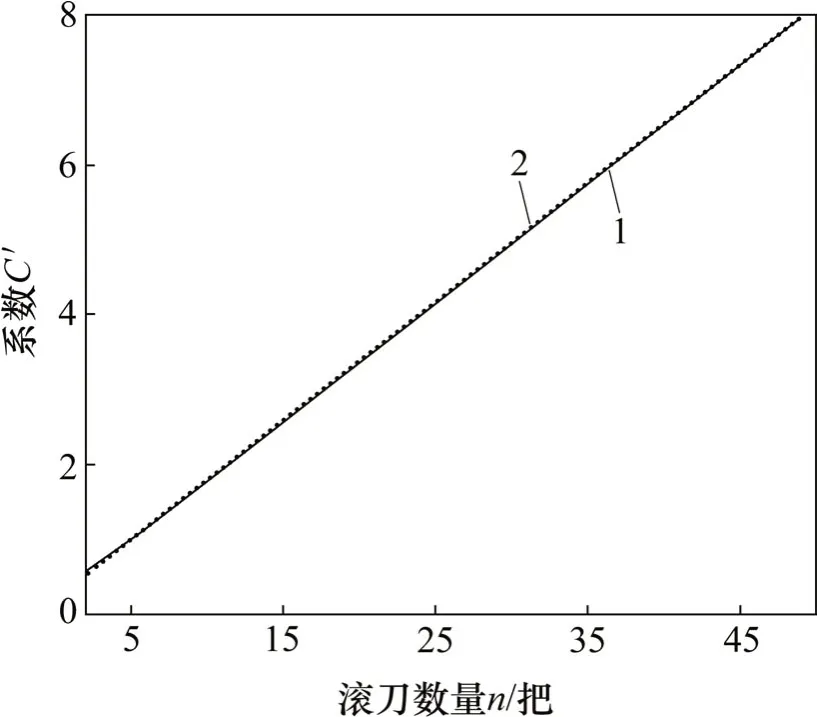
图8 C′与n的关系Fig.8 Relationship betweenC′andn

分析图9可知：1)若任意n(n>2)把刀布置在螺旋线上，则k取值为大于1 的正整数；2)若有2 个区间的刀具数量相同且布置位置不同，但当刀盘产生的倾覆力矩大小、方向、角度均相同时，则可认为这2 个区间的刀具可以相互等效。依此类推，若某一条螺旋线产生的倾覆力矩与另一些区域布置的刀具产生的倾覆力矩大小、方向、角度均相同，则可认为相互等效。

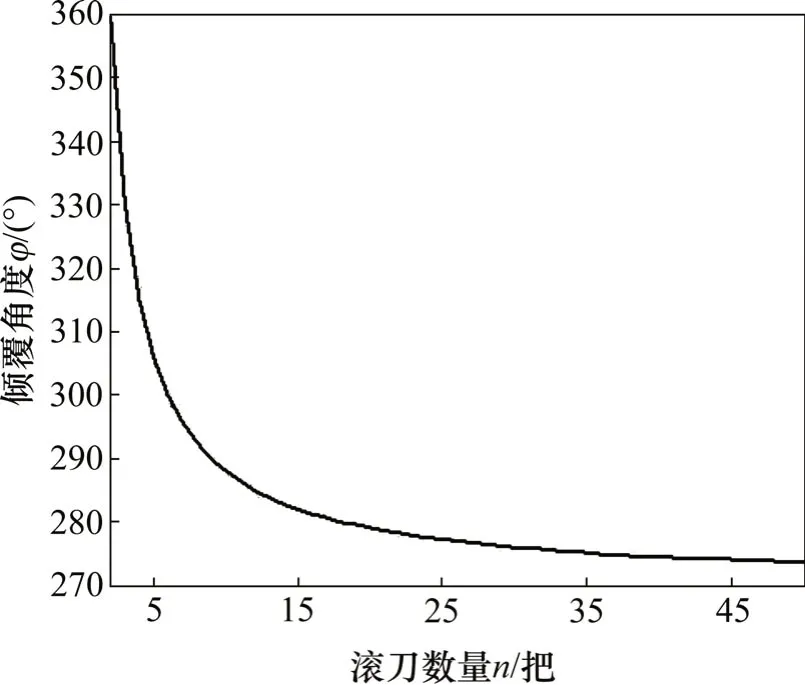
图9 倾覆角度与n的关系Fig.9 Relationship between angle of overturning andn

3 刀盘倾覆力矩分析及刀具布置优化

以典型工程案例的直径为8 m 级刀盘A，B 和C为研究对象，其刀具布置参数如表1所示。其中A 刀盘直径为8.53 m，滚刀刀刃数量为53 个，直径为483 mm，包括4 把双联中心滚刀(8 个刀刃)、32 把单刃正滚刀以及13 把单刃边缘滚刀，刀具采用双螺旋布置方案，中心刀的刀间距为100 mm，正刀的刀间距为90 mm；B刀盘直径为8.53 m，滚刀刀刃数量为53个，包括4把直径为432 mm的双联中心刀(8 个刀刃)、35 把直径为483 mm 的单刃正滚刀以及10 把直径为483 mm 的单刃边缘滚刀，刀具采用“米”字型布置，中心刀的刀间距为101.5 mm，正刀的刀间距为83 mm；C刀盘直径为7.93 m，滚刀刀刃数量为51 个，包括4 把直径为432 mm 的双联中心刀(8 个刀刃)、31 把直径为483 mm的正滚刀以及12 把直径为483 mm的单刃边缘滚刀，刀具采用“米”字型布置，中心刀的刀间距为101.5 mm，正刀的刀间距为83 mm。

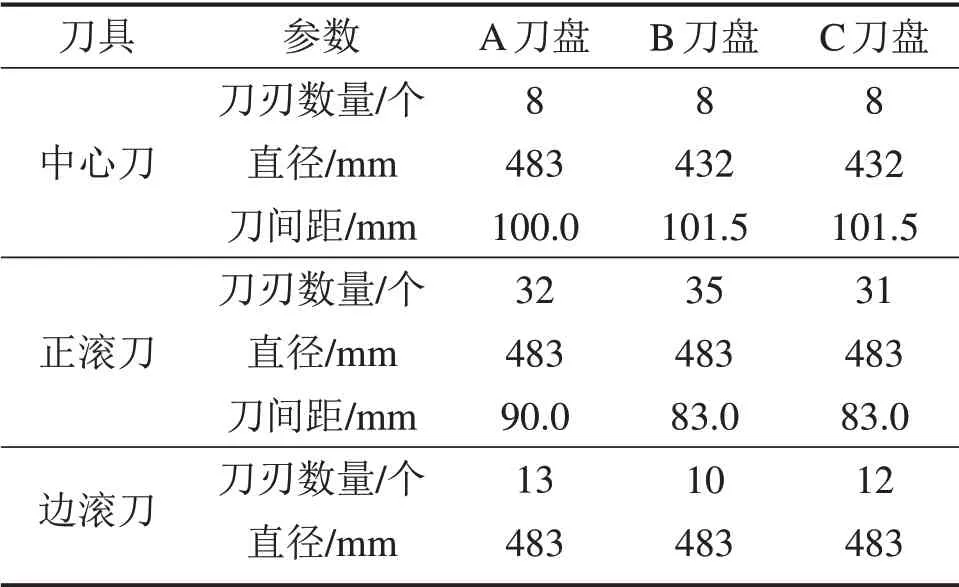
表1 3个刀盘的刀具布置参数Table1 Parameters of cutters’layout of three cutterheads

3.1 刀盘旋转角度对倾覆力矩的影响

以C 刀盘为研究对象，将刀盘按角度40°间隔依次顺时针旋转，分析刀具布置产生力矩和重力矩对倾覆力矩的影响，结果如图10所示。

从图10可见：当刀盘旋转角度为0°~120°时，倾覆力矩最大值随着角度发生变化，但当旋转角度为120°～240°时，倾覆力矩逐渐减少，为最大值的1/10，当旋转角度为240°～360°时，倾覆力矩重新回复到最大值；当刀盘旋转到一定角度区间时，由于刀具布置产生力矩和重力矩在作用方向相同时，呈现出力矩叠加现象。从图10(a)～(d)可见：当刀盘在0°～120°旋转时，其倾覆力矩的最大值为3 MN·m左右；刀具布置产生力矩和重力矩在作用方向相反，呈现力矩抵消现象。从图10(g)可见：当刀盘旋转角度为240°时，其倾覆力矩的最大值为0.24 MN·m左右。

3.2 刀盘在不同区域刀具的倾覆力矩分析

将刀具位置代入式(5)计算由刀具布置产生的倾覆力矩，按照中心滚刀，正滚刀，边滚刀这3个布刀区间计算3 个刀盘的倾覆力矩，结果如图11~13所示。

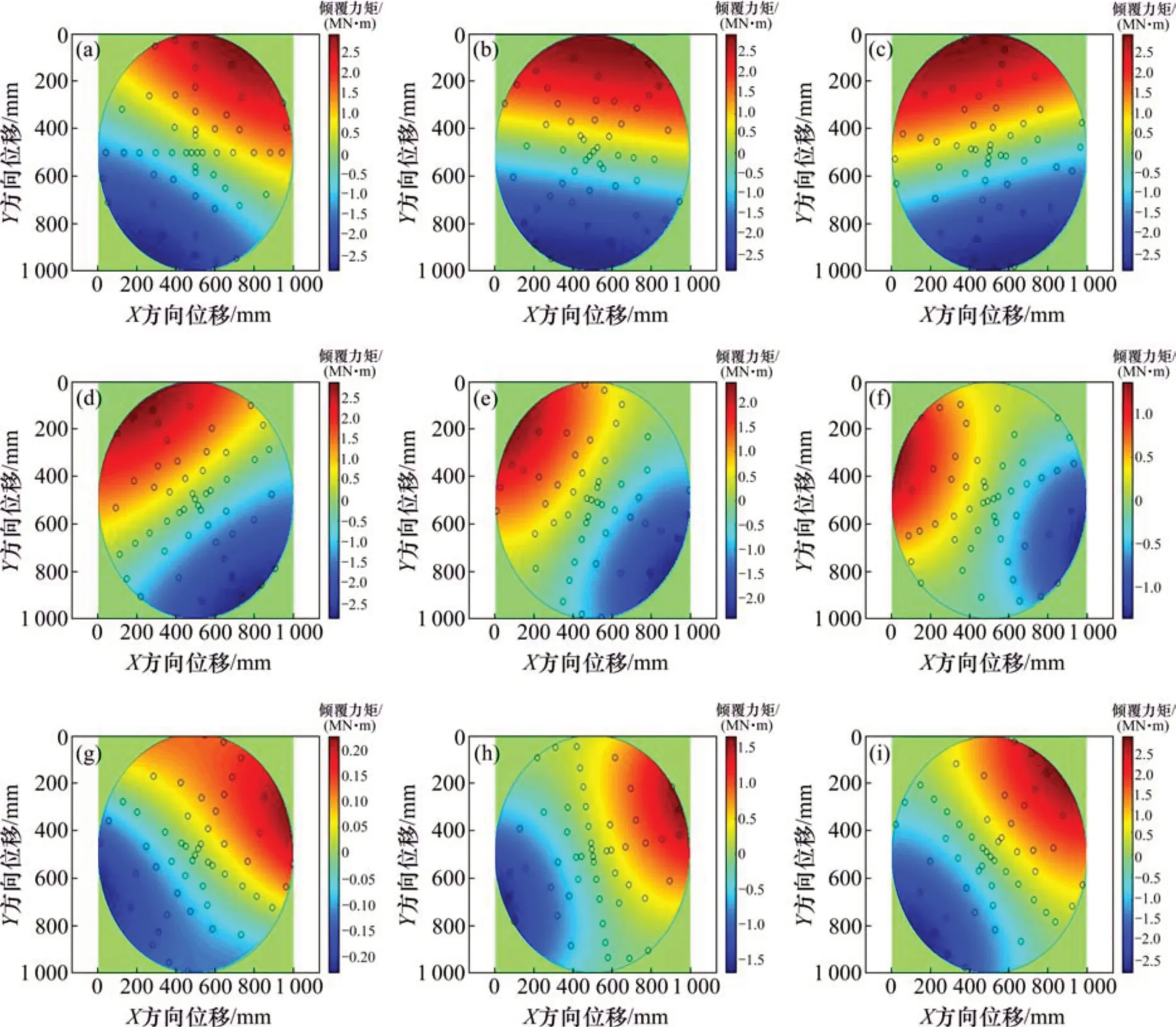
图10 C刀盘根据刀具布置和重力矩形成的倾覆力矩Fig.10 Overturning moments of cutterhead C

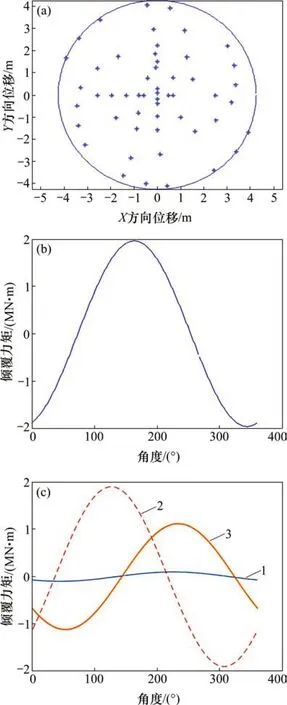
图11 刀盘A的倾覆力矩Fig.11 Overturning moments of cutterhead A

据图11~13可得出不同区间产生的倾覆力矩和角度，如表2所示。

对比A，B 和C 刀盘可以看出：A 刀盘在正滚刀区间呈非对称布置，B 和C 刀盘的布置相对对称；A 刀盘上的产生的倾覆力矩为1.954 MN·m，而B 和C 刀盘的倾覆力矩分别为1.585 MN·m 和1.440 MN·m；A 刀盘由于刀盘布置产生的倾覆力矩是C刀盘的1.36倍，是B刀盘的1.23倍。

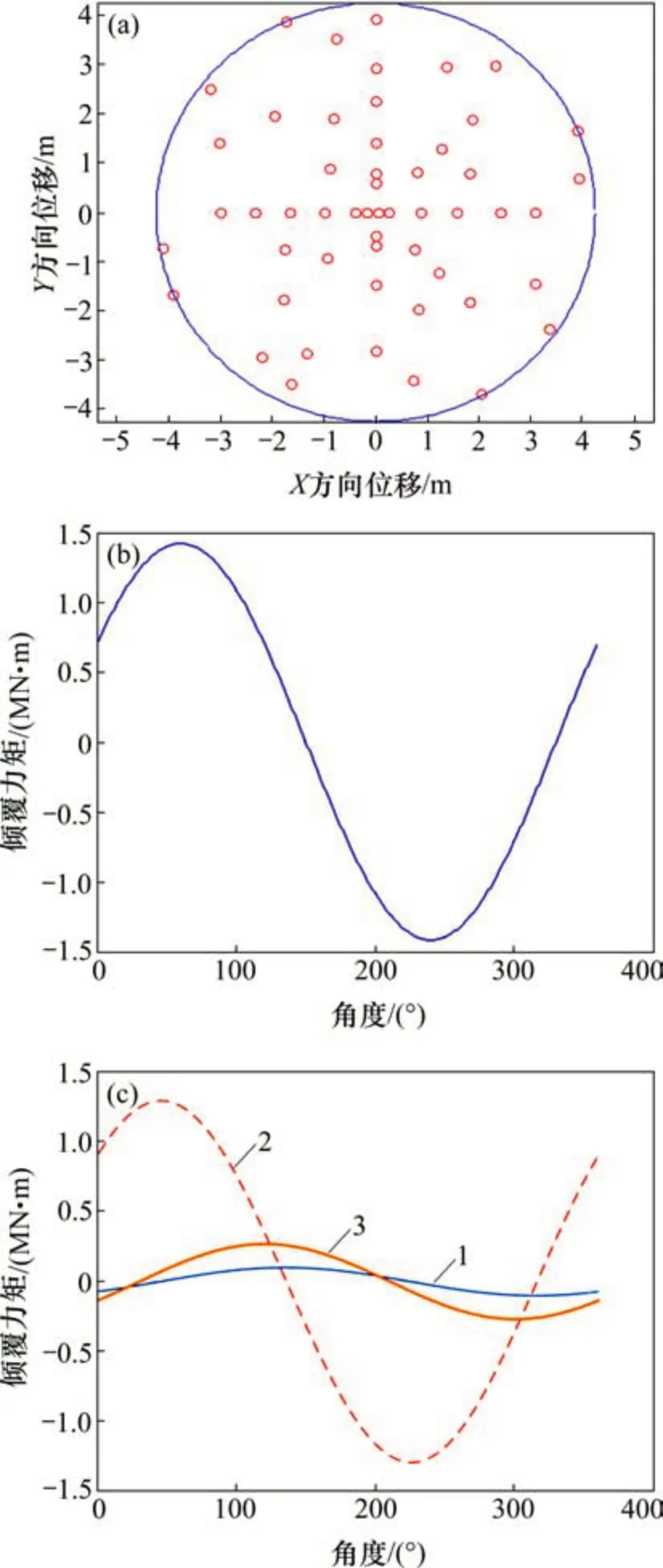
图12 刀盘B的倾覆力矩Fig.12 Overturning moments of cutterhead B

从表2可以看出：由于中心刀数量很少，A，B和C刀盘均为8把，其倾覆力矩均为0.10 MN·m左右，占总倾覆力矩的5%；正滚刀布置数量多，且滚刀的安装半径较大，占总倾覆力矩的70%~85%；而边滚刀由于受倾角的影响，实际施加的垂直力变小，占总倾覆力矩的10%~25%，导致这种较大差别的原因是：

1)在边滚刀布置上，A刀盘采用2条螺旋线相对集中布置在2个区间，而B和C刀盘相对均匀分布在刀盘的四周，因此，A刀盘产生的倾覆力矩分别是B和C刀盘的4倍和2倍；

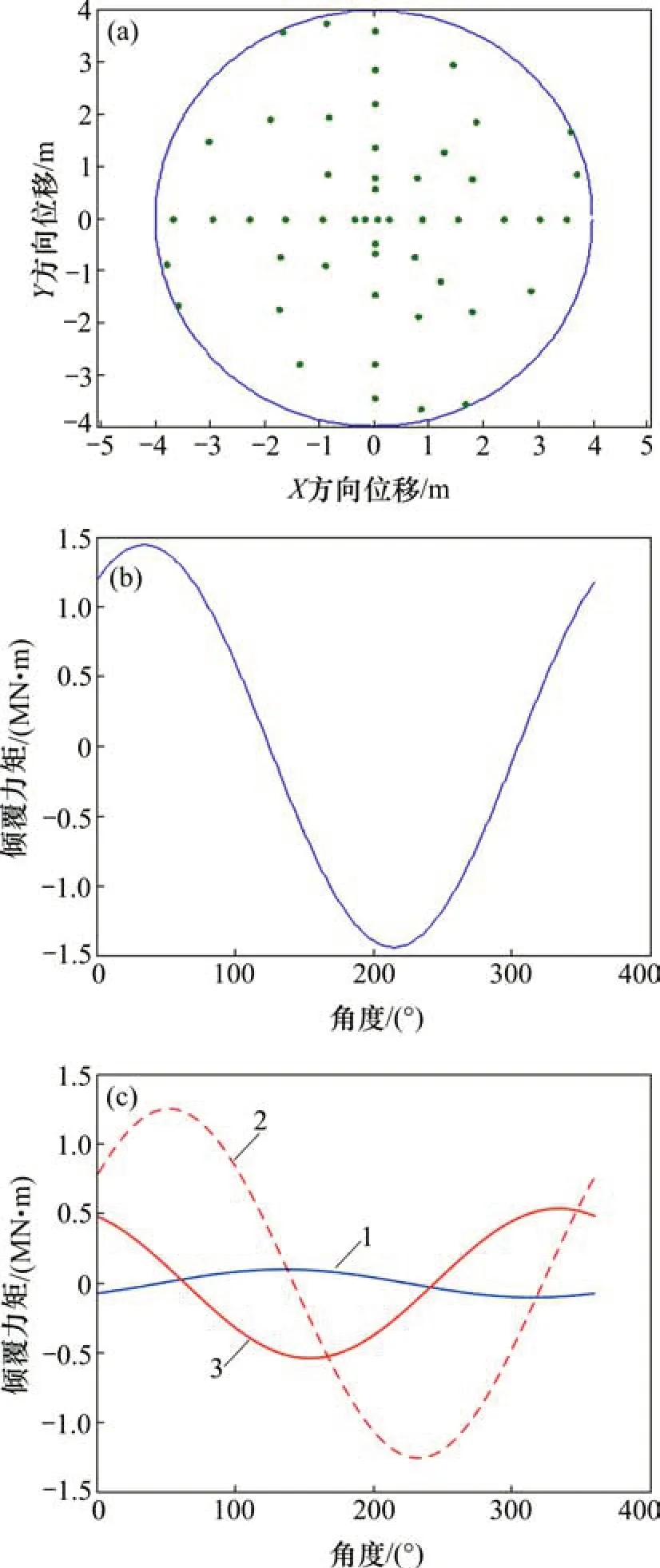
图13 刀盘C的倾覆力矩Fig.13 Overturning moments of cutterhead C

2)在正滚刀布置上，A刀盘随机分布，B和C刀盘采用对称布置，使A刀盘产生的倾覆力矩比B和C刀盘大1.47倍和1.51倍。

3)正滚刀在刀盘中间依据水平轴和垂直轴布置，因此，产生倾覆力矩角度相差过小，但正滚刀和边滚刀的布置使A 刀盘的正滚刀和边滚刀倾覆力矩角度差为107°，而B 和C 刀盘分别为75°和77°。

3个刀盘自重产生的重力矩如表3所示。

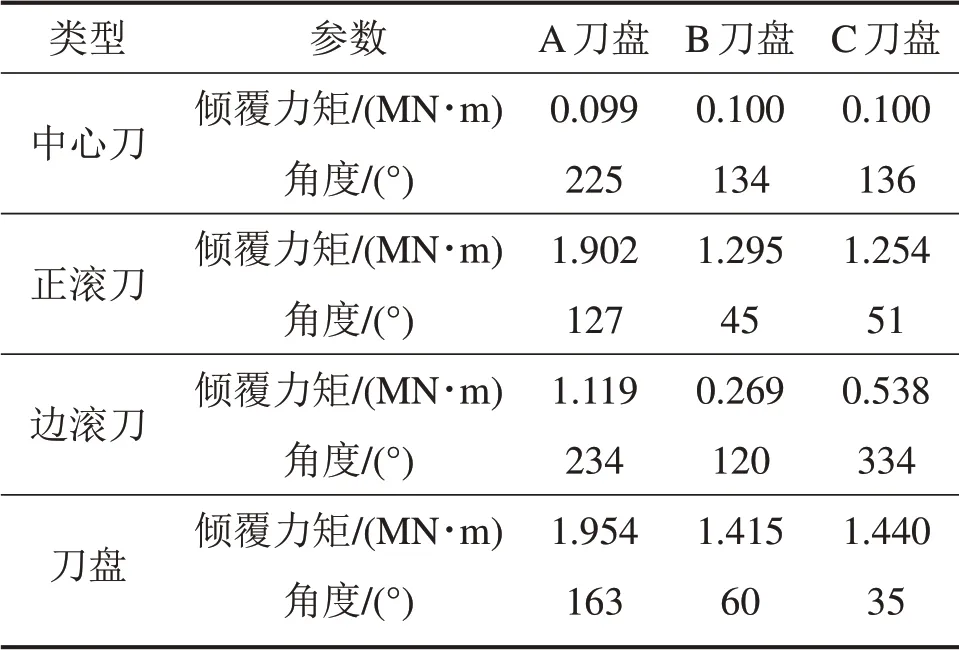
表2 3个刀盘不同区域刀具产生的倾覆力矩和总倾覆力矩Table2 Overturning moment and total overturning moment generated in different areas of three cutterheads

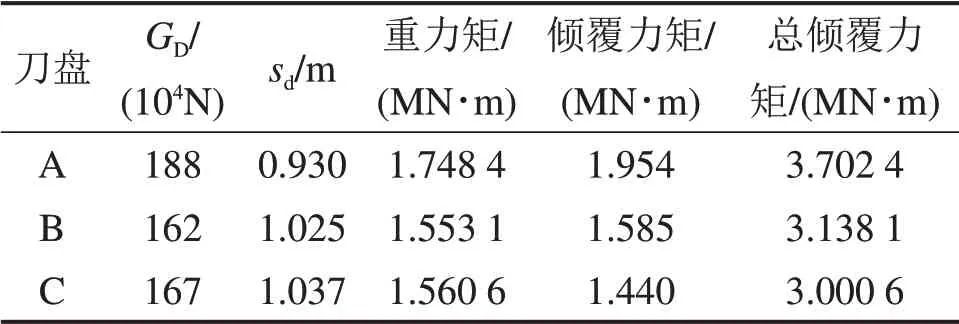
表3 刀盘自重产生的总倾覆力矩Table3 Total overturning moment

3.3 工程应用

由于TBM 在掘进施工过程中面临随机多变的地质环境，刀盘掘进性能无法全面准确评价，其中刀具消耗数量、故障率主要是由于刀盘刀具受载特性决定，而刀盘刀具关键载荷参数即倾覆力矩与刀具布置参数密切相关，因此，通过实际TBM 隧道施工过程中刀具消耗数量、故障率分析间接评价刀盘滚刀布置方案的合理性和地质适应性。

3.3.1 基于倾覆力矩的刀具布置优化

由式(25)可知，通过调整阿基米德螺旋线起始相位角度以调节幅度关系函数式(25)中的角度γ，即调整倾覆力矩最大值所在的相位，通过螺旋线对称时产生的倾覆力矩叠加相互抵消，进而减少倾覆力矩。设定正滚刀和边滚刀由2 组螺旋线组成，分析C刀盘可发现正滚刀和边滚刀区域产生倾覆力矩的角度分别为334°和51°，相差283°。将边滚刀布置位置都后移90°，即44～51 号刀(8 把)在保证安装半径和倾角不变的情况下，将此8把边滚刀的原始角度减90°。改变前后刀盘位置，如图14(a)所示；由刀具布置产生的倾覆力矩如图14(b)所示，3 个布刀区间产生的倾覆力矩如图14(c)所示。

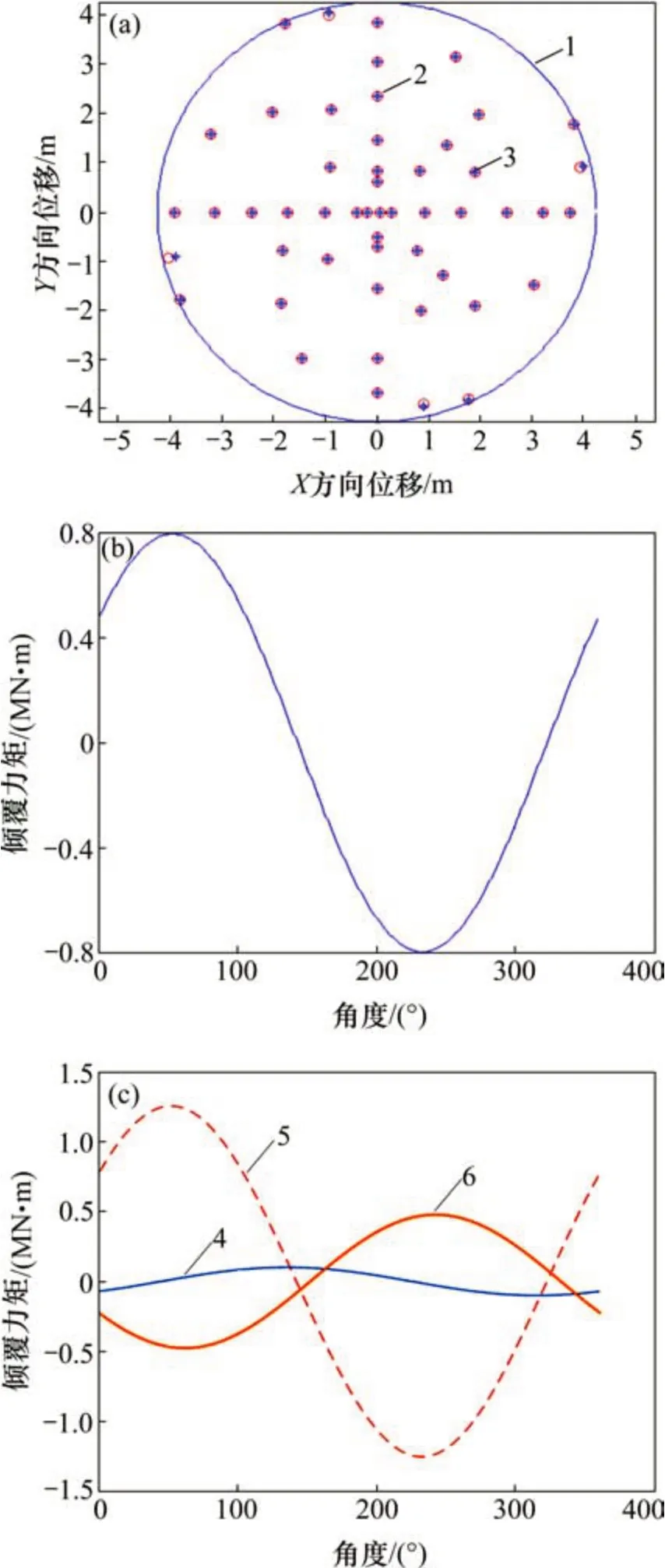
图14 改进后刀盘C的倾覆力矩Fig.14 Improving overturning moment of rear cutter C

从图14可见：改进后的边滚刀倾覆力矩的角度由334°减小为242°，与正滚刀区域产生的倾覆力矩角度51°相差191°；改进前后测算的倾覆力矩从1.440 0 MN·m 减少到0.794 7 MN·m，减少44.8%；若考虑刀盘自重，则总倾覆力矩为2.355 3 MN·m，比原设计的3.000 6 MN·m减少0.640 0 MN·m，仅为原先倾覆力矩幅度的78.6%。

3.3.2 工程应用

将C刀盘优化结果运用于实际供水隧道工程用的TBM 刀盘中，最终确定的刀盘方案如图15所示。刀盘上安装有51 把滚刀，其中，有8 把直径432 mm双刃滚刀，刀间距为101.5 mm，布置在刀盘中心区域；有32把直径为483 mm的滚刀，刀间距为83 mm，布置在刀盘正面区域；有11 把直径为483 mm的滚刀布置在刀盘边缘区域。

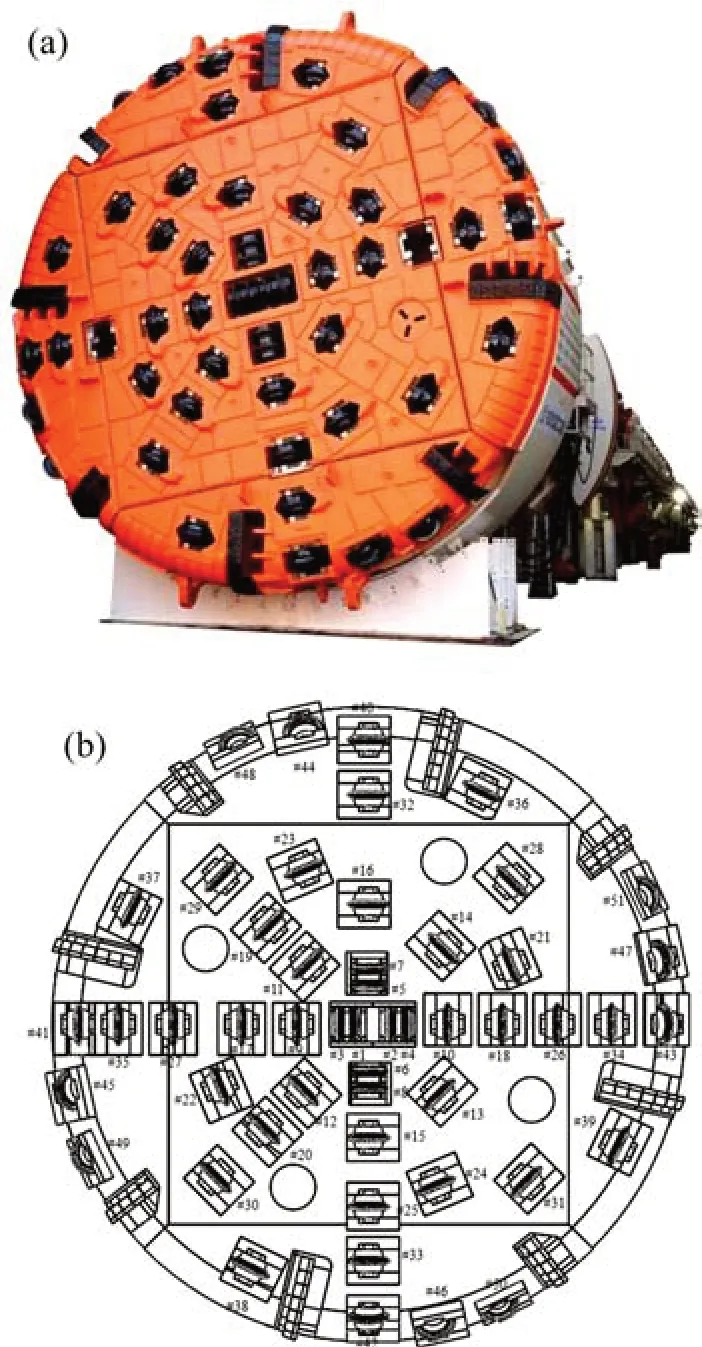
图15 优化后的C刀盘模型Fig.15 Real cutterhead C models after optimization

该TBM 在7月份工期内，掘进岩层稳定性等级为Ⅱ—Ⅳ类，岩石较硬，石英质量分数为25%，其中Ⅱ类岩层占比在70%以上，且中间存在断层带。对该供水隧道工程在7月份工期内的掘进量、刀具更换数量、故障次数和故障率进行统计分析，结果如表4所示。

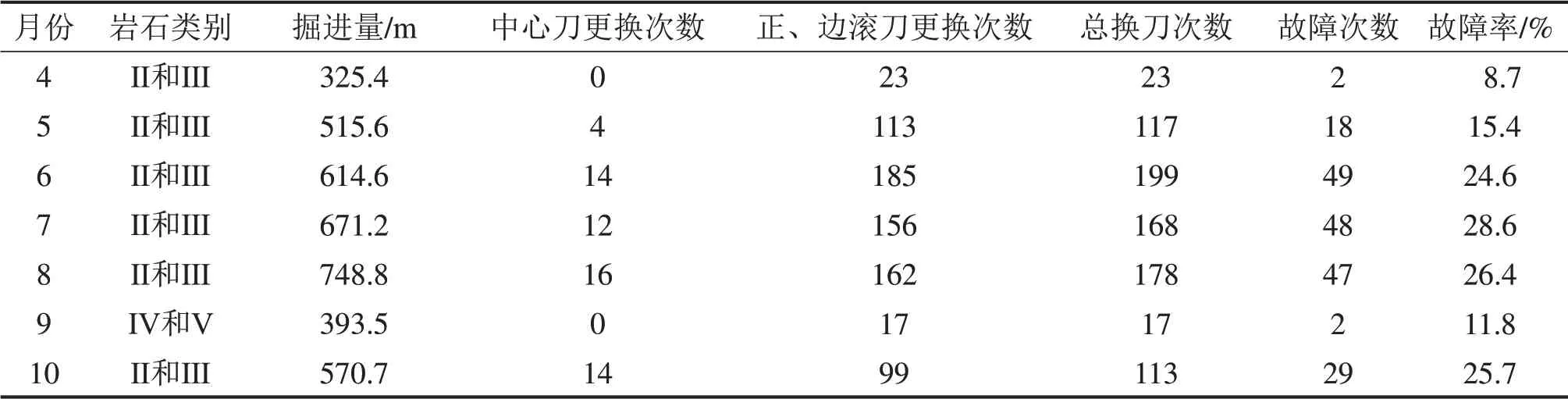
表4 C刀盘掘进性能数据Table4 Tunneling performance data of cutterhead C

由表4可知：在Ⅳ和Ⅴ岩层，TBM的掘进速度比Ⅱ和Ⅲ岩层慢，4月至10月累计掘进里程为3 839.8 m；换刀量最大为6月份，总换刀次数为199 次；4月份由于只掘进18 d，同时岩层较软，换刀次数为23 次；9月份由于掘进岩层处于断裂带，岩石较软，换刀次数为17 次。合计中心滚刀更换60 次，正面滚刀和边缘滚刀更换755 次，总换刀次数为815次；工期内因故障换刀195次，其中6月份故障换刀次数最高，为49 次，而故障率最高为7月份，为28.6%。故障形式包括刀圈偏磨、刀圈崩断、刀具漏油、刀体受损、刀轴断裂和刀具高温。

综合分析工程结果可知：刀盘的掘进速度满足施工进度要求，换刀次数远小于其他工程刀盘的换刀次数；从4月份到10月份，故障率都低于30%，属于正常稳定状态，因此，该TBM 刀盘刀具布置形式基本满足设计要求。