TBM空间管道动态特性分析

孙文倩，张怀亮，瞿维，熊宇

(1.中南大学高性能复杂制造国家重点实验室，湖南长沙，410083；2.中南大学机电工程学院，湖南长沙，410083)

液压系统是TBM(硬岩掘进机)重要的能量传递和控制系统，其工作性能是决定TBM 掘进效率和安全的重要指标[1]。空间管道是液压系统的主要元件之一，在强振动环境下，一方面，外界基础振动传递给管道能量，导致管道位移变形量增大，管壁产生的应力剧增，从而使管道出现疲劳破坏；另一方面，由于流固耦合作用，由管道传递到流体的能量造成管内流体和压力发生较大波动，因此，有必要对基础振动下空间管道的动态特性进行分析。PAIDOUSSIS 等[2]认为管内流体会使管道产生振动，由此输流管道振动的相关问题逐渐引起了人们的关注。FEODOS’EV 等[3-4]建立了两端支撑的单跨输流管道运动的线性方程，发现当管内流速超过临界流速时会使管道失稳。LEE等[5]推导了输送简谐脉动流体的三维管道系统的运动方程，提出了一种预测管道系统稳态时间响应的有效数值方法。WADHAM-GAGNON 等[6]研究了限制性和非限制性流体传递管道的三维非线性问题。SREEJITH 等[7]将全耦合的方程应用到核工程管道中，以流速为变量建立管道的有限元模型，研究了管道的速度响应特性。MENSHYKOVA等[8]对复合层管道的应力分布进行了研究，分析了不同结构参数下复合管道应力的变化规律。NIKOLIĆ等[9]分析了不同非线性模型的两端固支输流管道，得到了各模型的超临界和亚临界分叉发生的条件。KHEIRI 等[10]运用拓展的Hamilton 原理建立了一端弹簧支撑一端自由轴向流动的平动圆柱柔性管道的线性动力学方程，并分析了无振动刚体的不稳定性。JIN 等[11]运用数值求解的方法研究了输流管道的稳定性和参数共振问题，分析了阻尼、平均流速以及质量比等物理参数对管道共振区域的影响。杨飞益[12]研究了两端固支空间管道系统的动态响应特性，运用有限元软件得到了空间管道最大应力随管内流体流速和卡箍数的变化规律。黄益民等[13]通过把支撑简化为集中质量和约束3个方向位移和旋转的弹簧，研究了支撑刚度对输流管系动力学特性的影响规律。付永领等[14]研究了弯管的弯曲角度对输流管道振动特性的影响规律。俞树荣等[15]运用有限元分析软件进行了双向流固耦合受力分析、单双向流固耦合对比分析和模态分析,并考虑了脉动压力、壁厚和管径等参数的影响。杨超[16]研究了非恒定流下管道系统的流固耦合特性，推导了弯管的流固耦合振动方程，分析了弯管的振动力学特性。苟兵旺等[17]推导了基础振动下两端简支输流管道的数学模型，对支撑激励下管道的动态特性进行了分析。HUANG等[18]运用伽辽金法对不同边界条件下管道的固有频率进行求解，并发现科里奥利力对管道固有频率影响很小。梁峰等[19]利用多元L-P法研究了外部周期激励下两端固定输流管道伴随内共振的非线性受迫振动问题。刘森等[20]采用特征线法对基础振动下TBM 液压弯管管内流体的波动进行了研究，得到了基础振动下弯管的支撑方式、振动参数、结构参数对弯管动态特性的影响规律。瞿维等[21]利用双向流固耦合的方法建立了流体域和固体域的仿真模型，研究了不同基础振动参数和弯管的结构参数对弯管动态特性的影响规律。综上所述，国内外对管道振动特性的研究主要集中在管道自激振动分析上，而外激励作用下管道动力学方面的研究较少，且主要集中于直管和弯管，对空间管道的研究较少，为此，本文作者应用有限元分析与试验验证相结合的方法研究强振动环境下空间管道的动态特性。

1 仿真建模

1.1 几何建模及网格划分

假设空间管道为均质、纯弹性及各向同性的等截面圆管，管内的流体做低速运动，且不存在摩擦效应，忽略流体中的体积分离、气穴等现象。根据TBM 现场考察资料，设定管道材料属性与管内液压油参数如表1所示。空间管道三维模型以及进行网格划分后的管道模型和流体模型分别如图1和图2所示。

1.2 边界条件设置

设置流固耦合接触面(fluid solid interface)为管道内壁。管道采用两端固支的支撑方式，通过两端支撑传递给管道的激励采用正弦位移载荷。在CFX 里面设置流体域，流体外壁设置为流固耦合接触面，沿Y轴方向设置为流体进口(inlet)，沿X轴方向设置为流体出口(outlet)，如图3所示。

表1 管道系统相关参数Table1 Related parameters of piping system

图1 空间管道三维模型Fig.1 3D model of space pipeline

图2 管道和流体的网格划分Fig.2 Meshing of pipeline and fluid

图3 流体边界Fig.3 Fluid boundary

2 有无基础振动时管道动态特性

仿真时设置基础振动幅值为1 mm，频率为60 Hz，振动方向为Y向振动，得到有无基础振动时两端固支空间管道应力云图和出口压力波动响应图，如图4、图5和图6所示。由图4和图5可知：有基础振动时管道最大等效应力约为81.62 MPa，而无基础振动时管道的最大等效应力为49.99 MPa，说明有基础振动时管道应力会明显增加，容易造成应力疲劳破坏。由图6可知：有基础振动时管道的出口压力波动幅值显著增加，其出口压力波动幅值是无基础振动时管道出口压力波动幅值的3.98 倍。由上述研究可知：外界基础振动对管道动态特性有很大的影响，在实际工作过程中不能忽略。

图4 有基础振动时管道等效应力云图Fig.4 Equivalent stress cloud diagram of pipeline with basic vibration

图5 无基础振动时管道等效应力云图Fig.5 Equivalent stress cloud diagram of pipeline without foundation vibration

图6 有无基础振动管道出口压力波动响应Fig.6 Pipeline outlet pressure fluctuation response with or without basic vibration

3 空间管道应力分析

3.1 振动参数对应力的影响

管道流固耦合仿真结束后，将仿真结果导入static structural 模块与model 模块进行含预应力的管道模态频率分析，得到不同方向振动下管道一阶模态频率，如表2所示。

结合TBM 实际工作情况，设置基础振动幅值为1 mm，基础振动频率f为20~200 Hz，仿真分析不同方向振动下管道最大应力随基础振动频率变化的规律，结果如图7所示。由图7可知：当外界基础振动频率靠近管道模态频率时，管道的最大应力会增加；当20≤f＜120 Hz时，X向和Y向振动在振动频率为100 Hz 时管道最大应力最大，因为此时基础振动频率接近管道一阶和二阶模态频率，并且X向与Y向振动作用下的管道最大应力高于Z向振动下的管道最大应力；当120＜f≤200 Hz 时，X向、Y向和Z向振动均在振动频率为160 Hz 时，管道应力最大，因为此时基础振动频率接近管道三阶模态频率；Z向振动下管道的最大应力大于X向与Y向振动下管道的最大应力，前者约为后者的4.12倍，故当120≤f≤200 Hz时，应避免Z向振动。

表2 不同方向振动下管道一阶模态频率Table2 First-order modal frequency of pipeline under different vibration directions Hz

图7 管道最大应力随基础振动频率的变化Fig.7 Change of the maximum stress of pipeline with fundamental vibration frequency

设定基础振动频率为60 Hz，基础振动幅值为0.5~1.5 mm，仿真得到振动方向为X向、Y向和Z向时不同基础振动幅值下管道的最大应力，如图8所示。由图8可知：当基础振动频率一定时，管道最大应力随着基础振动幅值的增大而增大。这是因为基础振动幅值越大，使得外界输入到管道能量越多，导致管道振动加剧。与X向和Y向振动相比，Z向振动下管道最大应力增加的速率最小，即当基础振动频率为60 Hz 时，Z向振动对管道最大应力的影响最小。

3.2 结构参数对应力的影响

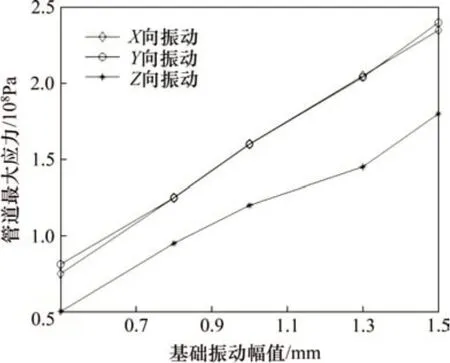
图8 管道最大应力随基础振动幅值的变化Fig.8 Change of the maximum stress of pipeline with amplitude of fundamental vibration

设定基础振动幅值为1 mm，振动频率为60 Hz，仿真分析不同中间直管长度、管道内径和曲率半径对管道最大应力的影响，结果如图9、图10和图11所示。由图9可知：管道的最大应力随中间直管长度的增大而增大。这是因为管道中间直管长度的增加导致管道模态频率下降，管道的模态频率接近基础振动频率，引起管道振动加剧。与X向和Y向振动相比，Z向振动下管道最大应力最小。由图10可知：管道最大应力随管道内径的增大而减小。这是因为管道的内径增大，使得管道的模态频率增大，导致管道的模态频率远离基础振动频率，Z向振动下管道的最大应力小于X和Y向振动下的管道最大应力。由图11可知：管道的最大应力随曲率半径的增大而增大，这是因为随着管道曲率半径的增加，管道的模态频率越来越低，导致管道的一阶模态频率接近基础振动频率。在曲率半径大于50 mm 后，当出口端曲率半径增加时，对应的管道最大应力明显大于进口端曲率半径增加时对应的管道最大应力，说明出口端曲率半径的变化对管道最大应力的影响比进口端的大。

图9 管道最大应力随中间直管端长度的变化Fig.9 Change of the maximum stress of the pipeline with the length of the middle straight pipe end

图10 管道最大应力随管道内径的变化Fig.10 Change of the maximum stress of pipeline with inner diameter of pipeline

图11 管道最大应力随曲率半径的变化Fig.11 Change of the maximum stress of pipeline with radius of curvature

4 空间管道出口压力波动分析

设定振动幅值为1 mm，振动频率变化范围为20~200 Hz，仿真分析不同振动方向下振动频率对管道出口压力波动幅值的影响，如图12所示。由图12可知：当基础振动频率接近管道模态频率时，管道出口压力波动幅值会增大；当20≤f＜100 Hz时，X向、Y向和Z向振动同时在基础振动频率f为80 Hz 时达到极大值，其中Y向振动下的管道出口压力波动幅值最大，X向振动下的管道出口压力波动幅值最小；当100≤f≤200 Hz，基础振动频率为160 Hz 时，管道出口压力波动幅值最大，这是因为此时基础振动频率接近管道二阶模态频率。

图12 出口压力波动幅值随振动频率变化的规律Fig.12 Change of outlet pressure fluctuation amplitude with vibration frequency

设定基础振动频率为60 Hz，分析基础振动幅值为0.5~1.5 mm 时管道在X向、Y向和Z向振动下出口压力波动幅值的变化，如图13所示。由图13可知：随着基础振动幅值增加，管道的出口压力波动幅值逐渐增大。由于双向流固耦合的作用，管道振动的加剧使得管道出口压力波动幅值呈现增加的现象。与Y向和Z向振动相比，X向振动下管道出口压力波动幅值最小。

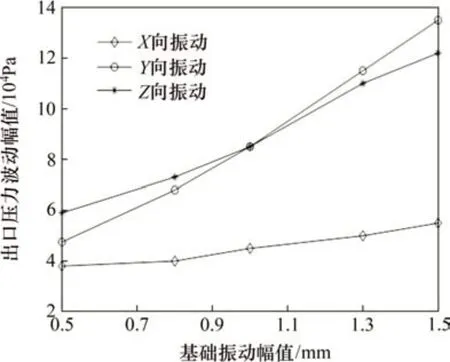
图13 出口压力波动幅值随振动幅值变化的规律Fig.13 Change of outlet pressure fluctuation amplitude with vibration amplitude

5 实验验证

实验系统原理如图14所示。实验系统由液压控制回路系统、振动系统、实验管道系统和数据采集系统4个部分组成。

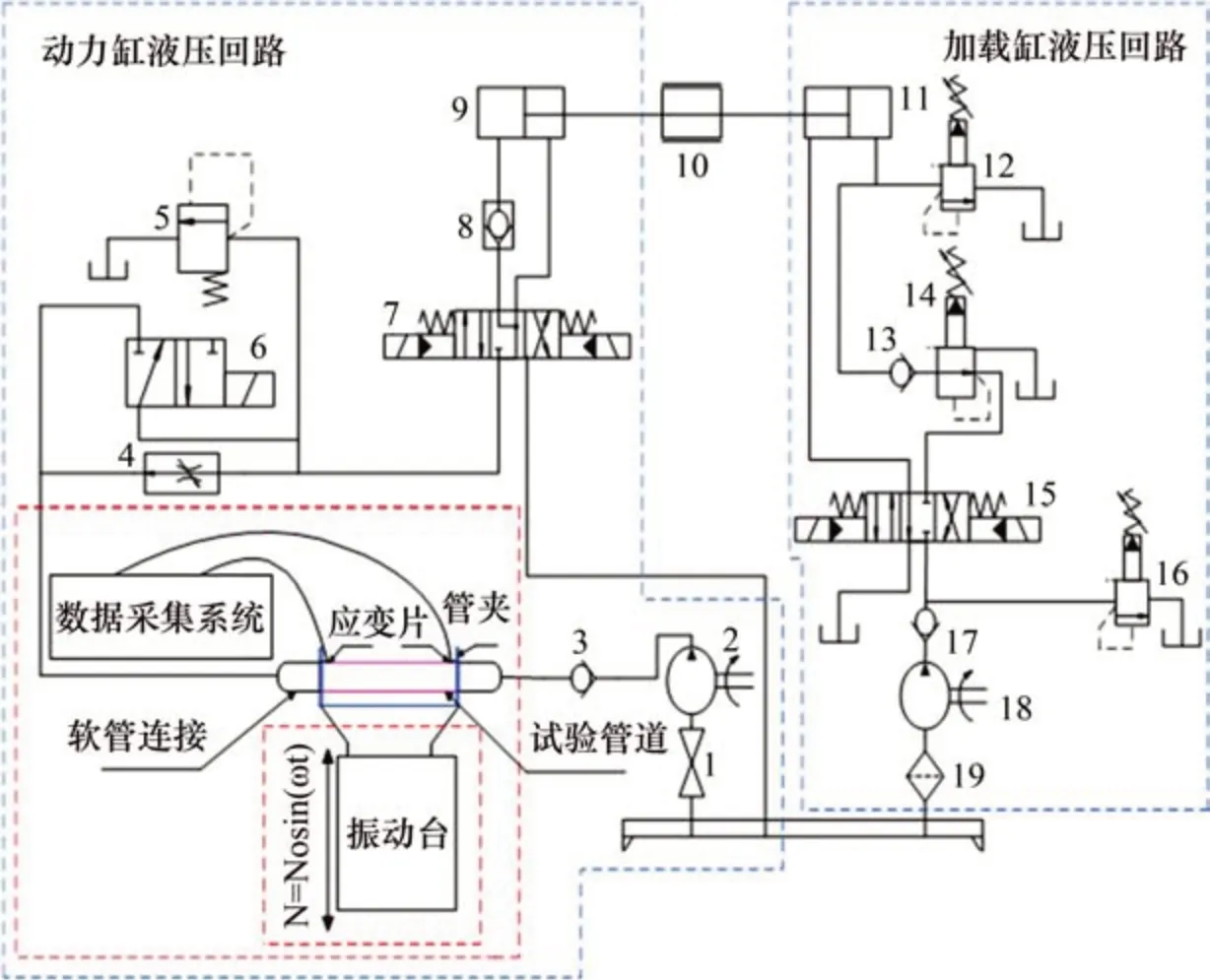
图14 实验系统原理图Fig.14 Schematic map of experimental system

设置完液压系统参数，启动振动台，设置采样频率为1 000 kHz，得到基础振动幅值为1.0 mm和基础振动频率为60 Hz时管道轴向应力的实测曲线，如图15所示。由图15可见：在数据采集时间为20~25 s，实验得到管道轴向应力波峰均值为5.62 MPa，波谷均值为-5.16 MPa。对同参数条件下管道应力进行仿真，并导出同节点应力，如图16所示。由图16可知：仿真得到的管道轴向应力曲线与实验得到的曲线形态大致一致，仿真得到轴向应力波峰均值约为6.44 MPa，波谷均值约为-5.54 MPa。与实验值相比，管道轴向最大应力仿真值与最小轴向应力仿真值的相对误差分别为14.59%与7.36%。

图15 实测应力结果Fig.15 Experimental stress results

图16 仿真应力结果Fig.16 Simulated stress results

设定基础振动频率为60 Hz，当基础振动幅值从0.4 mm增加到1.2 mm时，实验测得不同振动幅值下管道轴向应力最大值随基础振动幅值的变化规律，并与仿真值进行对比，如图17所示。由图17可知：随着基础振动幅值增加，管道轴向应力最大值实验值与仿真值有相同的变化趋势，实验值与仿真值最大相对误差为16.26%，平均相对误差为12.38%，均在合理的范围内，验证了仿真模型的正确性。

图17 不同振幅下管道轴向应力最大值实验结果与仿真结果对比Fig.17 Comparison of experimental and simulation results of the maxmium stress of pipeline at different vibration amplitudes

6 结论

1)建立了基础振动下空间管道双向流固耦合仿真模型，实验验证了仿真模型的正确性。

2)随着基础振动频率的增大，管道的最大应力和出口压力波动幅值均先增大后减小；当基础振动频率接近管道模态频率时，管道最大应力和出口压力波动幅值最大；随着基础振动幅值增大，管道最大应力和出口压力波动幅值逐渐增大。

3)随着管道曲率半径的增大，管道的最大应力逐渐增大，出口端曲率半径的变化对管道最大应力的影响比进口端的大，当出口端曲率半径为125 mm 时，管道最大应力是进口端管道最大应力的1.35倍。