基于主成分分析法的赤足迹预测身高模型
2020-05-21贺矗
贺 矗
利用足迹分析身高是足迹检验工作中非常重要的一部分,长期以来有大量的学者研究足迹与身高的关系。但是已有的研究并没有关注所测量的足迹不同部位之间是否具有相关性,当这些测量值之间存在高度相关性时,建立的回归模型会出现多重共线性问题,多重共线性可能会导致分析结果出现一些不合理的情况。本文选用主成分分析法和多元回归结合的方式通过赤足迹建立预测身高模型。
1 研究变量与分析
1.1 变量选取
研究对象是中国刑警学院在校学生和干训学员,实验对象没有足部疾病,在相同的实验环境下采用油墨捺印的方式让实验对象自然行走。共采集100 人的赤足迹。
结合当前已有的研究成果[1-4],以左足迹为例选取8 个变量进行主成分分析。分别是跖内缘到跟平行线(X1)、足长(X2)、跖宽(X3)、跟宽(X4)、第一趾前缘到跟(X5)、第五趾前缘到跟(X6)、第一趾前缘到跟平行线(X7)、第五趾前缘到跟平行线(X8),各变量如图1 所示。

图1 足迹测量示意图
1.2 数据分析
多重共线性分析。在进行多元回归分析时有个基本假设是各变量间相互独立,如果两个或多个变量之间出现了相关性,则称为多重共线性[5]。多重共线性会导致回归系数符号出现错误,即积极变量被认为是消极变量。用赤足迹的各个变量与身高建立回归模型时不仅要考虑各变量与身高的相关性,还要考虑各变量间的相关性。本文所采用的各变量与身高的相关性如表1 所示,各变量间的相关性如表2 所示。
以0.7 为阈值,可以从表1 中看出变量X2、X5、X6、X7、X8 都与身高具有相关性,假定不考虑多重共线性,直接建立多元回归公式如下。
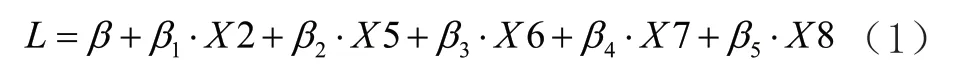
但是从表2 可以看出,变量X2、X5、X6、X7、X8 之间是具备相关性(浅灰色区域)的,甚至具备极强的相关性(深灰色区域)。本文采用主成分分析法提取出变量间的主成分,以新的主成分作为独立变量进行回归分析达到消除共线性问题。
2 主成分分析法
2.1 主成分分析法原理
主成分分析法(Principal Component Analysis,PCA)的核心思想是降维,将多组存在线性关系的变量通过正交变换的方法转换为几组线性不相关的变量,此时的变量即为主成分[5]。此方法能够克服单一变量不能准确预测身高的问题,实现更为科学准确的预测。

表1 变量与身高的相关性
2.2 实证分析
从100 人的实验数据中共选取了25 人的左赤足迹,并对数据进行标准化处理并得出相关系数矩阵,运用matlab 软件对系数矩阵进行主成分分析,各主成分得分如表3 所示,可以看出第一主成分(F1)主要包含跖内缘到跟平行线(X1)、第一趾前缘到跟(X5)、第一趾前缘到跟平行线(X7)。X1、X5、X7 都是足内侧的前端到后端的测量距离,可以将第一主成分解释为足内侧前后间的距离。第二主成分(F2)主要包含第一趾前缘到跟(X5),并且占很大比重,可以将第二主成分近似解释为第一趾前缘到跟(X5)。第三主成分主要包含跟宽(X4),可以将第三主成分近似解释为跟宽(X4)。第四主成分主要包含跖宽(X3),可以将第四主成分近似理解为跖宽(X4)。从表2 中可以看出降维后得到的4个主成分相关性非常弱,消除了多重共线性问题,可以对4 个主成分进行多元线性回归。
3 多元回归模型
由实验采集数据和主成分得分系数可以计算出主成分得分,利用matlab 对各主成分得分进行多元回归分析,获得多元线性函数如下。
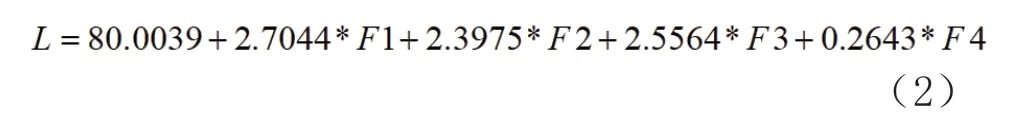
用公式(2)对25 组数据的身高进行预测,各预测身高和真实身高的最小相对误差绝对值是0.084%,最大相对误差绝对值是10.341%,平均相对误差绝对值是3.891%。25 组数据中有20 组数据的最小误差绝对值是小于6%的,说明利用公式(2)预测身高的精确度较高。同时对100 人的身高进行预测,在正负3 的误差范围内比当前已有的回归公式预测准确度高出7%至34%。

表2 各变量间的相关性

表3 主成分得分系数
4 结论
本文首先从正态分布的角度考虑了实验数据的价值,其次探讨了身高和8 个变量以及变量之间的相关性,然后运用主成分分析法对变量参数进行降维得到4 个主成分,最后利用主成分建立回归模型。
1)主成分分析法可以将众多与身高具有相关性的变量进行降维,消除多重共线性对回归模型的影响。
2)经过主成分分析后提取的4 个主成分包含了原始样本数据95%以上的信息,能够充分保障回归模型的准确性。
3)主成分回归模型平均相对误差绝对值是3.891%,表明主成分分析后再进行多元回归获得的模型精度较高,在正负3 的误差范围内比当前已有的回归公式预测准确度高出7%至34%。
