多航天器协同探测效能影响参数不确定性分析

高 辰，杨 震，张玉珠，牛文龙

(1. 中国科学院国家空间科学中心，北京 100190；2. 中国科学院大学，北京 100049)

0 引 言

航天任务的设计是一项多学科融合的复杂过程[1- 2]。一个空间科学任务的概念设计阶段是工程师把科学家的科学目标工程化论证的过程。通常一个空间任务系统在总体设计阶段投入的人力和资源只占整个任务的10%，却决定了任务系统80%的生命周期成本[3]。而在设计过程中，存在大量的不确定性因素[4-5]，这些不确定性因素既包括由于认知的局限性导致的认知不确定性，也有尺寸、测量等精度导致的参数误差引起的随机不确定性。认知不确定性通常通过非概率数学的方法解决。针对随机不确定性，根据研究对象的不同分为灵敏度分析和不确定性分析[6]。其中，灵敏度分析研究的是某一参数变化时，系统整体性能的改变程度。而不确定性分析研究的是在每一参数都具有不确定性的情况下，系统整体性能的不确定性的大小。航天任务概念设计阶段，考虑不确定性在多学科复杂系统的优化设计中的影响有助于建立多学科优化特性和性能评价，有着重要的意义[7]。在设计初期进行参数的不确定性分析可以评估在当前的设计下，能否满足对科学目标的探测；以分析不同参数对于探测性能影响程度；进而对参数设计进行优化。

随着航天科技的进步，分布式卫星系统的应用越来越广阔。在空间科学任务中，分布式卫星系统可以观测到以前难以探测的物理现象和天文数据，使空间探测进一步发展。如欧空局2000年发射的Cluster II任务[8]。NASA在2015年3月发射的对MMS(Magnetospheric Multiscale)任务[9]。JAXA计划发射的SCOPE任务[10]。国内刘振兴院士团队提出的“磁层-电离层-热层耦合探测计划”(Magnetospher-Ionosphere-Thermosphere, MIT)[11]。而随着分布式卫星系统在空间科学任务中越来越广泛的应用，系统中更复杂的参数耦合关系对不确定性分析提出了更高的要求和挑战。在Cluster II和MMS任务中，不确定性参数的分析工作主要集中在建立分布式卫星系统构型或其他实际工程参数的评价方法[12]。目前，在分布式卫星系统概念设计阶段，对系统探测效能的不去额定性分析的研究较少。通常都是利用概率统计和数值模拟的蒙特卡洛方法解决。

航天任务概念设计阶段不确定性分析具有涉及学科多、系统函数表征难、参数描述粗略和不同任务间独特性强的特点[13]，航天任务的不确定性分析主要针对单一学科[14-15]，整体考虑较少。基于不确定性多学科优化设计的卫星总体设计方法可以提高卫星总体设计质量[16]。且因为概念设计阶段是一个需要迭代设计的过程，减少分析工作的时间具有重要的意义。因此，不确定性分析的需求主要可归结为以下四个方面：计算效率高，定性分析为主，普适性强，能够对未知的参数耦合关系进行识别分析。

针对传统基于蒙特卡洛仿真的探测效能评价方法中时间效率低，参数关系映射单一的问题，本文提出一种基于神经网络的不确定性分析方法，利用人工神经网络在拟合回归分析上的非线性特性，设计了能够替代复杂系统的神经网络结构，在网络训练阶段，与蒙特卡洛方法相比，能够通过少量仿真计算结果作为训练样本实现模型的收敛。在参数不确定性分析时，有效反映被替代系统的原有特性。从而避免了基于仿真采样方法计算量大的问题。并以一个多航天器的天文观测任务为背景，进行了仿真实验，并对实验结果进行了分析对比。实验结果证明本文方法在具有更高计算效率的同时具有较高的准确性。

1 科学卫星任务设计中的不确定性描述

执行空间科学任务的卫星，其工作过程看作在沿着轨道运动的过程中，记录下每个测量点位置姿态P，时间t，有效载荷的测量值V及其他参数。以单一卫星的探测过程为例，如所图1所示，卫星在t1,t2,t3时刻分别记录下卫星所在的位姿P1,P2,P3，有效载荷探测结果V1,V2,V3。对于一个空间科学任务，尤其是对于分布式卫星系统，其工作过程就是通过对这些时序变量的测量，并结合合适的计算方法，实现对复杂物理现象的探测。

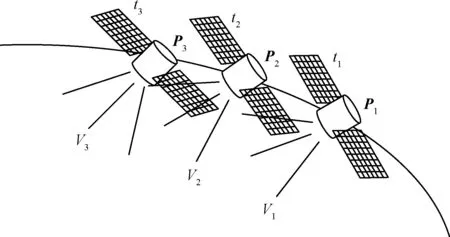
图1 卫星探测过程Fig.1 A satellite detection process

但是，在卫星的实际运行过程中，因为不确定性的普遍存在，卫星的定位定姿，时钟系统，有效载荷都不可避免的存在测量的不确定性。如图2所示，图中灰色卫星的真实状态为，在t1,t2,t3时刻，卫星的探测测量值对应的为t′1,t′2,t′3，P′1,P′2,P′3和V′1,V′2,V′3。在任一时刻，每次的测量值误差都不相同，在卫星的系统设计中，通常通过位姿测量精度uP，时钟精度ut，有效载荷测量精度uV等来描述其统计规律。

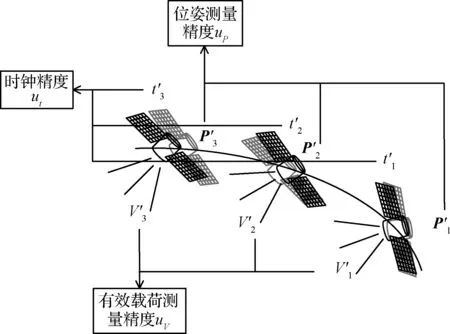
图2 不确定性参数影响下的卫星探测过程Fig.2 A satellite detection process with uncertainty

在传统的卫星系统分析中，大部分的误差、灵敏度分析针对的都是在某一时刻t，参数的具体误差，如有效载荷的测量误差ΔV=V′-V，时钟误差Δt=t′-t，位姿误差ΔP=P′-P等，会对系统产生多大的影响。而对于连续探测过程中，引起这些误差的不确定性参数uV，ut，uP的分析较少。如而对于大部分执行空间科学任务的分布式卫星系统，因为其探测过程本身是一个基于时间的连续过程，考虑这些不确定性参数对于系统的影响对于卫星系统早期的设计工作有着重要的意义。

单一卫星的探测过程可以通过下式进行描述。

(1)

式中:y为卫星系统最终的探测目标，其通过系统函数g()求解。g()的参数为卫星系统探测过程中的时序测量结果，如时间信息序列T，卫星位姿信息序列P，有效载荷测量值序列V。因为在实际工程中，误差的普遍存在，在任意时刻，这些测量值相对于真值始终存在一定偏差。即t′i=ft(ti)，P′i=fP(Pi)，V′i=fV(Vi)等[17]。根据这些误差产生的原因不同，可以确定其对应的概率分布。在航天任务的概念设计阶段，对参数的不确定性的描述通常是通过标量进行粗略设计说明。如定位精度50 m，时钟精度20 ns等。在实际工程中，对于未指定分布形式的不确定性参数，常用做法是使用高斯分布进行描述[18]。在此基础上，参数描述如下：

(2)

在探测过程中，当这些误差存在时，系统对探测目标的探测结果y也与理想值yr存在误差：Δy=y-yr。如何评估在这些不确定性参数影响下，尤其是在空间多点探测任务中，Δy的变化规律，是研究重点。

2 航天任务的不确定性分析过程

2.1 应用背景介绍

在空间分布式多点探测任务中，每一个航天器都是一个独立的探测系统，而整个任务的科学目标能否达成，需要充分利用每个探测系统的测量值。随着不确定性参数的增多，整个系统的不确定性分析也变得更加复杂。以一个多航天器的天文观测任务为例，其任务系统由一个主卫星和八个子卫星组成，运行轨道为理想的近月轨道。每两个航天器可构成一条观测基线，随着轨道进动，实现对全天区的三维观测[19]。

在此任务中，被测目标为宇宙背景辐射，其成像原理与综合孔径微波辐射计类似。其简化的成像原理如下式：

V(u,v)exp(2πj(uξ+vη))

(3)

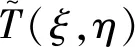
2.2 任务仿真流程设计

考虑了不确定性参数之后的仿真流程如图3所示。

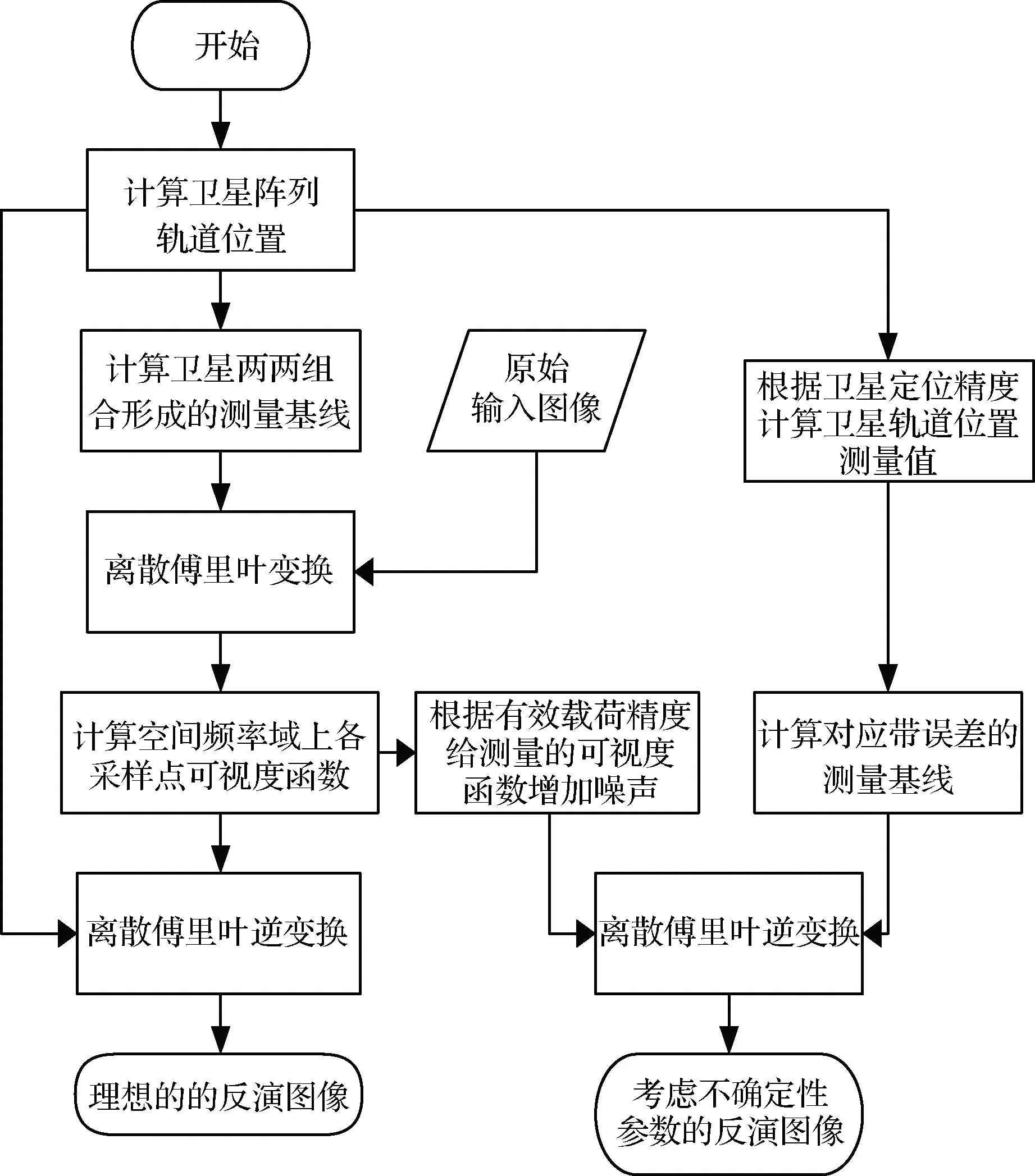
图3 考虑不确定性参数的仿真流程Fig.3 Flow chart of the simulation process with uncertainty

如前文所述，考虑的任务的不确定性参数主要为卫星轨道的定位误差，有效载荷精度引起的测量可视度函数的幅值和相位误差。在正常的仿真流程之外，根据卫星的定位精度，在卫星的探测过程中，每次生成带误差的定位结果，进而计算出，空间频域带误差的测量基线位置(u′,v′)；再根据有效载荷的精度，对应的给测量到的可视度函数增加噪声，得到可视度函数的测量结果V′(u,v)。根据新的测量基线(u′,v′)及其对应的可视度函数V′(u,v)，计算考虑不确定性参数的反演图像T′。

在传统的综合孔径微波辐射计的成像误差分析中，最常用的定量评估指标是均方根差[20-22]，通过计算含误差项的反演结果与理想反演结果之间的各像素点的均方差来衡量反演结果的误差大小。

其中，对于两张尺寸同为尺寸的图像，其均方根差(Root Mean Square Error)的计算方程如下:

(4)

式中:m和n分别为图像的宽和高，Te(ξ,η)为考虑误差的成像结果，Ti(ξ,η)为不考虑误差情况下的理想成像结果。这种评价探测反演结果的好处是均方根差不仅体现了Te(x,y)和Ti(x,y)之间的平均偏差，也包含了随机噪声偏差[23]。

3 不确定性分析方法

3.1 传统蒙特卡洛仿真的分析方法

蒙特卡洛方法是广泛应用的一种计算算法，它的计算过程依赖于重复随机采样来获取数值结果。其基本思想是通过使用随机性来解决确定性问题[24]。

设一个系统的函数描述为：

y=g(x1,x2,…,xn)

(5)

式中:x1,x2,…,xn为这个系统的n维输入变量，y为系统的输出。考虑系统输入变量具有的随机不确定性条件下，利用蒙特卡洛抽样仿真方法进行系统不确定性分析的方法如下：

1) 根据n维输入变量x1,x2,…,xn的联合概率分布，生成M个样本：

(6)

2) 计算对应的M个系统响应输出为：

y=[y1,y2, …,yM]T

(7)

3) 对结果的方差进行统计分析，得到系统的无条件方差D：

(8)

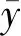
蒙特卡洛等概率抽样方法，其本质是通过大量随机实验，利用概率论解决问题的一种数值方法。在不确定性分析中，从其计算流程可以看出，蒙特卡洛方法需要在确定参数的不确定性的前提下，通过大量仿真计算，得到多次抽样结果，再利用统计的方法，给出不确定性分析结果。其计算精度与仿真重复计算次数成正比。根据大数定律当采样计算次数足够充分时，基于概率统计的蒙特卡洛仿真方法的计算结果被认为最接近真实情况。因此通常选为作为对比的基本方法。而在航天任务的早期设计阶段，不确定性参数往往是需要优化设计的指标，每一组参数条件都进行蒙特卡洛仿真计算时间成本高。同时，蒙特卡洛方法不能给出参数之间耦合关系的变化规律，不利于航天任务在早期阶段进一步优化设计。

3.2 神经网络模型替代的分析方法

本文引入人工神经网络模型的方法，通过在参数可行空间能进行少量采样计算的方法作为训练样本，对神经网络进行训练，用训练后的神经网络作为复杂系统的替代模型，改善单独使用蒙特卡洛方法在航天任务早期设计阶段的不足。其计算流程如图4所示。

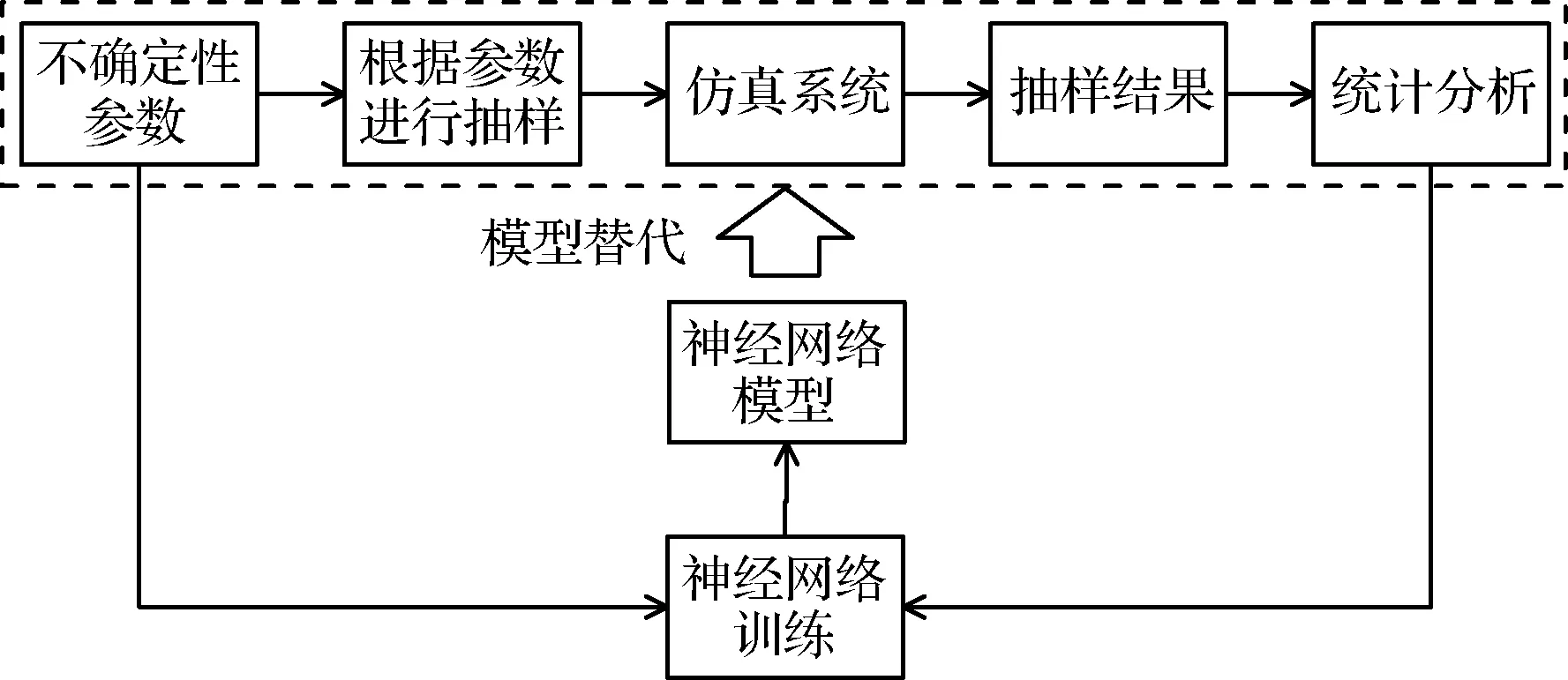
图4 神经网络模型替代的分析方法流程Fig.4 Process of neural network model method

4 仿真校验

4.1 基本仿真参数配置

为了减少反演算法对结果的影响，在仿真中依然采用还原质量一般的基本线性直接离散二维傅里叶逆变换求解反演图像[25]。输入图像为一张32×32的灰度图，在图像中间左侧位置有一矩形明亮区域，赋值为1，其余区域的幅值为0。在不考虑任何输入不确定性参数的情况下，输入原始图像和对应算法的反演图像如图5所示，其中，左侧为输入的原始图像，右侧为不考虑不确定性参数情况下的反演结果。

因本文的重点不是对反演算法产生的误差进行评估，固不对反演算法问题做深入探讨。

4.2 蒙特卡洛仿真分析结果

为分析系统在不同参数不确定性条件下的整体性能不确定性，基于前文中描述的考虑不确定性参数的仿真环境，利用蒙特卡洛方法对系统进行抽样仿真分析的参数精度如表1所示。

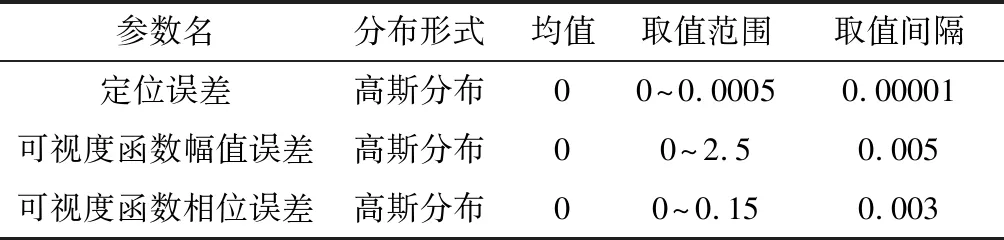
表1 蒙特卡洛仿真参数Table 1 Parameters in Monte Carlo Simulation

其中，卫星的定位误差使用误差椭球模型[26]，即在卫星的每一次定位过程中，三维误差的分布呈椭球状。在卫星位置误差分析的模型中，通常假设定位误差在三个方向均服从相同的高斯分布，即误差椭球退化为误差球，误差球半径为设定的标准差。在综合孔径微波辐射成像仿真中，通过在可视度函数的幅值和相位分别增加高斯噪声来模拟环境和硬件引起的可视度函数误差。因研究重点讨论的是不确定性参数的分析方法，为减少实际工程参数选择的影响，单位均使用无量纲，且参数的数值范围保证对最终结果的影响在同一数量级。经实验，可视度函数相位不确定性在0.1时，在不考虑其他参数的不确定性，系统整体的探测效能的不确定性为0.0068；而可视度幅值误差不确定性在2.4时，在不考虑其他参数的不确定性，系统整体的探测效能的不确定性为0.0063；而定位精度不确定性在0.00034时，在不考虑其他参数的不确定性，系统整体的探测效能的不确定性为0.0068。基于此，卫星定位精度参数的标准差为0～0.0005，可视度函数的幅值误差范围在0～0.25范围内，可视度函数的相位误差在0～0.15范围内。在具体抽样方法中，对各维参数空间均匀采样50次，即在定位精度的标准差采样取值间隔为0.00001，可视度函数的幅值误差的标准差采样间隔为0.005，可视度函数的相位误差的标准差采样间隔为0.03，共在参数空间采样50×50×50=125000个采样点。在每组参数条件下，再利用蒙特卡洛抽样计算500次，并对结果求平均值，作为在这组输入不确定性参数条件下，系统整体效能不确定性的评价指标。蒙特卡洛的部分仿真结果如图6所示，其中，图6(a)在考虑了参数耦合关系后的不确定性参数与结果的变化趋势。图6(b)为两种参数误差的二维示意图，系统整体效能蓝色代表不确定性误差为0，黄色代表不确定性误差增大至约0.012。从中可以看出，两个参数之间存在耦合关系，并非独立的不确定性参数。利用蒙特卡洛仿真的方法计算量大，耗时长，在当前参数组合下，需要重复计算62500000次，且当参数再次变化时，需要再次进行计算。

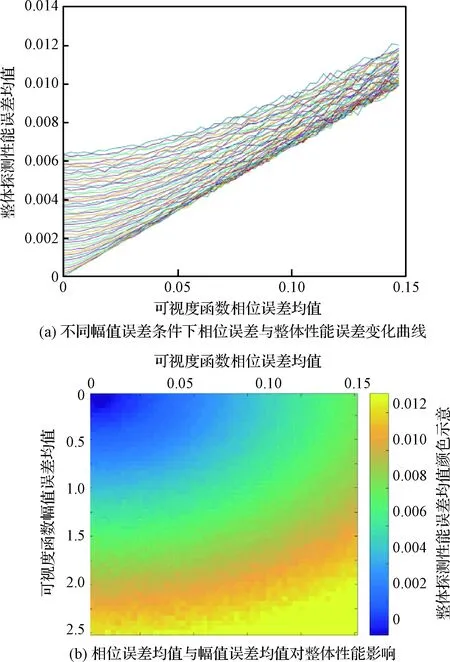
图6 可视度函数幅值误差均值不同时相位误差 均值与整体性能误差均值的变化规律Fig.6 Result from MCS of two coupling parameters

4.3 神经网络替代模型方法实验结果

为减少重复计算次数，提高系统在设计阶段的设计效率，本文引入人工神经网络作为系统模型替代的方法进行不确定性分析。

在上节蒙特卡洛方的基础上，以可视度函数幅值误差和可视度函数相位误差作为分析参数。利用Matlab软件的神经网络工具包，构建一四层BP神经网络作为替代模型，神经网络中有2个隐含层，每一个隐含层有3个节点，第一个隐含层的激活函数为tansig函数。考虑到误差的描述恒为正值，第二个隐含层激活函数选择logsig函数，logsig函数为对标准sigmoid函数求对数，可以将(-∞,+∞)的输入值，映射到[0，1]范围内。输出层同样选择简单线性函数purelin。具体网络结构如图7所示。

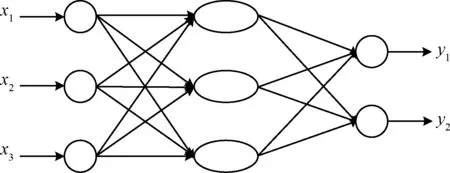
图7 神经网络结构示意图Fig.7 Structural of neural network model

在进行不确定性分析时，因为不确定性的数值相对较小，为减少对训练过程的影响，需要对数据进行归一化处理，其归一化处理的方法如下：

(9)

在训练样本选择时，训练样本数量对训练结果影响如表2所示，可以看出，随着样本数量的增加，对系统的拟合程度也更精确，使神经网络模型可以更有效逼近原有系统特性。

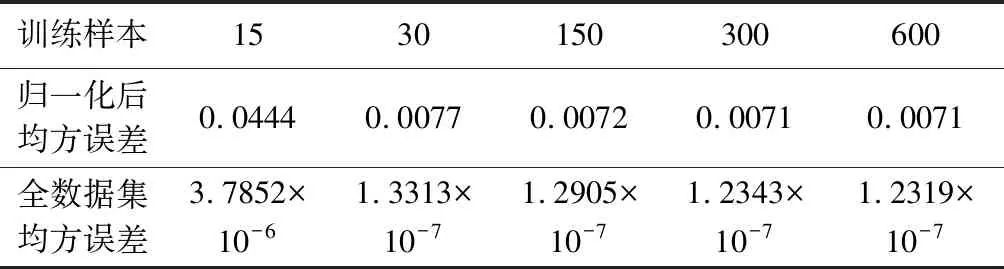
表2 训练样本数量对训练结果影响Table 2 Mean Square Error of different training samples

在考虑训练稳定性和收敛速率后，本文使用的训练样本为上节中蒙特卡洛仿真结果的1/4，即将可视度函数幅值误差和相位误差的取值间隔增大一倍，训练样本大小为25×25共625个。经过106次迭代训练后，与蒙特卡洛50×50的结果对比如图8和图9所示。其中，图8中‘*’构成的曲线为蒙特卡洛仿真结果，‘o’构成的曲线为神经网络模型替代方法的结果；图9为神经网络模型替代方法结果的二维示意。

在数据归一化后，2500个实验样本的均方误差约为0.007，在原有数值区间均方误差约为1.23×10-7。可以看出，神经网络模型替代方法相对于蒙特卡洛仿真的结果差距不大。而在当前实验条件下，蒙特卡洛仿真计算一组参数的计算时间约为2 min，计算2500个样本的时间约为1.5 h。神经网络模型替代方法的训练样本生成仅需原蒙特卡洛方法的1/4时间。训练过程约5 min，后续计算其余时间可忽略。可见整体计算时间效率提升明显。

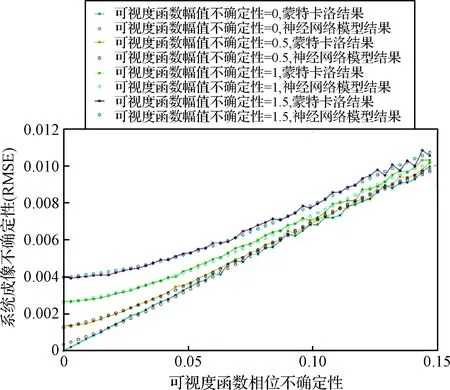
图8 神经网络模型替代法结果与蒙特卡洛结果对比Fig.8 Result comparison of Monte Carlo Method and ANN method

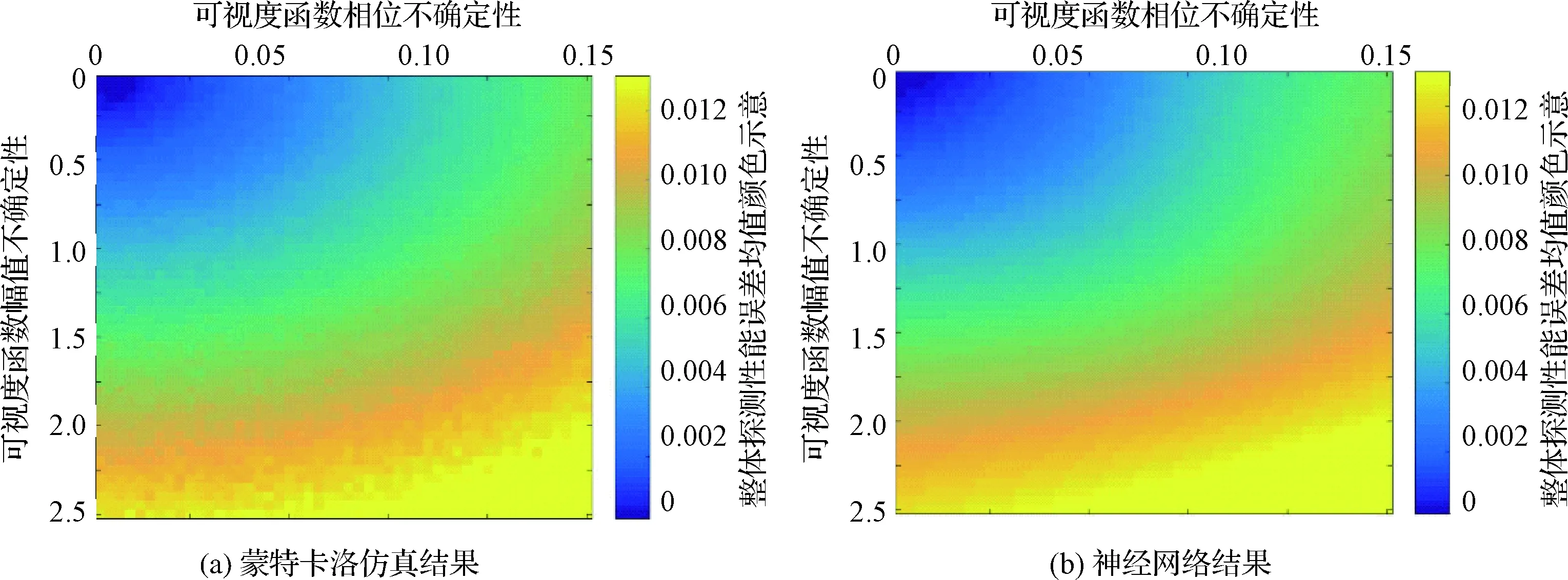
图9 神经网络模型替代法结果与蒙特卡洛结果对比Fig.9 Comparison between neural network model and MCS

5 结 论

不确定性分析是航天任务尤其是空间科学任务在早期设计阶段的重要组成部分。参数的不确定性会影响任务的科学目标能否满足，是评价系统整体效能的重要依据。随着航天器数目的增加，空间多航天器协同探测任务的不确定性分析复杂度越来越复杂。蒙特卡洛仿真分析方法是解决这一难题的主要手段，但其也有时间效率低，不能对参数之间耦合关系进行有效识别等弊端。

本文利用人工神经网络在拟合回归分析上的非线性特性，提出一种基于神经网络的不确定性分析方法，设计了能够替代复杂系统的神经网络结构，在网络训练阶段，与蒙特卡洛方法相比，能够通过少量仿真计算结果作为训练样本实现模型的收敛。在参数不确定性分析时，有效反映被替代系统的原有特性。避免了大量重复计算。仿真验证以天文多星观测成像为背景，通过与蒙特卡洛方法的结果对比，证明了方法的有效性。为实际多星任务在早期任务设计阶段的不确定性分析提供新的解决方案。