基于Matlab GUI的股票价格走势模拟系统开发

赵步祥　杨德平

摘要：为开发一个供股票从业者和研究人员使用的股票预测工具，本文对基于Matlab GUI的股票价格走势模拟系统进行开发。通过对股票市场的特点、预测模型的种类及相关变量等方面的调研，选取随机游走模型、一般化的维纳过程模型、几何布朗运动模型及含跳跃影响模型来模拟股票价格走势，开发了具有功能的Matlab GUI系统，用作股票分析的工具。研究结果表明，随机游动模型价格具有不确定性，而对于几何布朗运动和含跳跃维纳过程，虽然单次模拟价格具有随机性，但多次模拟具有一定程度的确定性。开发的界面操作简单，避免了繁琐的建模计算过程，方便股票市场参与者使用。该研究具有一定的应用前景。

关键词：随机游走; 维纳过程; 几何布朗运动; 跳跃影响; 图形用户界面

中图分类号： F830.91; TP317.4文献标识码： A

文章编号： 1006-9798（2020）02-0116-09; DOI： 10.13306/j.1006-9798.2020.02.018

股票价格是由市场的每个参与者共同决定，但由于各个参与者行为的不可预测性，一般认为股票市场是混沌的，股票价格难以预测，且其价格还受到经济等其他因素的影响，包括货币供给与需求、失业率、通胀及经济周期等。针对股票价格波动的特点，合理准确的预测股市股票价格的变化趋势成为许多学者主要研究的方向。关淞瀚[1]通过归纳发达国家股票市场的特点，认为发达国家的股票更好预测;李缃珍[2]认为短期的股票市场趋势预测对政府管理证券市场有重要意义;刘平等人[3]认为股票市场的不稳定来源于价格波动的非线性和时变性等特点;陈婕[4]认为股票投资者买卖的依据是自己的预期，但投资者的决策还受许多其他非理性因素的影响，这降低了预测模型的准确性;王春峰等人[5]认为所有预测模型的前提是未来金融市场波动模式与过去相同，即市场风险测量的核心是对过去收益率波动性的估计;杨克磊等人[6]比较了深圳股市和上海股市的波动特点，认为上海股市风险较高;杨光艺[7]认为预测模型的预测变量在熊市和牛市中有不同的意义。关于预测模型的研究，刘光强[8]建立了中国股市的高频波动预测模型，发现自回归搜索（autoregressive quest，ARQ）模型和异质自回归搜索（heterogeneous autoregressive quest，HARQ）模型有很高的准确度;姜富伟[9]发现中国的投资组合具有显著的样本外和样本内可预测性;张斌[10]认为数据的波动类型会影响模型的准确性;沈巍[11]认为现阶段的预测模型存在无法加入非量化因素等问题;蒋志强等人[12]认为中国股市收益率是可预测的，但是各投资组合的可预测性在不同股市状态下存在差异等;周孝华[13]在股票运动混沌性假设的基础上，分析布朗运动与分形布朗运动的仿真过程，首次提出并论述了分形布朗运动是股价行为的高度逼真;郭精军[14]用分式布朗运动模拟上证指数，得到了很好的预测精度;张永东[15]使用指数平滑模型对上海股市的股票进行预测，预测结果优于其他模型;谢琪等人[16-18]采用神经网络模型对股票价格进行预测;卢嘉澍等人[19-20]采用马尔科夫链预测模型对股票价格进行模拟。近年来，图形用户界面（graphical user interface，GUI）受到了股票参与者的青睐，它可以根据股票特点调整参数，设计出针对性强的股票分析预测界面，杨晓等人[21]基于Matlab GUI，开发了马氏链股价预测系统用于经济领域。因此，本文在总结了股票预测模型研究现状的基础上，对基于Matlab GUI的股票价格走势模拟系统进行开发，设计了一个提供几种预测模型的GUI界面，用作股票分析的工具。该设计组合界面操作简单友好，避免了繁琐的建模计算过程。该研究对股票市场参与者具有重要的应用价值。

1模型理论

1.1对数收益率模型

多期股票对数收益率为

1.2随机游走模型

价格随机模型的基本形式为

式中，μ为股票的年预期收益率;σ为股票价格年波动率。

1.3一般化的维纳过程模型

一般化维纳过程的基本形式为

式中，ΔS表示股票价格S在很小的时间间隔Δt中的变化。若初始时刻t=0，股票价格为S0，则t时刻的价格St可表示为

1.4几何布朗运动模型

当研究不支付股息的股票时，其价格的变化特征可表示为

由于dW为维纳过程中不可预测项，且（dW）2=ε2dt，ε～N（0，1）。t时刻价格St的离散模型可表示为

1.5含跳跃影响模型

在研究含有跳跃因素影响股票时，其价格的变化特征可表示为

式中，k为t时段跳跃次数;Ni（t）为St的第i个跳跃触发St在t时刻发生跳跃的计数过程，是服从参数为λit的泊松过程，即

Ui是在时间间隔为hi，方差为σ2i上的随机跳跃幅度，其满足

设T为观察周期长度，按等时间间隔观察n次，即h=T/n，则第i次的价格表示为Sih（i=1，2，…，n）。當时间间隔h足够小时，这样能保证每一个间隔内至多发生一次跳跃，此时模型的离散形式为

其中，I|Nih-N（i-1）h=1|为示性函数，表示在第i时段上发生跳跃时取值为1，否则取值为0。

2界面开发

2.1界面组成与布局

本界面主要利用对数收益率模拟价格法，随机游走、布朗运动等方法模拟股票价格走势，包含输入数据、模型触控按钮和显示模拟图等控件，股票价格走势模拟功能界面如图所1示。

2.2控件属性设计

本界面由10个静态文本框、2个面板、6个按钮、8个可编辑文本框和2个坐标轴组成。控件属性设计如表1所示。

2.3程序设计

1）[对数收益率模拟价格法]按钮回调函数。

function duishushouyilvfa_Callback（hObject，eventdata，handles）

globalPrice0musigmaMN

Price0=str2num（get（handles.chushijiage，'string'））;%初始价格

N=str2num（get（handles.monitianshu，'string'））; %模拟交易日天数

mu=str2num（get（handles.yuqishouyilv，'string'））; %预期收益率

sigma=str2num（get（handles.yuqibodonglv，'string'））;%预期波动率

M=str2num（get（handles.monicishu，'string'））;%模拟次数

n=240;%假设一年有240个交易日

MU=（1+mu）^（1/n）-1;%年收益率转换成日收益率

SIGMA=sigma/sqrt（n） ;%年波动率转换成日波动率（近似）

PRICE=[]; %存储价格模拟值

for j=1：M

Rate=normrnd（MU，SIGMA，N，1） ; %随机产生N个正态分布随机数

S=Price0*exp（cumsum（Rate）） ;%计算各交易日的价格

PRICE=[PRICE，S];

end

Pmean=mean（PRICE，2）;

axes（handles.axes1）;

cla（handles.axes1）%清除坐标轴信息

x=1：N;

plot（x，PRICE（：，1））%绘制一次模拟价格走势

xlabel（'时间'） ;ylabel（'价格'）;

axes（handles.axes2）;

cla（handles.axes2） %清除坐标轴信息

plot（x，Pmean） %绘制模拟价格整体走势图

xlabel（'时间'）;ylabel（'均值价格'）;

guidata（hObject， handles）;

其它主要按钮的回调函数主要代码如下：

2）[随机游走运动]按钮回调函数。

function suijiyouzou_Callback（hObject，eventdata， handles）

global Price0musigmaMN

PRICE=[];%存放价格模拟值

for j=1：M

e=normrnd（0，1，N，1）;%隨机产生N个正态分布随机数

S（1）=Price0+e（1）;

for i=2：N

S（i）=S（i-1）+e（i）;%计算各交易日的价格

end

PRICE=[PRICE;S];

end

3）[几何布朗运动]按钮回调函数。

function jihebulang_Callback（hObject，eventdata， handles）

globalPrice0musigmaMN

T=1;%设时间周期长度为1

h=T./N;%时间间隔长度

PRICE=[]; %存放价格模拟值

for j=1：M

e=normrnd（0，1，N，1）; %随机产生N个正态分布随机数

S（1）=Price0*exp（mu*h+sigma*sqrt（h）*e（1））;

for i=2：N

S（i）=S（i-1）*exp（mu*h+sigma*sqrt（h）*e（i））; %计算各时刻的价格

end

PRICE=[PRICE;S];

end

4）[一般化维纳过程]按钮回调函数。

function yibanhuaweina_Callback（hObject，eventdata，handles）

globalPrice0musigmaMN

T=1; h=T./N;PRICE=[];

for j=1：M

e=normrnd（0，1，N，1）; %随机产生N个正态分布随机数

S（1）=Price0+mu*h+sigma*sqrt（h）*e（1）;

for i=2：N

S（i）=S（i-1）+mu*h+sigma*sqrt（h）*e（i）; %计算各时刻的价格

end

PRICE=[PRICE;S];

end

5）[含跳跃维纳过程]按钮回调函数。

function hantiaoyueweina_Callback（hObject，eventdata， handles）

global Price0musigmaMN

SIGMA=str2num（get（handles.tiaoyuebodonglv，'string'））;%跳跃波动率

p=str2num（get（handles.tiaoyuegailv，'string'））; %跳跃概率

Lambda=str2num（get（handles.tiaoyuefudu，'string'））;%跳跃幅度

T=1;h=T./N;PRICE=[];

for j=1：M

%产生每个时间段上维纳过程随机数

e=normrnd（0，1，N，1）;%利用参数为1的二项分布随机数取得示性函数

I=binornd（1，p，N，1）;%产生每个时间段上跳跃事件发生的幅度并计算价格

V=normrnd（log（1+h）-SIGMA^2/2，SIGMA^2，N，1）;

U=exp（V）-1;

S（1）=Price0+Price0*（（mu-（Lambda*h）*I（1））*h+sigma*sqrt（h）*e（1）+U（1）*I（1））;

for i=2：N

S（i）=S（i-1）*（1+（（mu-（Lambda*h）*I（i））*h+sigma*sqrt（h）*e（i）+U（i）.*I（i）））;

end

PRICE=[PRICE;S];

end

3系统应用

1）随机游走运动模拟只需初始价格、模拟天数和模拟次数3个输入量，随机游走运动模拟如图2所示。

2）几何布朗运动、一般化维纳过程、对数收益率模拟价格法需要初始价格、模拟天数、模拟次数、预期收益率和预期波动率5个输入量，几何布朗运动模拟如图3所示。

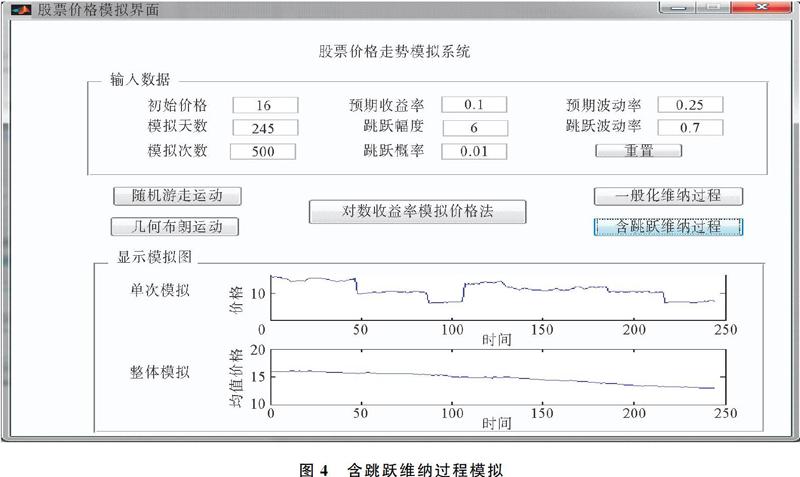
3）含跳跃维纳过程模拟需要界面全部输入量，含跳跃维纳过程模拟如图4所示。

由图2～图4可以看出，只要给出模型的输入变量，系统界面就会方便快捷地呈现出股票价格走势的模拟结果。从单次模拟和多次模拟平均结果可以看出，随机游走模拟价格都具有一定的波动性，说明随机游动模型模拟结果具有不确定性;而几何布朗运动和含跳跃维纳过程的模拟结果，虽单次模拟价格具有随机性，但从多次模拟平均结果来看具有一定的确定性。

4结束语

本文对基于Matlab GUI的股票价格走势模拟系统进行开发，设计了一个用作股票分析的GUI界面。试验结果表明，不同的预测模型模拟的结果具有不同的确定性。由于股票波动的混沌性，准确预测股票信息非常困难，但是本设计依然能给股票从业者提供参考价值。本文的不足之处是未对不同模型的适用条件进行详细划分，给理论基础不足的从业者带来不便，但是本设计依然具有应用价值。

参考文献：

[1]关淞瀚. 浅析股票市场的可预测性[J]. 中国商论， 2018（26）： 28-29.

[2]李缃珍. 股票市场短期趋势的离散分类预测模型研究[J]. 经济研究导刊， 2019（26）： 136-140.

[3]刘平， 于重重， 苏维均， 等. 股票价格市场波动优化预测仿真研究[J]. 计算机仿真， 2018， 35（8）： 179-183.

[4]陳婕. 技术分析有效性的实证研究[J]. 现代商业， 2014 （30）： 201-201， 202.

[5]王春峰， 张庆翠. 中国股市波动性过程中的长期记忆性实证研究[J]. 系统工程， 2004， 22（1）： 78-83.

[6]杨克磊， 毛明来， 徐正国. 随机波动模型的沪深股市比较研究[J]. 天津大学学报： 社会科学版， 2004， 6（4）： 334-338.

[7]杨光艺. 中国股市可预测性的稳健性检验[J]. 金融发展研究， 2018（12）： 3-9.

[8]刘光强. 我国股票市场高频波动预测研究——基于ARQ及HARQ模型的实证分析[J]. 西南交通大学学报： 社会科学版， 2017， 18（4）： 82-87.

[9]姜富伟， 徐俊， David E. Rapach， 等. 中国股票市场可预测性的实证研究[J]. 金融研究， 2011（9）： 107-121.

[10]张斌. 基于回声状态网络的短期股价预测模型[J]. 计算机应用与软件， 2017， 34（5）： 268-272， 333.

[11]沈巍. 股票价格预测模型研究[J]. 财经问题研究， 2009（7）： 89-93.

[12]蒋志强， 田婧雯， 周炜星. 中国股票市场收益率的可预测性研究[J]. 管理科学学报， 2019， 22（4）： 92-109.

[13]周孝华. 一种股票价格行为模式的一般化——从布朗运动到分形布朗运动[J]. 桂林电子工业学院学报， 2000， 20（4）： 95-99.

[14]郭精军， 田婧. 分式布朗运动模型下的金融市场风险度量——以上证指数为例[J]. 兰州商学院学报， 2014， 30（2）： 89-94.

[15]张永东， 毕秋香. 上海股市波动性预测模型的实证比较[J]. 管理工程学报， 2003， 17（2）： 16-19.

[16]谢琪， 程耕国， 徐旭. 基于神经网络集成学习股票预测模型的研究[J]. 计算机工程与应用， 2019， 55（8）： 238-243.

[17]杨进， 陈亮. 基于小波神经网络与ARIMA组合模型在股票预测中的应用[J]. 经济数学， 2018， 35（2）： 62-67.

[18]曹雷欣， 孙红兵. 基于灰色神经网络的股票收益率预测[J]. 计算机与数字工程， 2017， 45（1）： 24-28.

[19]卢嘉澍， 孙坤， 廉洁， 等. 基于灰度预测与马尔柯夫过程的股票价格预测模型[J]. 现代商业， 2017（17）： 74-75.

[20]严龙， 林丛， 朱佳慧. 马尔科夫链在金融投资中的应用[J]. 宁波工程学院学报， 2017， 29（4）： 1-8.

[21]杨晓， 杨德平. 基于Matlab图形用户界面的马氏链股价预测系统开发[J]. 青岛大学学报： 工程技术版， 2015， 30（3）： 43-49， 69.

Development of the Stock Price Trend Simulation System Based on Matlab GUI

ZHAO Buxiang， YANG Deping

（School of Economics， Qingdao University， Qingdao 266071， China）

Abstract：In order to develop a stock forecasting tool for stock practitioners and researchers， this paper develops a stock price simulation system based on Matlab GUI. By investigating the characteristics of the stock market， the types of forecasting models and the related variables， this paper selects random walk model， generalized Vinax process model， Geometric Brownian motion model and jump influence model to simulate the Stock Price Trend， and develops a Matlab GUI system with function as a tool for stock analysis. The results show that the price of the random walk model is uncertain， and for the Geometric Brownian motion and Vinax process with jumps， the price of a single simulation is stochastic， but the price of multiple simulation is certain. The interface is easy to operate， avoids the tedious modeling and calculation process， and is convenient for the participants of the stock market. This study has a promising application prospect.

Key words：random walk; wiener process; geometric Brownian motion; jump effect; GUI

收稿日期： 2019-12-17; 修回日期： 2020-02-15

作者簡介： 赵步祥（1990-），男，硕士研究生，主要研究方向为经济数理方法。

通信作者： 杨德平（1963-），男，副教授，硕士生导师，主要研究方向为金融计量。 Email： qduydp@126.com