基于模型参考自适应的四旋翼飞行器反步控制

李珺　王娜　宋欣　花玉

摘要：针对四旋翼飞行器易受干扰的问题，本文提出了一种基于模型参考自适应的反步控制方法，在外界气流干扰和内部参数不确定的情况下，保证四旋翼飞行器稳定平滑地跟踪参考信号。将四旋翼飞行器的飞行控制系统分解为水平位置控制子系统与高度和姿态控制子系统，并对两个子系统分别设计反步控制器，然后在高度和姿态控制子系统应用模型参考自适应控制，提高该子系统的抗干扰性能，从而进一步改善水平位置控制性能，同时采用Lyapunov稳定性理论，证明整个闭环系统渐近稳定。仿真结果表明，该算法能够有效抑制外界气流干扰，对负载不确定性具有较强的自适应能力，有效提高系统的稳定性和抗干扰性能。该研究具有一定的理论和实际应用价值。

关键词：四旋翼飞行器; 反步控制; 模型参考自适应控制; 抗干扰

中图分类号： TP273+.2文献标识码： A

近年来，由于四旋翼飞行器具有体积小、质量轻、可垂直起降和悬停等优点，在军用和民用领域应用越来越广泛[13]。但四旋翼飞行器是一种欠驱动、强耦合、多变量、非线性的复杂系统，并且受重力和陀螺效应等多种物理效应的影响及气流等外界环境的干扰[4]，对控制器的设计要求较高。因此，设计一种保障飞行器稳定飞行的控制器至关重要。国内外许多学者对四旋翼飞行器的控制做了大量的研究工作，王振华等人[5]设计了基于偏差的比例积分微分控制（proportional-integral-derivative control，PID）器，其作为最经典的控制方法，实现对飞行器的控制，但是对干扰的抑制能力较弱，鲁棒性不强;F. Alia等人[6]将四旋翼飞行器的控制系统分解为水平位置控制子系统与高度和姿态控制子系统，并在水平位置控制子系统加入模型参考自适应控制，解决了水平位置受到干扰时不能稳定飞行的问题，但高度和姿态控制子系统仍不能保证有较强的抗干扰能力;梁雪慧等人[7]设计了基于PID的姿态自适应控制器，而高度子系统控制器却要单独设计，增加了控制系统的复杂性。基于此，本文将四旋翼飞行器的飞行控制系统分解为水平位置控制子系统与高度和姿态控制子系统，由于四旋翼飞行器姿态角的变化直接影响到机体的位置和速度[89]，因此在分别给内外环控制子系统设计反步控制器的基础上，在内环子系统加入模型参考自适应控制，不仅使四旋翼飞行器的高度和姿态具有更高的抗干扰能力，而且消除了姿态角不稳定时对水平位置的影响。该系统解决了高度子系统控制器需要单独设计的问题，简化了控制器的结构，并且能够使高度和姿态控制子系统更加稳定。该研究为提高四旋翼飞行器的抗干扰性能奠定了理论基础。

1四旋翼飞行器动力学模型

1.1動力学模型

在地面坐标系下，四旋翼飞行器动力学模型[1013]为

式中，Cφ=cos φ，Sγ=sin γ，下同;x··、y··和z··分别为飞行器沿x轴、y轴和z轴方向的加速度;θ··、γ··和φ··分别为飞行器俯仰角、横滚角和偏航角加速度;θ·、γ·和φ·分别为俯仰角、横滚角和偏航角的角速度;m为飞行器的质量;g为重力加速度;jx、jy和jz分别为沿x轴、y轴和z轴的转动惯量;l为机架长度。

1.2四旋翼飞行器动力学模型的简化和分析

四旋翼飞行器由4个正交布置的电机驱动[1415]，根据四旋翼飞行器飞行时的实际情况，各姿态角均为小角度，可进行如下简化：Sθ=θ，Sγ=γ，Sφ=φ，Cθ=1，Cγ=1，Cφ=1。同时，飞行器飞行的加速度较小，γφ，θφ，θγ为高阶小量，可近似为0，四旋翼飞行器关于机体x轴、y轴对称，所以jx-jy=0。将上述分析代入式（1）。

四旋翼飞行器是典型的欠驱动系统，具有6个自由度，却只有4个独立的控制输入，仅能控制四旋翼飞行器的4个自由度[1618]，也只能保证4个自由度的稳定性。四旋翼飞行器的高度方向由U1完整驱动，飞行器姿态θ，γ，φ由U2，U3，U4完整驱动，飞行器水平位置x，y由飞行器姿态角和U1决定，因此水平位置与姿态角和高度耦合[1920]。

2基于模型参考自适应的四旋翼飞行器反步控制系统设计

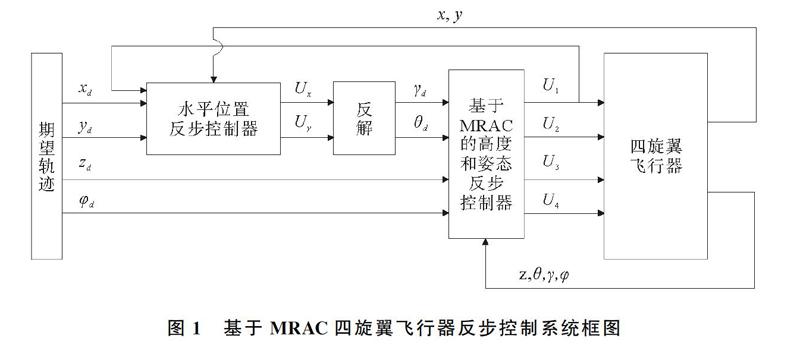
四旋翼飞行器的飞行控制系统分解为内环与外环控制子系统，对基于模型参考自适应（model reference adaptive control，MRAC）的四旋翼飞行器反步控制系统进行设计，基于MRAC四旋翼飞行器反步控制系统框图如图1所示。内环为高度和姿态控制子系统，外环为水平位置控制子系统，对2个子系统分别设计反步控制器，然后在高度和姿态控制子系统加入模型参考自适应控制，抑制参数变化和外界气流等因素对该子系统的干扰，消除姿态角不稳定时对水平位置的影响。

2.1四旋翼飞行器水平位置子系统反步控制器设计

四旋翼飞行器水平位置子系统的动力学方程为

2.2基于MRAC四旋翼飞行器高度和姿态子系统反步控制器设计

当系统的内部参数发生变化或受到外部气流干扰时，四旋翼飞行器的高度和姿态子系统反步控制器的控制性能变差，不能保证飞行器高度和姿态的稳定，以致影响整个系统。为此，将在高度和姿态子系统加入模型参考自适应控制，提高控制性能。

2.2.2高度和姿态子系统模型参考自适应控制器设计

模型参考自适应线性反馈控制律与反步控制律，共同构成四旋翼飞行器高度和姿态子系统控制器，即

式中，Uba为反步控制器控制输出;Uad为模型参考自适应控制器控制输出。其中，模型参考自适应控制器控制输出为

式中，K和F分别为前馈增益矩阵和反馈补偿矩阵;R为期望高度和姿态输入，具体为R=[0000zdθdγdφd]T;X为状态变量。

当高度和姿态子系统未加入模型参考自适应控制器，即Uad为0，且实际系统受到干扰时，矩阵Am和Bm会偏离理想值，影响系统的控制效果。模型参考自适应控制器将改善实际系统受干扰时的控制性能，将式（21）中Uad代入式（23），得

3.1四旋翼飞行器受到外部气流干扰时控制效果

由于外部气流的数学模型具有余弦特性，因此将四旋翼飞行器高度和姿态子系统4个通道加入的干扰设定为

四旋翼飞行器定点飞行水平位置响应曲线如图3所示，四旋翼飞行器定点飞行高度和姿态角响应曲线如图4所示。

由图3和图4可以看出，基于MRAC的反步控制器控制时，大约在仿真开始后的第1 s飞行器到达目标位置，并且飞行基本达到稳定状态。在反步控制器控制时，高度z约有01 m幅值振荡，而在基于MRAC的反步控制器控制时，高度z基本渐近稳定在指定高度1 m的位置。在俯仰角θ和横滚角γ通道，反步控制器对干扰的抑制效果非常好，在加入自适应控制后，俯仰角和横滚角对指令的响应阶段比反步控制的控制效果更佳，极大地减小了系统的超调量。在偏航角φ通道，相比反步控制器，基于MRAC的反步控制器对不确定干扰有很好的抑制效果。仿真结果表明，基于MRAC的反步控制器极大地提高了系统的抗干扰性能，验证了所提算法的有效性。

四旋翼飞行器在负载变化时高度响应曲线如图5所示。由图5可以知，当四旋翼飞行器在5 s时，负载减少30%，飞行器质量发生突变。在反步控制器控制时，飞行器偏离高度指令，上升约01 m，而在基于MRAC的反步控制器控制时，高度未发生变化，始终稳定在指令高度上，模型参考自适应很好地弥补了反步控制器的不足。仿真结果表明。基于MRAC的反步控制器，能有效消除飞行器质量等内部参数改变时对飞行器稳定飞行产生的影响，验证了所提算法的有效性。

4结束语

本文通过简化和分析四旋翼飞行器的动力学方程，设计了基于模型参考自适应的四旋翼飞行器反步控制器。在四旋翼飞行器设计反步控制器的基础上，加入模型参考自适应控制，有效抑制了干扰，保证四旋翼飞行器对指令信号的稳定平滑跟踪。仿真结果表明，相对于反步控制，该算法能够有效提高系统的稳定性和抗干扰性能，具有一定的理论研究和实际应用价值。为进一步提高四旋翼飞行器的抗干扰性能，对不同类型干扰的分析是接下来工作的方向。

参考文献：

[1]石川， 林达. 基于自适应积分反步的四旋翼飞行器控制[J]. 计算机应用研究， 2018， 5（11）： 33383342.

[2]Zhao B， Xian B， Zhang Y， et al. Nonlinear robust adaptive tracking control of a quadrotor uav via immersion and invariance methodology[J]. IEEE Transactions on Industrial Electronics， 2015， 62（5）： 28912902.

[3]李艾棠， 谭功全， 郭金虎. 四旋翼无人机悬停飞行自适应PD控制器设计[J]. 四川理工学院学报， 2017， 30（6）： 5460.

[4]刘峤， 吴怀宇， 陈洋， 等. 基于反步法与参考模型的四旋翼飞行器自适应滑动模态控制[J]. 高技术通讯， 2018， 28（7）： 633642.

[5]王振华. 基于DSP的微型飞行控制器设计研究[D]. 南京： 南京航空航天大学， 2013.

[6]Ghaffar A A， Richardson T. Position tracking of an underactuated quadrotor using model reference adaptive control[C]∥AIAA Guidance， Navigation， and Control Conference. San Diego. California， USA： American Institute of Aeronautics and Astronautics， 2016.

[7]梁雪慧， 李景濤， 党媛媛. 四旋翼飞行器姿态稳定自适应控制研究[J]. 计算机仿真， 2017， 34（8）： 7579.

[8]刘苏漫， 杨晓慧， 李文明. 四旋翼飞行器反步自适应PID控制[J]. 电光与控制， 2019， 26（2）： 7679.

[9]滕雄， 吴怀宇， 陈洋， 等. 基于反步法的四旋翼飞行器轨迹跟踪研究[J]. 计算机仿真， 2016， 33（5）： 7883.

[10]岳基隆. 四旋翼无人机自适应控制方法研究[D]. 长沙： 国防科学技术大学， 2010.

[11]Cabecinhas D， Cunha R， Silvestre C. A trajectory tracking control law for a quadrotor with slung load[J]. Automatic， 2019， 106： 384389.

[12]Wang N， Deng Q， Xie G M， et al. Hybrid finite-time trajectory tracking control of a quadrotor[J]. ISA Transactions， 2019， 90： 278286.

[13]许玥， 甄子洋， 杨政. 基于自适应控制的无人机自动驾驶仪控制系统： 中国， CN 201710610691. 0[P]. 20171208.

[14]Nicol C， Mncnab C J B， Ramirez-Serrano A. Robust adaptive control of a quadrotor helicopter[J]. Mechatronics， 2011， 21（6）： 927938.

[15]Pounds P， Mahony R， Corke P. Modeling and control of a quadrotor robot[J]. Control Engineering Practice， 2010， 18（7）： 691699.

[16]史鲲， 张效义， 陈勇， 等. 空面导弹模型参考自适应控制设计与仿真[J]. 飞行力学， 2010， 28（3）： 5154.

[17]陈国定， 程嘉辉， 张晓峰， 等. 四旋翼无人机飞行姿态模型参考自适应控制[J]. 计算机系统应用， 2015， 24（11）： 247251.

[18]姜明瑞. 四旋翼无人机轨迹跟踪控制系统设计[D]. 吉林： 长春理工大学， 2018.

[19]Liu H， Tian Y， Lewis F L， et al. Robust formation tracking control for multiple quadrotors under aggressive maneuvers[J]. Automatica， 2019， 105： 179185.

[20]李瑞琪， 王洪福， 李瑞雪， 等. 基于模型参考自适应的四旋翼飞行器控制[J]. 计算机测量与控制， 2013， 21（12）： 32603271.

[21]梁雪慧， 党媛媛， 赵嘉祺. 四旋翼飞行器模型参考自适应容错控制[J]. 电光与控制， 2018， 25（7）： 8891.

Model Reference Adaptive-Based Backstepping Control for Quadrotor

LI Jun， WANG Na， SONG Xin， HUA Yu

（School of Automation， Qingdao University， Qingdao  266071， China）

Abstract：  For the quadrotor is vulnerable， a model reference adaptive-based backstepping control method for quadrotor was proposed. The quadrotor were guaranteed to track the reference signal quickly and smoothly under the influence of external airflow interference and internal parameter uncertainty. The flight control system of the quadrotor was decomposed into horizontal position control subsystem and height and attitude control subsystem. The backstepping controllers for two subsystems were designed， respectively. Then， the model reference adaptive control（MRAC） was applied to the height and attitude control subsystem to improve the anti-interference performance， and further improve the control performance of the horizontal position of the quadrotor. Finally， the asymptotic stability of the closed-loop system was proved by using Lyapunov stability theory. The simulation results show that the algorithm can effectively suppress the external airflow interference， and it has strong adaptive ability to load uncertainty. This algorithm effectively improves the stability and anti-interference performance of the system， and has certain theoretical research and practical application value.

Key words：  quadrotor; backstepping control; MRAC; anti-interference

收稿日期： 2019-12-17; 修回日期： 2020-01-16

基金項目：山东省自然科学基金资助项目（ZR2016FP10）;国家自然科学基金青年科学基金项目（61703221）

作者简介：李珺（1992-），男，山东淄博人，硕士研究生，主要研究方向为四旋翼飞行器控制算法。

通信作者：王娜（1983-），女，博士，讲师，硕士生导师，主要研究方向为鲁棒抗干扰控制和飞行器姿态控制等。Email： wangnaflcon@126.com