时滞矩形广义系统的混合H∞与无源控制

黎婕　林崇　刘焕霞

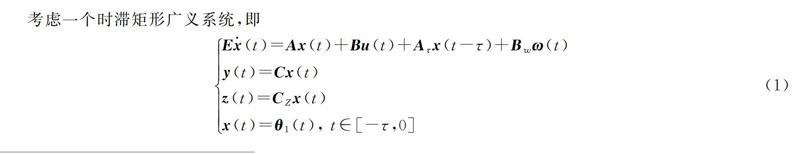
摘要：針对时滞矩形广义系统的混合H∞与无源控制问题，本文通过构造带时滞的动态补偿器，利用实数域上正常广义系统的可容许性判据，得到可使闭环系统在混合H∞与无源性能指标γ条件下容许的充分条件。通过构建合适的LyapunovKrasovskii泛函，结合放松过的Wirtinger不等式，对泛函导数积分项进行处理，将不等式中非线性项进行代换，最后通过数值算例验证该方法的有效性，并将混合H∞与无源控制问题从正常广义系统推广到时滞矩形广义系统。验证结果表明，本文所得到的稳定性充分条件拥有更大的时滞上界，决策变量更少，保守性和复杂度更低。该研究对时滞矩形广义系统的稳定性分析与控制器设计问题具有重要意义。

关键词：矩形广义系统; 混合H∞与无源控制; 时滞; 动态补偿

中图分类号： TP13; N941.1 文献标识码： A

文章编号： 10069798（2020）02000108; DOI： 10.13306/j.10069798.2020.02.001

广义系统，又称广义状态空间系统，与常规系统相比，可以更好地描述物理系统，因而一直受到广泛研究和关注[12]。而矩形广义系统，作为一类更广泛的广义系统，由于状态变量个数与状态方程个数不一致，因而具有更复杂的行为[3]。从20世纪80年代末开始，矩形广义系统开始受到关注，很多学者着手研究矩形系统的正则性及广义正则化问题[34]，矩形广义系统脉冲能控性、能观性问题[56]，以及滤波、估计问题和观测器设计问题等[79]。Zhang G S等人[1011]首次提出用动态补偿方法使闭环矩形广义系统正则化;Chen J等人[12]设计了矩形TS模糊离散系统的时滞动态补偿器;Zhang X F等人[1314]又将矩形广义系统相关理论延伸到分数阶领域。由于时滞存在于许多动力系统中，经常导致性能不佳和不稳定，因此研究时滞矩形广义系统的稳定性具有重要的理论和现实意义。近年来，随着线性矩阵不等式（linear matrix inequality，LMI）方法的发展，许多学者对各种系统的H∞控制问题进行了广泛研究[1516]。Xu S等人[1718]对连续和离散时间时滞系统的耗散进行分析和设计;Wu Z G等人[1920]讨论了连续和离散时滞广义系统的混合H∞与无源滤波问题;Chen J等人[21]研究了时滞广义系统的混合H∞与无源控制问题。针对时滞矩形广义系统的混合H∞与无源控制问题，目前还没有学者对其作相应的研究。基于此，本文将正常广义系统推广到时滞矩形广义系统，并利用带时滞的动态补偿器，得到在混合H∞与无源性能指标γ下使闭环系统容许的充分条件，实现了混合H∞与无源控制，并通过数值例子验证了本文结果有效性。该研究为时滞矩形广义系统的稳定性提供了理论依据。

5 结束语

本文针对时滞矩形广义系统设计了一类动态补偿器来实现闭环系统的混合H∞与无源性能控制问题。在文献[21]的基础上，首次把混合H∞与无源控制问题推广到矩形广义系统中，并利用动态补偿器实现了系统的渐近稳定。与文献[21]相比，本文方法引入了新的自由权矩阵，并采用一种有效算法来计算控制器增益矩阵，所得结果拥有更大的时滞上限，决策变量更少，保守性更低，数值算例证明了该结果的有效性。另外，本文是在文献[27]针对矩形广义系统镇定问题的研究基础上，进一步考虑了带时滞的矩形广义系统的控制问题。这类问题目前研究成果并不多，将其与实际生产模型相结合可以作为进一步研究的方向。

参考文献：

[1]Dai L. Singular control systems[M]. Berlin： Springer-Verlag， 1989.

[2]Xu S， Lam J. Robust control and filtering of singular systems[M]. Berlin： Springer-Verlag， 2006.

[3]Fletvher L R. Regularizability of descriptor systems[J]. International Journal of Systems Science， 1986， 17（6）： 843847.

[4]Duan G， Chen Y. Generalized regularity and regularizability of rectangular descriptor systems[J]. Journal of Control Theory and Application， 2007， 5（2）： 159163.

[5]Ishihara J Y， Terra M H. Impulse controllability and observability of rectangular descriptor systems[J]. IEEE Transactions Automatic Control， 2001， 46（6）： 991994.

[6]Hou M. Controllability and elimination of impulsive modes in descriptor systems[J]. IEEE Transactions Automatic Control， 2004， 49（10）： 17231727.

[7]Darouach M. H∞ unbiased filtering for linear descriptor systems via LMI[J]. IEEE Transactions Automatic Control， 2009， 54（8）： 19661972.

[8]Hsieh C S. H∞ kalman estimation for rectangular descriptor systems with unknown inputs[J]. IEEE Transactions Automatic Control， 2014， 59（3）： 826832.

[9]Gupta M K， Tomar N K， Bhaumik S. Full and reduced-order observer design for rectangular descriptor systems with unknown inputs[J]. Journal of the Franklin Institute， 2015， 352（3）： 12501264.

[10]Zhang G S. Regularizability controllability and observability of rectangular descriptor systems by dynamic compensation[C]∥Proceedings of the American Control Conference. Minneapolis， MN， USA： 2006： 43934398.

[11]Zhang G S， Liu L. Linear quadratic optimal control based on dynamic compensation for rectangular descriptor systems[J]. Acta Automatica Sinica， 2010， 36（2）： 17521757.

[12]Chen J， Lin C， Chen B， et al. Regularization and stabilization for rectangular TS fuzzy discrete-time systems with time delay[J]. IEEE Transactions on Systems Man & Cybernetics Systems， 2019， 49（4）： 833840.

[13]Zhang X F， Zhao Z L. Normalization and stabilization for rectangular singular fractional order T-S fuzzy systems[J]. Fuzzy Sets and Systems， 2020， 381： 140153.

[14]Zhao Z L， Zhang X F， Wang Q G. Output feedback stabilization of uncertain rectangular descriptor fractional order systems with 0 < a < 1[J]. IEEE Access， 2019： 108948108955.

[15]Ma Y， Fu L， Jing Y， et al. Finite-time H∞ control for a class of discrete-time switched singular time-delay systems subject to actuator saturation[J]. Appl Math Comput， 2015， 261： 264283.

[16]Shao Y Y， Liu X D， Sun X， et al. A delay decomposition approach to H∞ admissibility for discrete-time singular delay systems[J]. Information Sciences， 2014， 279： 893905.

[17]Xu S， Zheng W X， Zou Y. Passivity analysis of neural networks with time-varying delays[J]. IEEE Trans. Circuits Syst II Exp Briefs， 2009， 56 （4）： 325329.

[18]Wu Z G， Park J H， Su H， et al. Admissibility and dissipativity analysis for discrete-time singular systems with mixed time-varying delays[J]. Appl Math Comput， 2012， 218 （13）： 71287138.

[19]Wu Z G， Park J H， Su H， et al. Mixed H∞ and passive filtering for singular systems with time delays[J]. Signal Process， 2013， 93： 17051711.

[20]Shi P， Zhang Y， Chadli M， et al. Mixed h-infinity and passive filtering for discrete fuzzy neural networks with stochastic jumps and time delays[J]. IEEE Transactions on Neural Networks and Learning Systems， 2016， 27（4）： 903909.

[21]Chen J， Lin C， Chen B， et al. Mixed H∞ and passive control for singular systems with time delay via static output feedback[J]. Applied Mathematics and Computation， 2017， 293： 244253.

[22]Meisami-Azad M， Mohammadpour J， Grigoriadis K M. Dissipative analysis and control of state-space symmetric systems[J]. Automatica， 2009， 45（6）： 15741579.

[23]Chang X H， Ju Hyunseok， Zhou J P. Robust static output feedback H∞ control design for linear systems with polytopic uncertainties[J]. Systems & Control Letters， 2015， 85： 2332.

[24]Park P G， Lee W I， Lee S Y. Auxiliary function-based integral inequalities for quadratic functions and their applications to time-delay systems[J]. Journal of the Franklin Institute， 2015， 352（4）： 13781396.

[25]Zheng F， Wang Q G， Lee T H. On the design of multivariable PID controllers via LMI approach[J]. Automatica， 2002， 38（3）： 517526.

[26]Sakthivel R， Joby M， Mathiyalagan K， et al. Mixed H∞ and passive control for singular Markovian jump systems with time delays[J]. Journal of the Franklin Institute， 2015， 352（10）： 44464466.

[27]Lin C， Chen J， Chen B， et al. Stabilization for a class of rectangular descriptor systems via time delayed dynamic compensator[J]. Journal of the Franklin Institute， 2019， 356（4）： 19441954.

Mixed H∞ and Passive Control for Stabilization for Time-Delay Rectangular Descriptor Systems

LI Jie， LIN Chong， LIU Huanxia

（Institute of Complexity Science， Qingdao University， Qingdao 266071， China）

Abstract：  Aiming at the problem of mixed H∞ and passive control for time-delay rectangular descriptor systems， this paper constructs a dynamic compensator with time delay and uses the admissibility criterion of a normal singular system to obtain sufficient conditions under mixed H∞ and passive performance index γ requirements. Firstly， a suitable Lyapunov-Krasovskii functional is constructed in this paper. Then， the derivative term of the functional derivative is processed in combination with the relaxed Wirtinger inequality， and then the non-linear term in the inequality is replaced. Finally， numerical example verifies the validity of the method. In this paper， the mixed H∞ and passive control problem is extended from a normal singular system to a rectangular descriptor system with time delay. The verification results show that the method in this paper has a larger upper bound on time delay， fewer decision variables， and lower conservatism and complexity than the sufficient stability conditions obtained by the existing results. This research is of great significance to the stability analysis and controller design of rectangular descriptor systems with time delay.

Key words：  rectangular descriptor systems; mixed H∞ and passive control; time delay; dynamic compensation

收稿日期： 2019-12-02; 修回日期： 2020-02-4

基金項目：国家自然科学基金资助项目（61673227，61873137）

作者简介：黎婕（1995-，女，硕士研究生，主要研究方向为矩形广义系统的分析与控制。

通信作者：林崇（1967-），男，博士，教授，硕士生导师，主要研究方向为系统理论与控制理论。 Email： linchong_2004@hotmail.com