暗像素先验的模糊图像盲复原方法

涂春梅，陈国彬，刘 超

1.重庆工商大学 融智学院，重庆市生态环境规划空间信息管理与决策支持重点实验室，重庆 401320

2.贵州航天电器股份有限公司，贵阳 550009

1 引言

图像的盲去模糊旨在从一幅模糊的图像中复原出一幅清晰的图像以及估计出一个准确的模糊核。这是一个经典的图像信号处理问题，在过去的几十年中，在视觉和图形领域已经成为一个研究热点。并且随着手持摄像机（特别是智能手机）拍摄的图片的增多，去模糊问题的重要性也与之俱增，因此有必要研究怎么对图像去除模糊以得到一幅高质量的清晰图像[1]。

众所周知，图像模糊的过程可以用以下的数学模型来表示：

其中，B、I、k和n分别代表观察到的模糊噪声图像、原始的清晰图像、模糊核和噪声。表示卷积操作。在模糊图像的盲去模糊中，因为只有B是已知的，而需要同时复原出I和k，所以该问题是一种严重的病态逆问题。为了能够有效地实现模糊图像的盲去模糊，需要对待复原的清晰图像和模糊核给出正确的先验约束。例如，大量的方法假设待复原清晰图像的梯度具有稀疏特性，因此提出了一种严重拖尾分布的图像先验，并结合最大后验概率（Maximum a Posterior，MAP），来估计原始的清晰图像。但是Levin 等人也指出，这类去模糊方法并不能真正实现模糊图像的清晰化复原，因为这种严重拖尾分布的图像先验会让最终求解出的图像趋向于偏爱模糊图像而不是原始的清晰图像[2]。为了改进这个问题，人们开始研究一些新的图像先验，以保证新的图像先验会偏爱原始清晰图像而不是模糊的图像，例如归一化的稀疏先验、L0 范数先验和内部图像块的复现先验等。Fergus 等人利用一种混合的高斯分布来学习图像梯度的先验，实现了模糊图像的盲复原，但是该方法的计算量太大[3]。Krishnan 等人提出了一种基于L1 范数和L2 范数的归一化的图像稀疏先验，能够强制复原图像趋向于清晰的图像而非模糊的图像[4]。Xu等人提出了一种L0范数作为复原图像的先验[5]。Ma等人提出了一簇稀疏函数来作为复原图像的先验，对复原图像的梯度进行稀疏性约束[6]。实验证明该类函数先验具有与Xu 等人提出的L0 范数[5]相似的特性，均会偏爱清晰的图像而不是模糊的图像。Pan 等人将L0 范数同时运用到了复原图像的空间域和梯度域中，进一步强制复原图像远离模糊[7]。Michaeli等人利用图像不同尺度上模糊程度也会不同的特性，提出了一种内部图像块复现的先验来约束复原图像趋向于清晰化[8]。Zuo等人提出了一种逐次迭代的模糊图像盲复原方法。该方法通过学习找到每个尺度上每次迭代中所需的最优的图像稀疏先验[9]。除了新的图像先验以外，近几年，一种启发式的边缘选择并结合MAP 的模糊图像盲复原方法被提出，并引起了广泛的关注。该类方法不仅能够有效实现模糊图像的盲复原，同时还具有计算量较小的优势。Cho等人在进行盲复原之前，提出了一种额外的图像边缘选择步骤：利用双边滤波器、shock滤波器和梯度阈值的方法来首先提取出图像中的显著边缘，然后仅利用提取出的边缘来进行模糊核的估计[10]。Xu等人基于图像边缘与模糊核在空间尺度方面的关系，提出了一种基于空间尺度的图像边缘提取方法。实验证明了该方法提取出的边缘能够有效复原出清晰的原始图像，并估计出准确的模糊核[11]。Sun 等人利用图像块的先验，提出了一种基于块先验的边缘提取方法以实现模糊核的准确估计，进而实现模糊图像的清晰化复原[12]。Pan等人利用外部的清晰图像数据库来拟合模糊图像中的有利边缘，实现了人脸图像的去模糊复原[13]。

通过对现有方法的分析可知，它们几乎都存在一种缺点：现有的图像先验几乎都是基于统计的方式得到的[3-9，12-13]。因此现有方法都会倾向于某种特定的应用领域，即对于不同内容或者不同类型的模糊图像，其复原效果是不同的，普适性较差。

2 基于暗像素先验的模糊图像盲复原模型

为了能够让读者更好地理解本文提出方法的原理，接下来，将首先对暗像素进行定义：

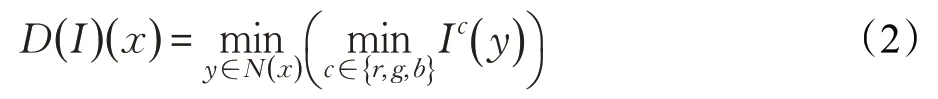
其中，x和y表示图像I中像素点的位置，是一个以x为中心的图像块，Ic是图像I的第c个颜色信道。如果I是一幅灰度图像，那么由式（2）可知，图像中的暗像素其实就是一个图像块中像素值最小的像素。

由式（1）可知，模糊图像是由清晰图像与模糊核的卷积所产生的。既然是卷积运算，那么对于数字图像（离散信号）来说，卷积操作是对其中一个信号进行反转和平移，然后将反转、平移后的信号与另一个信号进行对应元素的相乘，再将其乘积全部相加后的结果：

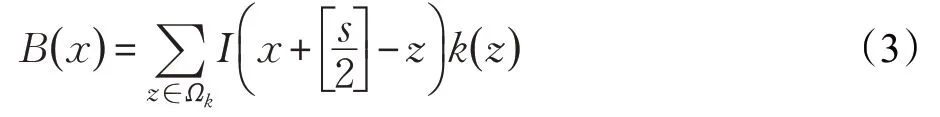
其中，Ωk和s分别表示模糊核k的支持域和大小，是四舍五入操作。可以注意到：一方面，由式（3）可知，图像I模糊的过程可被看作是图像I的局部权重线性组合的和；另一方面，由模糊的过程（式（1））、卷积的定义（式（3））和暗信道的定义（式（2））可知，与清晰图像相比，模糊图像中暗像素的像素值会比清晰图像中暗像素的像素值大。因为在一个局部的窗口中，像素值的权重和一定会大于或者等于该局部窗口中的最小像素值，即卷积运算增加了暗像素的像素值。因此，得到如下结论：如将作为复原图像的先验，那么对进行最小化，即可强制复原图像远离模糊而向清晰化的方向发展，最终得到清晰锐化的复原图像。接下来，用数学的方法来证明在区分清晰图像和模糊图像方面的能力：

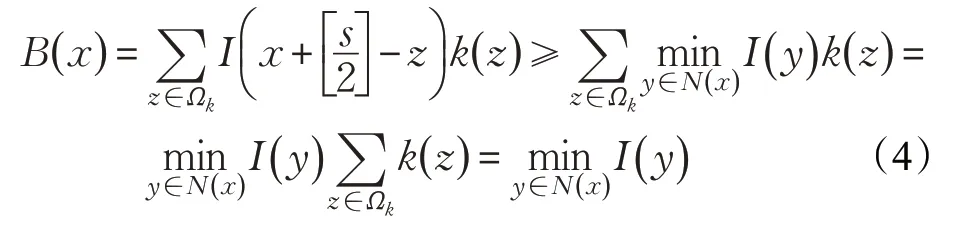
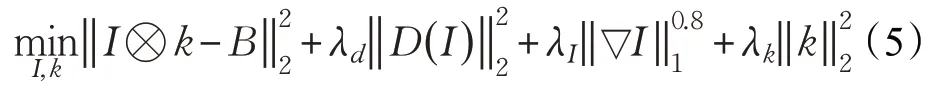
3 对提出模型的求解

对提出模型（5）的求解是较为困难的，这是由于超拉普拉斯先验和非线性函数。因此，为了实现对提出模型的有效求解，本文采用了一种变量分裂的策略：引入两个辅助变量，然后引入两个额外的约束和，那么，提出的模型（5）可被转换为式（6）：

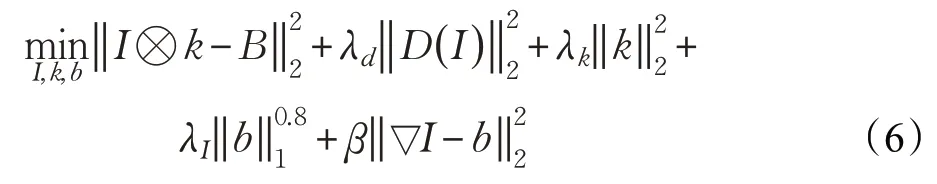
其中，β为惩罚参数。接下来将交互式地迭代求解I、k和b。文献[4-13]已经证明，利用变量分裂的策略能够让式（6）的解收敛于式（5）的解，因此本文采用的最优化方法所引起的误差可以忽略不计，对模糊图像盲复原方法的性能几乎没有影响。

（1）固定I和k，那么b可通过求解下式得到：

很明显，式（7）是一种典型的非凸的稀疏编码问题，因此可采用广义的迭代收缩算法[9]对其进行求解：

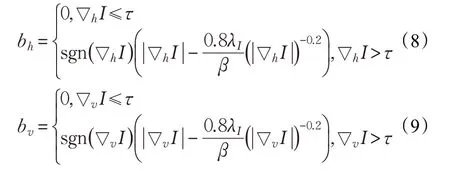
（2）固定b和k，那么I可通过求解下式得到：

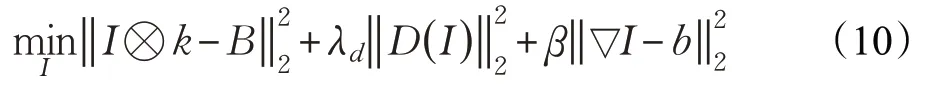
很明显，式（10）是一个二次性的方程，因此可直接对I求导来进行求解，但是难点却是如何求解非线性函数。通过研究发现，对图像I进行非线性操作等效于将一种线性操作符M作用到图像I的向量化形式上，。让M为：

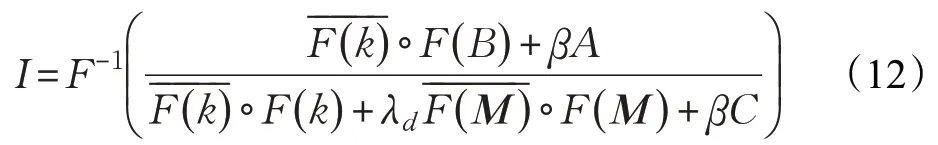
（3）固定I和b，那么k可通过求解下式得到：

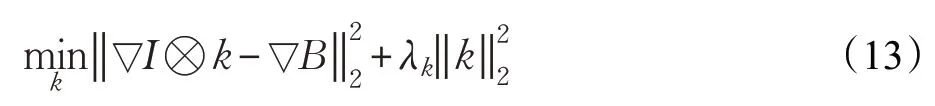
同样的，式（13）是一个二次性的方程，因此可采用与求解I相同的方法，直接对k求导，并采用快速傅里叶变换得到：

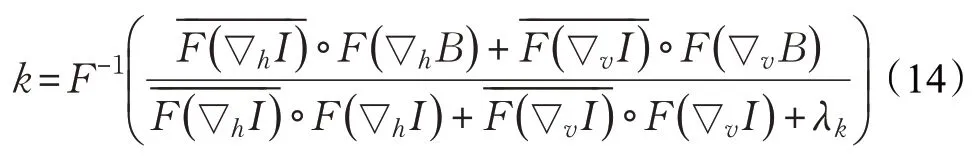
然后对求解得到的k再进行非负性和归一化的处理：

4 实验结果及分析

将本文提出的方法在文献[2]和文献[14]两个自然图像的数据集上进行了实验，并将提出的方法与文献[5]、文献[7]和文献[11]三种最近较为成功的盲复原方法进行了比较。因为实验的数量很大，所以本文只给出了其中的一部分实验结果来进行主观视觉的比较。除此之外，针对数据集[2]和[14]中的所有实验，本文还采用了逆卷积错误率（Deconvolution Error Ratio，DER）和自相似性测量（Self-Similarity Measure，SSIM）两种客观的评价指标来评价本文提出方法的性能。DER 和SSIM 的定义如下：

其中，Iest_res和Itur_res分别表示用估计的模糊核得到的复原图像和用真实的模糊核得到的复原图像。本文实验中所有图像的像素值都被归一化到0～1之间。

4.1 参数设置

本文提出的方法共涉及到 4 个参数λI、λd、λk和β。其中λI=λd=0.004,λk=2 。对于参数β,β0=2λu，然后在每次迭代之后对其进行加倍，βt=2βt-1,t为迭代次数，直到达到βmax=105为止。

4.2 文献[2]和文献[14]图像数据集上的实验

文献[2]和文献[14]的图像数据如图1 和图2 所示，图3所示为两个图像数据库中所用到的8种模糊核。由图1、图2和图3可知，该图像数据库总共可产生64幅模糊图像。这64 幅模糊的图像是人为产生的，因此本节的实验也称为人造模糊图像的实验。本文对所有的64幅人造运动模糊图像均进行了比较实验，但是因为篇幅的原因，这里只给出了其中一幅复原图像和与之对应的估计的BK（Blur Kernel）的主观视觉效果比较图，如图4所示。

如图4（b）和4（c）所示，文献[5]和文献[7]的方法所估计的模糊核均出现了不完整的现象：尾部消失，没有估计出来。同时文献[7]方法所估计的模糊核还出现了横竖交叉的瑕疵。因为不准确的模糊核估计，导致文献[5]和文献[7]方法所复原出的图像也出现了明显的振铃瑕疵，特别是在复原图像的边缘部分（请看右下角门框的周围）。文献[11]方法估计的模糊核更是出现了断裂，其最终的复原图像也不可避免地出现了严重的振铃瑕疵。相比之下，本文提出的方法因为有了暗像素的先验，所以能够有效地强制复原图像远离模糊而向清晰化的方向发展，从而得到清晰锐化的复原图像，进而能够有效地避免模糊核的断裂，并且能够有效地估计出模糊核的尾部，保证了模糊核的准确估计，所估计的模糊核是最准确的。而准确的模糊核又能反过来促进复原图像的进一步清晰和锐化，因此，如此交互式地迭代便是一种有效的良性循环，保证了在估计出准确模糊核的同时，复原出更高质量的清晰锐化图像。不仅清晰、锐化，而且有效抑制了振铃瑕疵（图4（e）右下角门框的周围），且最接近用真实模糊核得到的复原图像（图4（f））。图4在给定的数据集上证明了本文方法较近几年一些极具代表性的模糊图像盲复原方法相比，具有最佳的主观视觉效果。

图1 文献[2]的图像数据

图2 文献[14]的图像数据

图3 八种不同的模糊核

图4 所有方法在Corridor图像和模糊核6上的实验结果

接下来，将采用DER和SSIM评价指标来客观评价本文方法的性能。图5 所示为所有方法在文献[2]和文献[14]两个数据集和8 种不同的模糊核上的DER 百分比，其中横坐标2表示所有实验结果中DER小于2的百分比。如文献[2]中所说，DER小于2即证明复原图像的质量较好，大于2 且越大，则表明复原图像的质量越差。如图5所示，本文方法在所有的64幅人造模糊图像中，DER 小于2 的百分比是最高的，能够复原出最多的高质量复原图像。表1是所有方法在文献[2]和文献[14]两个数据集和8种不同的模糊核上所得到的平均SSIM值。由表1可以很明显地看到，本文方法在所有的64幅人造模糊图像的实验中，在绝大部分的情况下总能获得最高的平均SSIM 值（除了模糊核5）。图5 和表1 证明了在人造的模糊图像实验中，本文方法在客观的评价指标方面也是优于其他的模糊图像盲复原方法。

4.3 真实模糊图像的实验

为了进一步验证本文方法的性能，在真实的模糊图像上进行实验。

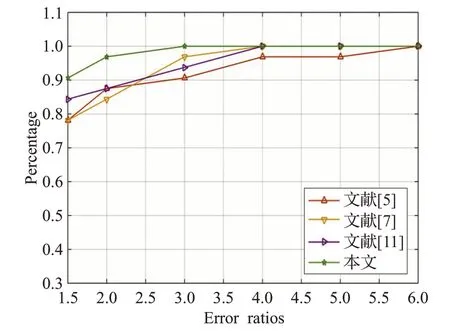
图5 所有方法在文献[2]和文献[14]数据集中的DER百分比

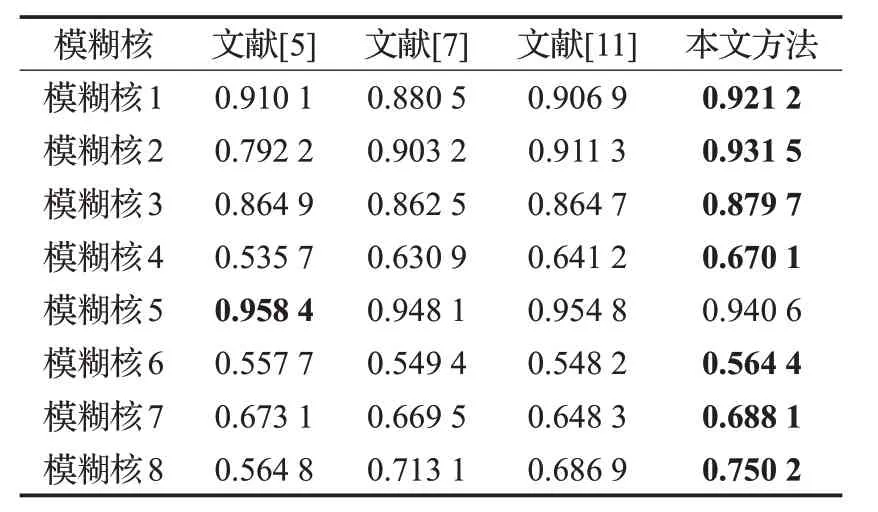
表1 所有方法在人造模糊图像盲复原的平均SSIM值

图6（a）为一幅真实的模糊图像，大小为685×561，BK的大小为97×97。如图6（b）和图6（c）所示，文献[5]方法和文献[7]方法所估计的模糊核出现了明显的间断。如图6（d）所示，文献[11]方法所估计的模糊核出现了明显的噪声。因此，文献[5]方法、文献[7]方法和文献[11]方法所得到的复原图像均出现了明显的振铃瑕疵（注意图中的局部放大部分）。相比之下，本文方法估计出了最准确的BK，不仅有效抑制了噪声，还很好地保证了模糊核的连续性，阻止了间断。同时，本文方法所得到的最后复原图像不仅具有最清晰锐化的边缘，同时还很好地抑制了振铃瑕疵（图6（e））。

图7（a）为另一幅大小为2 853×1 843 的真实模糊图像，其BK的大小为101×101。如图7（b）所示，文献[5]方法所估计的模糊核出现了断裂瑕疵，而文献[7]和文献[11]方法所估计的模糊核出现了明显的噪声瑕疵。因此，文献[5]、文献[7]和文献[11]方法所得的复原图像出现了明显的阴影瑕疵（图7（b）和图7（c））和明显的振铃瑕疵（图7（d））。相比之下，本文方法能够估计出最准确的模糊核，没有间断，也没有噪声等瑕疵。同时在最终的复原图像方面，本文方法不仅能够有效复原出清晰锐化的图像边缘和细节，同时还能够有效抑制阴影和振铃等瑕疵，获得最高质量的复原图像（图7（e））。

图6和图7从真实的模糊图像上进一步证明了本文方法的优越性。除了主观和客观的比较之外，表2利用在图6和图7中所有方法的运行时间来反映本文方法的复杂度。

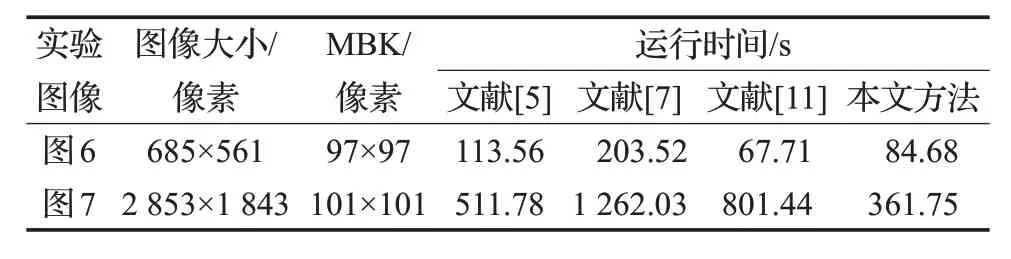
表2 所有方法在图6和图7的实验中的运行时间

如图6、图7 和表2 所示，虽然本文方法的时间略高于文献[11]的方法，但是估计和复原的效果都有较大的提升。而相比文献[5]和文献[7]，本文方法无论是在运行时间上还是在估计和复原的效果上都优于这两种方法。因此综合复原效果和运行时间，本文提出的方法具有更好的性能。

5 结束语

图像的盲去模糊问题是一个长期的且具有挑战性的逆问题。为了能够从模糊图像中有效地复原出原始的清晰图像，本文基于模糊图像的内在本质特性——模糊图像的暗像素是非稀疏的，提出了一种基于暗像素先验的模糊图像盲复原方法。因为本文提出的方法是基于模糊的内在特性，所以该先验不仅能够获得更好的复原效果，而且还能够适用于大量的模糊图像，具有更好的普适性。但是，提出的模型会导致一种非凸和非线性的最优化问题，因此，本文引入了一种最小化操作的线性近似来实现提出模型的最优化求解。大量的实验证明了本文方法与近几年一些极具代表性的模糊图像盲复原方法相比，有更好的性能。如何将本文方法扩展到模糊视频的清晰化复原中是接下来研究工作的重点。

图6 真实模糊图像的实验结果和局部放大图

图7 真实模糊图像的实验结果和局部放大图