混合粒子群和改进细菌觅食的不平衡数据分类

黄建琼，郭文龙

1.福州外语外贸学院 理工学院，福州 350202

2.福建江夏学院 电子信息科学学院，福州 350108

1 前言

在机器学习中，将数据集类别分布不平衡的现象称为不平衡问题。采用传统算法解决此类问题时，分类结果往往偏向多数分类，导致少数分类无法被正确识别出来。此外，传统算法基本是基于总体分类最大化来训练分类器的，这样会忽略一些样本的错误分类，从而影响传统分类器的分类结果[1-3]。然而在许多实际应用中，少量样本却比大量样本更有价值，如银行欺诈用户识别、医学癌症诊断以及网络黑客入侵等[4-8]。

不平衡数据挖掘是数据挖掘中一个极其重要的问题，目前已有许多算法应用在数据挖掘上，如K-最近邻居算法(K-Nearest Neighbor，KNN)、决策树算法（Decision Tree，DT）、人工神经网络（Artificial Neural Network，ANN）和遗传算法（Genetic Algorithm，GA）等[9-13]。这些算法通常假设数据集中各种分类的分布是均衡的，且可忽略某些分类。对此，部分学者提出一些处理不平衡数据的优化方法，如调整训练数据集的规模，使用代价敏感的分类器和滚雪球等[14-16]。而这些方法仍可能造成一般规则中的信息丢失和其他类别的错误分类，并最终导致数据过度匹配以及因过多的具体规则而引发的表现不佳。针对传统的优化方法无法解决数据集面临的这些问题，智能优化算法随之而生。

近年来，一些文献提出了混合PSO 与BFO 方法研究最优化问题，如矿井自动化控制的主要参数最优化、电动机控制系统、伺服系统的PID参数最优化、电力系统稳定性优化、词袋模型优化及蛋白质亚细胞定位预测[17-21]；另有文献提出优化粒子群算法应用于SVM_ELM 模型及改进粒子群算法用于特征选择[22-23]。因为粒子群收敛速度快，搜索能力强，本文提出混合粒子群优化算法与改进的细菌觅食优化算法应用于不平衡数据分类，目的是找到一个有效的算法解决原始BFO容易陷入局部优化的问题，并最终提高不平衡数据的准确性。

粒子群优化算法（Particle Swarm Optimization，PSO）是由Eberhart博士和Kennedy博士提出的[24]。它是一种模拟社会行为的群体启发式算法，类似鸟群会聚集到最优位置，以实现在多维空间中找到准确的目标。细菌觅食优化算法（Bacterial Foraging Optimization，BFO）是Passino于2002年根据大肠杆菌在人体肠道觅食现象而提出的仿生智能算法[25]。BFO 算法主要包括趋化、聚集、复制和迁徙四个操作。细菌觅食趋化操作可加强细菌的局部搜索能力，但是细菌觅食的全局搜索能力只能通过迁徙来完成，且全局搜索能力受到迁徙概率的限制，因此容易陷入局部最优。

本文提出了混合粒子群优化算法与改进的细菌觅食优化算法应用于不平衡数据分类。数据预处理采用Borderline-SMOTE 和 Tomek Link 的方法。然后，利用所提出的算法对不平衡数据进行分类。因为PSO 具有较强的全局搜索能力、个体效应和群体效应，将PSO 结合到改进的BFO 中，可改进原始BFO 的趋化操作过程。其次，改进复制操作过程，提高优胜劣汰的选择标准。最后，改进迁徙操作过程，防止种群陷入局部最优，防止进化停滞。所提出的算法可提高原BFO的全局搜索能力和搜索效率，提升不平衡数据的分类准确度。研究目的是获得一个有效的算法来提高不平衡数据的准确性，以便解决原始BFO 容易陷入局部优化的问题。卵巢癌微阵列数据是卵巢癌症诊断的重要信息，本文利用实际卵巢癌微阵列数据进行分类。本文算法提高了卵巢癌诊断的准确率，有助于更准确地判断和理解医学中的卵巢癌信息。本研究可建立一个供医疗使用的数据库系统，以便于研究和跟踪每个卵巢癌患者的病史。

2 细菌觅食优化和粒子群优化算法介绍

本文提出的混合算法是结合粒子群优化算法与改进的细菌觅食优化算法，并将该算法应用于不平衡数据分类。下面简要描述粒子群优化算法与细菌觅食优化算法原理。

2.1 细菌觅食优化算法

细菌觅食优化算法（BFO）具有非常好的分类效果，是一种全局随机搜索的进化算法。BFO 算法主要通过使用趋化、聚集、复制和迁徙四个操作的迭代计算来解决优化问题[26]。在趋化操作中，大肠杆菌在觅食中有两个基本运动：游动和翻滚。

通常，在环境条件恶劣的区域中，细菌会更经常翻滚；在好的环境中，则更经常游动。设细菌的种群规模为S，则P(j,k,l)={θi(j,k,l)|i=1,2,…,S}，表示细菌种群S中，第i个细菌的第j次趋化操作、第k次复制操作及第l次迁徙操作。设H(i,j,k,l)表示第i个细菌在位置θ(j,k,l)的代价，Nc为趋化操作的一个方向上的细菌长度。那么，第i个细菌每一步的趋化操作可用以下式子表示：

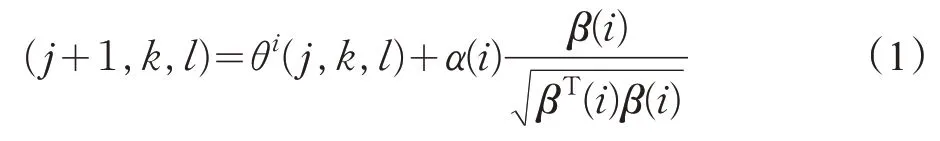
其中，α(i)>0 代表细菌向前游动的步长单位，β(i)代表细菌翻滚后的随机方向向量的单位向量。经过趋化操作步骤后，开始聚集操作过程，在聚集操作中，除了细菌自身的觅食方式外，每个细菌个体会收到群体中的其他个体发来的呼吁信号。因此，在BFO算法中，每一个细菌个体觅食的决策行为主要受到两个因素的影响：一是自身所获得的信息，即在单位时间内个体觅食的目的是最大化个体获得的能量；二是来自其他个体的信息，即通过群体中的其他细菌来传递觅食信息。其聚集操作用式（2）表达如下：

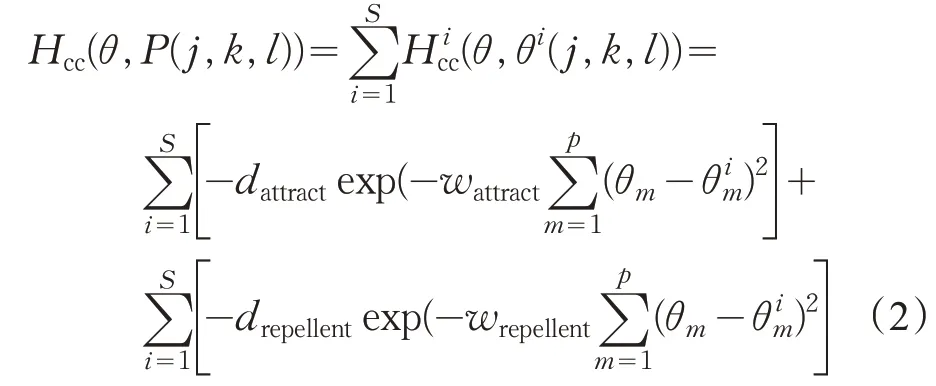
其中，Hcc(θ,P(j,k,l))是附加在实际代价函数上的惩罚值，θm表示最优细菌的位置，dattract、drepellent、wattract和wrepellent为可以被适当选择的不同的系数。在聚集操作中，Ns为生物学动机选择次数。聚集操作可用式子表示如下：

基于复制操作保持群体规模不变的原则，在复制过程中，按照细菌位置计算代价H的优劣排序，把排在后面的50%细菌淘汰掉，剩余的一半细菌进行自我复制，各自生成一个与自己完全相同的新个体，即生成的新个体与原个体有相同的位置，也就说具有相同的觅食能力。经过Nre复制步骤后，开始迁徙操作过程，设Ned为迁徙的步数，迁徙伴随着一定的概率Ped发生，当个体细菌满足迁徙的概率Ped，个体会死亡，并在解空间的任一位置随机产生一个新个体。新个体可能与原始细菌有不同的觅食能力，有利于跳出局部最优解。细菌觅食优化流程图如图1所示。

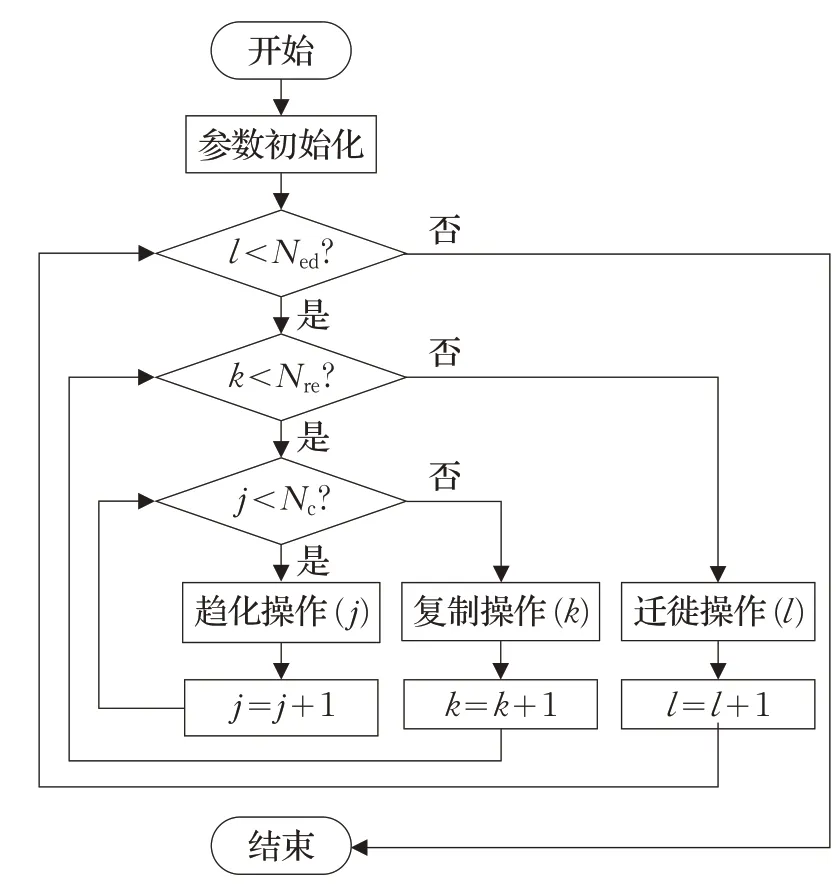
图1 细菌觅食优化算法的流程图

2.2 粒子群优化算法

粒子群优化算法（PSO）是一种学习鸟群在自然界中觅食的仿生算法，把鸟当成空间中一个粒子，鸟群就是粒子群。PSO是基于群体（群体中的每个个体又称为粒子）协作的随机搜索算法，粒子会在每一次迭代中更新自己[27]。为找到最优解，每个粒子根据它自身找到的最优位置(pbest)与其他所有成员找到的最优位置(gbest)这两个因素来改变它的搜索方向[28]。Shi等学者将pbest称为认知部分，gbest称为社会部分。每个粒子携带相应的信息，即它自己的速度和位置。粒子根据自身的相应信息，来决定它运动的距离和方向。粒子群优化算法（PSO）先初始化一组随机分布到待搜索的解空间中的粒子，包括个体最优位置pbest和全局最优位置gbest两个最优因素。个体最优位置是由每个粒子搜寻到的最优解，而全局最优位置则是由粒子群体获得的最优解。PSO算法采用正反馈机制，而使得它具有记忆功能。该算法原理简单，参数较少，且适用性较好。粒子根据以下的公式来更新自己的速度和位置[29]：

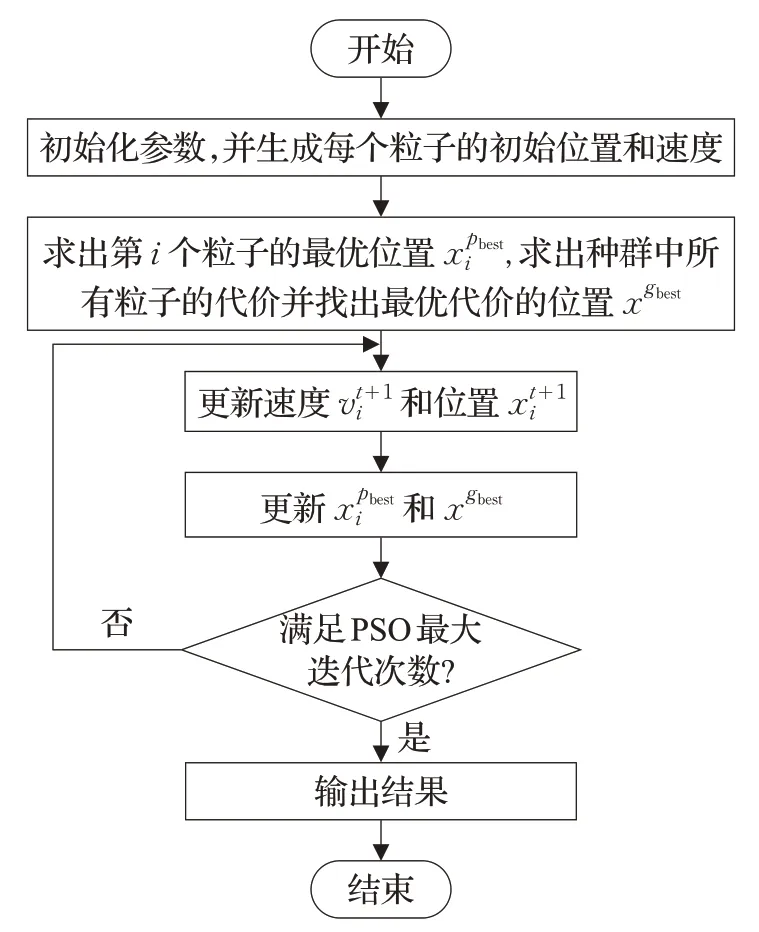
图2 粒子群优化算法的流程图

3 本文算法

针对BFO算法收敛速度慢以及易陷入局部最优的缺点，本文提出了将粒子群优化算法与改进的细菌觅食优化算法相结合，应用于不平衡数据的分类。本文旨在提高卵巢癌微阵列资料分类的准确度，并提高医生对卵巢癌微阵列资料判断的实用性和准确性。本文用三个数据集测试所提出算法的性能。一个是卵巢癌微阵列数据（ovarian cancer microarray data），另两个来自UCI数据库的垃圾电子邮件数据集（spam email dataset）和动物园数据集（zoo dataset）。卵巢癌微阵列数据来自某医院收集到的卵巢癌基因芯片真实数据，共有9 600个特征，不平衡率约为1∶20[30]。使用的微阵列数据实例包括卵巢组织、阴道组织、宫颈组织和子宫肌层，包括6例良性卵巢肿瘤（BOT）、10例卵巢肿瘤（OVT）和25例卵巢癌（OVCA）。垃圾电子邮件数据集和动物园数据集来自UCI 数据库。对于垃圾电子邮件数据集，共有4 601 封电子邮件，具有 58 个特征，如表 1 所示，不平衡率约为1∶1.54；对于动物园数据集，共有101 个实例，具有17个特征，如表2所示，不平衡率约为1∶25。

表1 垃圾电子邮件数据集的58个特征

表2 动物园数据集的17个特征

本文算法的流程图如图3 所示。首先进行参数初始化，数据预处理采用Borderline-SMOTE和Tomek Link的方法，并应用本文算法对不平衡数据进行分类。为了对少数类进行过采样，设计了Borderline-SMOTE，其主要思想是通过从少数类产生合成实例来平衡类别[31]。对于少数类实例的子集，通过搜索得到k个最近邻。将k近邻定义为欧氏距离和mi之间的最小距离，并从中随机选择n个合成实例，记录为Yj,j=1,2,…,n，以创建新的少数实例mnew，如式（6）所述，其中rand是[0，1]之间的随机数。

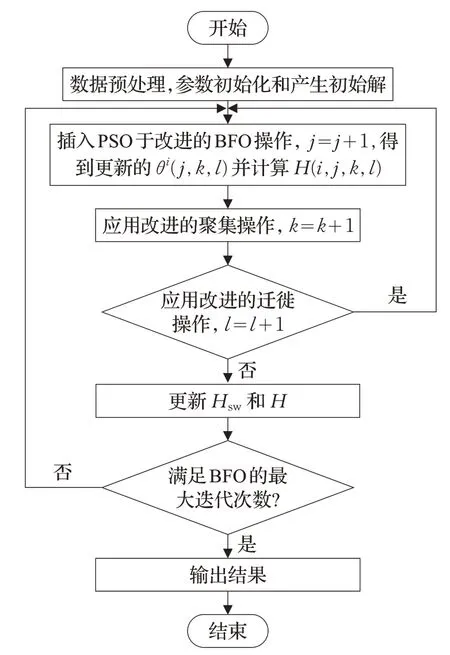
图3 本文算法的流程图

Tomek Link 为一种数据清洗技术，能被有效地应用于消除采样方法中的重叠[32]。Tomek Link 用于删除类之间不必要的重叠，直到属于同一类中最小距离处的最近邻对。假设一对最小欧氏距离的最近邻(mi,mj)属于不同的类，d(mi,mj)表示mi和mj间的欧几里德距离。如果不存在满足式（7）的实例ml,则(mi,mj)为一对Tomek Link。

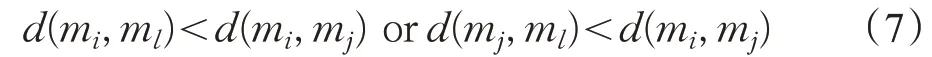
在本文中，用于SMOTE的参数k设置为k=3。在对数据进行预处理之后，产生θi。随后，执行本文算法。针对BFO 算法易陷入局部最优的缺点，本文算法包括改进的趋化操作过程、改进的复制操作过程以及改进的迁徙操作过程。

3.1 改进的趋化操作

原始BFO 算法主要是以趋化操作过程进行搜索。当趋化操作搜索目标区域时，其游动步长和翻滚操作直接影响算法的效果。当游动步长较大时，全局搜索能力较强；反之，则局部搜索能力较强。由于趋化操作的特性，BFO 算法具有良好的局部搜索能力，因为它可以在趋化操作中改变方向，所以局部搜索准确度非常好。但细菌的全局搜索能力只能依靠迁徙操作，其全局搜索能力欠佳。

因为PSO具有较强记忆和全局搜索能力、个体效应和群体效应，本文利用PSO这个优点，将PSO结合到改进的BFO中，可改进原始BFO的趋化操作过程，以便解决原始BFO容易陷入局部优化的问题。通过使用粒子先进行搜索，然后将粒子当成细菌，以提高原始BFO的全局搜索能力。本文目的是找到一个有效的算法，即结合PSO 收敛速度快、搜索能力强和BFO 分类效果佳的优点，提高不平衡数据的准确性。

3.2 改进的复制操作

在原始BFO 算法复制操作过程中，种群规模为S的细菌群中，利用当前细菌位置代价值H作为好坏排列依据，有一半(S/2)的优良细菌被复制，复制产生的子群代替原始细菌群中的另一半劣质细菌，种群的多样性降低。为了增加群体的多样性，并避免丢失最优个体，本文引入父代个体（最优父代个体除外）与最优父代个体做交叉运算。混合公式表示如下：

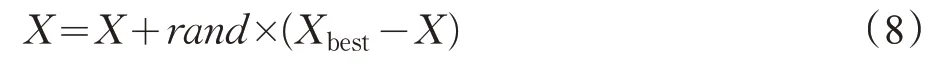
其中，X代表父代个体（最优父代个体除外），Xbest代表最优父代个体，rand为区间[0，1]内的随机数。

3.3 改进的迁徙操作

迁徙操作有助于BFO 算法跳出局部最优解，并找到全局最优解，在原始BFO 的迁徙操作中按照给定的固定概率Ped进行迁徙，没有考虑种群的进化情况。本文改进了原有BFO 算法中的迁徙操作，引入了种群进化因子，根据种群的进化情况进行迁徙，有利于算法寻优的有效性，防止种群进化不前而陷入局部最优。其群体进化因子公式表示如下：

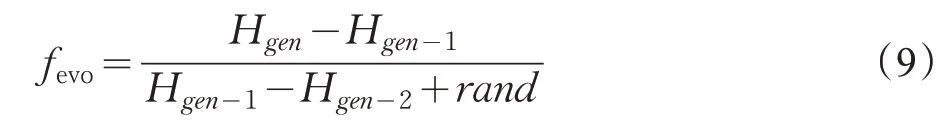
式中，Hgen代表第gen次迭代时的最优代价值，rand用于防止式子中的分母为0，本文用(1-fevo) 代替原始BFO算法中的Ped。当fevo>1 时，则进化加速，此时种群进化程度较快，种群群体处在快而有效的寻优状态，以较低的迁徙概率(1-fevo)进行迁徙，可以保留当前有利的位置信息。当0 ≤fevo<1 时，进化减慢，容易陷入局部最优，需要以较高的迁徙概率(1-fevo)进行迁徙，跳出局部最优解，防止种群进化不前。

为了克服原始BFO 算法容易陷入局部最优的缺点，本文算法的整个过程如下：

（1）设定粒子群种群大小为S，随机生成每个粒子的初始速度和位置，设定PSO 的最大迭代次数为T。在本文中，PSO 插入到每个BFO 的趋化过程中，PSO 的种群大小与BFO相同。设定BFO算法参数Nc,Ns,Nre,Ned,dattract,drepellent,wattract,wrepellent；设定 BFO 迭代次数为Nc×Nre×Ned。

（2）在本文中，代价H定义为计算每个粒子的分类准确度。求出第i个粒子的最优位置，以及总体中所有粒子最优代价时的最优位置。如果和比上一次迭代的值好，则更新和。

（4）如果满足设置的终止条件则停止，否则跳回到步骤（2）。终止条件是达到总体中所有粒子最优代价时的最优位置，或超过设定的PSO 的最大迭代次数T。式（4）和式（5）将粒子视为细菌，PSO完成获得更新的位置。换句话说，在改进的趋化性操作过程中执行PSO以获得更新的位置θi。

（5）执行BFO 群集过程中，由式（3）计算Hsw的代价值。

（6）在改进的复制操作过程中，执行式（8）增加群体的多样性并避免丢失最优个体，即父代个体（最优父代除外）与最优个体做交叉运算。

（7）在改进的迁徙操作过程中，执行式（9）使用群体进化因子fevo。PSO 根据(1-fevo)生成新的θi。在改进的BFO中，用(1-fevo)替换原始BFO中的Ped。

（8）如果满足BFO 的最大迭代次数，则算法结束。最后，在此实验中输出分类准确度的结果。

本文算法中，代价H定义为分类准确度。利用混淆矩阵测试本文算法的性能。混淆矩阵如表3所示。

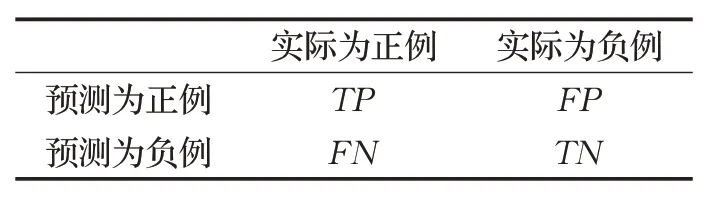
表3 混肴矩阵

TP和FP分别代表真阳性分类和假阳性分类，FN和TN分别代表假阴性分类和真阴性分类。预测值是一个正例，记录为P（Positive）。预测值是一个负例，记录为N（Negative）。预测值与实际值相同，记录为T（True）。预测值与实际值相反，记录为F（False）。模型分类后，在数据集中定义的结果有4 个：TP,预测为正，实际为正；FP,预测为正，实际为负；TN,预测为负，实际为负；FN,预测为负，实际为正。分类准确度计算公式如下：

采用接受者操作特征曲线（Receiver Operating Characteristic，ROC）和曲线下面积（Area Under the Curve，AUC）可以测试分类结果的性能。这是因为ROC 曲线具有良好的特性：当测试数据集中正例和负例的分布发生变化时，ROC 曲线可以保持不变。不平衡数据常发生在实际数据集中，也就是说，负实例要比正实例多得多（反之亦然），并且测试数据中正实例和负实例的分布可能随时间变化。计算AUC可作为不平衡数据的评估方法，它可以全面描述分类器在不同决策阈值下的性能。AUC的计算公式如下：

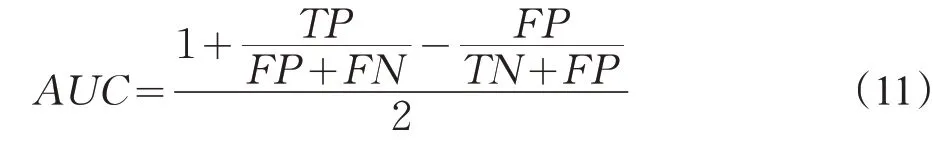
4 实验结果和分析

本文目的是为了获得有效的算法来提高不平衡数据的准确性。为了验证本文算法的性能，利用卵巢癌微阵列数据、垃圾电子邮件数据集和动物园数据集进行仿真实验，数据预处理采用Borderline-SMOTE 和Tomek Link的方法。

4.1 参数取值和实验结果收敛性及运算复杂度分析

算法的参数值设定是算法性能和效率的关键，BFO有许多参数，如何确定BFO 的最优参数来优化算法性能是一个非常复杂的问题。原始BFO参数取值对实验结果收敛性及运算速度的影响主要有：

（1）种群规模S的大小影响BFO效能的发挥，种群规模小，BFO的计算速度快，但种群的多样性降低，影响算法的优化性能；种群规模大，个体初始时分布的区域多，靠近最优解的机会就越高。也可以说是，种群规模越大，种群中个体的多样性就越高，越能避免算法陷入局部最优值。但是种群规模太大时，算法的计算量就会增加，算法的收敛速度会变慢。

（2）趋向性操作执行的次数Nc的值越大，算法的搜索更细致，但是算法的复杂度也会随之增加；反之，Nc的值越小，算法更容易陷入局部最优值，算法的性能好坏就更多地依赖于复制操作。

（3）复制操作执行的次数Nre的值越大，算法越能避开食物缺乏或者有毒的区域而去食物丰富的区域搜索，从而提高算法的收敛速度。当然Nre太大，同样也会增加算法的复杂度；反之，如果Nre太小，算法易早熟收敛。

（4）迁徙操作执行的次数Ned值太小，算法没有发挥迁徙操作的随机搜索作用；反之，Ned值越大，算法能搜索的区域越大，解的多样性增加，能避免算法陷入早熟，其算法的复杂度也会随之增加。迁徙概率Ped选取适当的值能帮助算法跳出局部最优值，但是Ped的值不能太大，否则BFO就变成了随机搜索算法。

启发式搜索算法的自身优势，一次运行就得到一组解，能够耗费较小时间和计算代价搜索到理想的解，并取得很好的效果。其中，粒子群优化算法由于其收敛速度快、搜索能力强的优点受到诸多研究者关注。本文利用PSO的优点，将PSO结合到改进的BFO中，可改进原始BFO 的趋化操作过程，解决原始BFO 容易陷入局部优化的问题。为了避免出现大量计算时间又可找到全局解，本文在设定PSO和BFO的参数时，依据经验值将BFO算法参数设置为S=50,Nc=100,Ns=4,Nre=4，Ned=2,Ped=0.25,dattract=0.05,drepellent=0.05,wattract=0.05,wrepellent=0.05,α(i)=0.1,i=1,2,…,S。BFO 迭代次数为Nc×Nre×Ned=100×4×2=800[25]。PSO 的最大迭代次数设置为5 000，其他参数设置为惯性权重w=0.6，学习因子c1=c2=1.5，每个粒子的最大速度vmax=2[24]。本文采用随机分区的10 倍交叉验证结果，即将数据分为10 份，其中9 份数据作为训练数据，剩下1份作为测试数据。

4.2 本文算法与其他算法的分类准确度比较分析

下面除了研究本文算法外，也用其他现有算法进行比较，如支持向量机（Support Vector Machine，SVM）、决策树（DT）、随机森林（Random Forest，RF）、K-最近邻算法(KNN)及原细菌觅食优化（BFO）。支持向量机是在高维特征空间中使用线性函数假设空间的学习系统。决策树使用分区信息熵最小化递归地将数据集划分为更小的子分区，然后生成树结构。随机森林是一种集成的分类学习方法，它在训练时构造多个决策树，并输出依赖于大多数类的类。K-最近邻算法是一种基于n维模式空间中最接近训练样本的目标分类方法。原细菌觅食优化算法如第2.1节所述。

（1）表4 分别列出了卵巢癌微阵列数据、垃圾电子邮件数据集和动物园数据集的分类性能。从表4 中可以看出，本文算法对卵巢癌微阵列数据、垃圾电子邮件数据集和动物园数据集的平均分类准确度分别为93.47%、96.42%和99.54%。从表4 可以明显看出，在对所有方法进行比较后，本文算法具有最优的分类结果，这是因为智能信息可以在测试数据集的分类上有好的性能表现，而本文算法也具有类似的功能，因此在分类准确度上有较好的表现结果。

（2）在比较结果中，可以发现原始BFO对三个数据集的分类准确度均没有本文算法分类准确度好。因为原始BFO 可以在趋化操作中改变方向，所以局部搜索能力更好，但是全局搜索只能依靠迁徙操作过程，全局搜索能力不是很好，所以在分类准确度表现上没有本文算法好。

（3）本文算法在改进的趋化过程中引入了PSO，具有记忆和全局搜索的能力。在研究中首先使用粒子进行全局搜索，然后将这些粒子视为细菌，提高了全局搜索能力。改进的复制操作过程中，在保留最优个体的情况下，对复制后的父代引入交叉算子，增加种群的多样性。在改进的迁徙操作过程中，引入了(1-fevo)替换原始BFO 中的Ped，以防止种群死亡和陷入局部最优状态，因此在分类准确度上有较好的表现。

表4 不同算法的分类准确度

4.3 ROC和AUC分析

在本次的仿真实验中，ROC 和AUC 用于评估本文算法性能，AUC的值介于0～1之间且越大越好。卵巢癌微阵列数据的AUC 值为0.979，如图4 所示。垃圾电子邮件数据集的AUC 值为0.987，如图5 所示。动物园数据集的AUC值为0.995，如图6所示。实验结果显示，本文算法具有良好的分类性能。

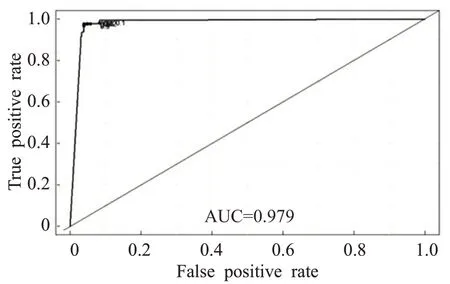
图4 卵巢癌微阵列数据的ROC和AUC

图5 垃圾电子邮件数据集的ROC和AUC

图6 动物园数据集的ROC和AUC

本文提出了混合粒子群和改进的细菌觅食优化算法应用于不平衡数据的分类，根据研究结果，提出以下几方面的建议：

（1）算法运行的改进。实现优化的关键是算法的操作，设计出色的运算对提高算法的性能和效率起着重要作用。在原BFO算法中，提高其趋化性和复制性，迁徙操作，协调处理算法的局部挖掘能力和全局探索能力将成为BFO研究的热点。

（2）算法参数的选择。算法的参数值是决定算法性能和效率的关键。在进化算法中，没有通用的方法来确定算法的最优参数，其中大多数是根据经验选择的。目前，BFO的参数很多，如何确定BFO的最优参数来优化算法本身的性能是一个非常复杂的问题。本文在4.1节中进行了参数取值和实验结果收敛性及运算复杂度的分析，可作为未来继续研究的方向。

（3）与其他算法结合。结合BFO 和其他算法的优点以提出更有效的算法是BFO研究中的重要课题。

5 结论

本文提出一种混合粒子群和改进的细菌觅食优化算法应用于不平衡数据的分类。数据预处理用Borderline-SMOTE和Tomek Link技术。随后，将本文算法应用于不平衡数据的分类，以解决原始BFO 算法陷入局部最优的缺点。使用三个数据集来测试本文算法的性能。本文算法包括改进的趋化操作过程、改进的复制操作过程以及改进的迁徙操作过程。在本文中，通过在改进的趋化操作过程中使用粒子进行搜索，然后将粒子视为细菌，可以提高BFO 的全局搜索能力。在改进了趋化操作之后，进行了群集操作、改进的复制操作，最后进行改进的迁徙操作。本文算法对卵巢癌微阵列数据的平均分类准确度为93.47%，对垃圾电子邮件数据集和动物园数据集的平均分类准确度分别为96.42%和99.54%，卵巢癌微阵列数据的AUC值为0.979，垃圾电子邮件数据集和动物园数据集的AUC 值分别为0.987 和0.995。实验结果表明，本文算法与现有方法比较，在不平衡数据分类准确度中有良好的表现结果。