考虑决策者权重和核心评级的模糊排序方法

郭皓月，樊重俊

上海理工大学 管理学院，上海 200093

1 引言

决策问题的关键是从备选方案中选择一种目标最优化的方案，及时性和科学性是高质量决策的核心。通常情况下，现实决策问题的评价对象具有复杂性，决策者的偏好具有差异性，决策者的思维具有模糊性，评价语言具有不确定性，这类决策问题称之为模糊多属性决策（Fuzzy Multiple Attribute Decision-making，FMAD）。传统的决策方法很难依据决策者的模糊评价语言给出合理的方案排序，进而增加了最终方案选择的困难。因此，研究模糊多属性决策问题对提升组织与企业的生产、运营、管理的效率有着重要意义。

模糊集（Fuzzy Set）率先由美国控制论学者Zadeh于1965 年提出，这是一种十分符合客观实际且应用广泛的描述方法，其核心是引入隶属度概念以描述“是”与“非”的中间状态，突破传统决策中“非此即彼”的桎梏[1]。1976年，Fuzzy Set引入我国后，发展十分迅速，已在决策科学等众多领域发挥重要作用。FMAD 一直是模糊集理论（Fuzzy Set Theory，FST）的热门课题之一，也是贴近真实评价、极具挑战性的研究热点。国内外研究一方面集中在模糊评价语言的量化处理上，Herrera和Martinez 等提出了关于语言信息集结的二元语义分析方法[2-4]。徐泽水等[5]给出了一种将决策者的定性语义判断转化为定量权重信息的决策支持方法，这大大降低了决策者的工作量。蒋绍忠[6]通过集结不同专家综合意见，丰富了模糊多属性决策的赋权理论。

另一方面，针对多属性决策（Multi-Attribute Decisionmaking，MAD）方法的改进，也备受国内外学者的关注。李存斌等[7]将前景理论引入模糊数；李超群等[8]构建了方案与正负理想解的犹豫模糊“垂面”之间的距离公式，从而克服了传统TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）评价某一方案同时接近正负理想解的局限；宝斯琴塔娜和齐二石[9]在有序模糊数[10-11]的基础上，增加了一个方向属性，提出了灰色关联的TOPSIS 优选算法，使具有歧义语言的标度更加清晰，并减少信息损失。孙世岩和朱惠民[12]在改进 PROMETHEEII（Preference Ranking Organization Method for Enrichment Evaluations）的基础上，通过分析参数的鲁棒性配置优选函数的参数。另外，一些新的FMAD方法被相继提出。杨威等[13]在方案排序前，运用TOPSIS 给出各评价专家权重，这克服了决策者自身知识结构的不完备。曾三云和龙君[14]在已知属性优先序的情况下，通过期望值算子得到各方案量化后的期望效用值，并在此基础上对备选方案进行排序。Yatsalo等[15]在模糊环境下提出了一种新的MAD 方法用以方案排序，此方法给出了模糊可接受性分析（Fuzzy Rank Acceptability Analysis，FRAA），进一步研究并修正了模糊算法中过估计的问题。

综上，多属性决策的不确定性一般不能完全由统计概率模型处理，这也是增加MAD 复杂性的主要原因之一。诸如 AHP（Analytic Hierarchy Process）[16]、MAVT（Multi-Attribute Value Theory）[17]、MAUT（Multi-Attribute Utility Theory）[18]之类的传统决策方法依赖于决策者的主观判断，而现有的MAD 方法没有考虑语言评价的模糊性与偏好的差异性，如TOPSIS[13]和PROMETHEE[12]等。鲜有国内外模糊多属性决策研究，综合考虑决策者和评价对象属性权重对方案排序的影响。对此，本文针对模糊多属性决策问题，在设计决策者权重迭代算法和评价对象属性权重确定方法的基础上，结合模糊理论与积分式偏好函数，构造积分式模糊排序方法，同时通过算例分析和决策结果的对比，以期证明该方法的一致性、可行性、有效性及优越性。

2 模糊理论及定义

相对于数学上的集合来说，现实评价对象不能简单用“属于”“不属于”某个集合来描述元素与模糊集的关系，而是通过反映某元素隶属于模糊集合的程度来衡量，即隶属度。隶属度函数的值在闭区间[0，1]内取任意值，其值越接近于1表示隶属度越大，取值为0表示元素不属于模糊集合，取值为1表示元素属于模糊集合。

2.1 模糊集及隶属函数

定义1 给定论域X，从X到单位区间[0，1]的映射，称为X上的模糊集，记作A，映射称为模糊集A的隶属函数，μA(x)表示x∈X属于模糊集的程度。

由定义1可以看出，模糊集A由元素和对应的隶属度两部分组成，可表示为A={(x,μA(x)):x∈X}，所有模糊集组成的集合，记为F。在现实情形中，A表示评价对象，如属性、方案等。常见的模糊集有区间数、三角模糊数、梯形模糊数、语言变量等[6]，其中三角模糊数的应用较为广泛。令三角模糊数为，其隶属度表达式为：

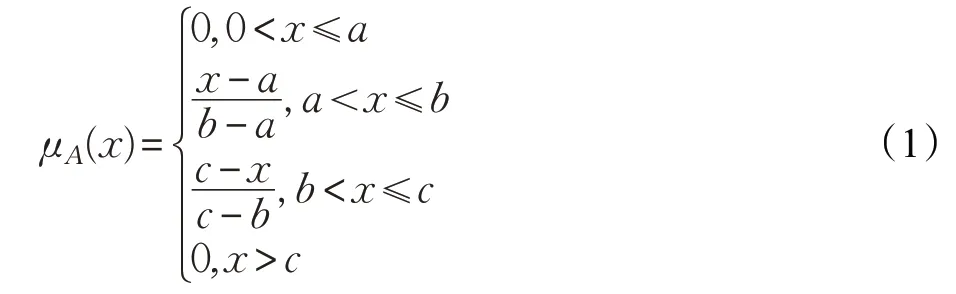
其中，0＜a ＜b ＜c,a称为的评级下限，c称为的评级上限，b称为的核心评级。

2.2 模糊截集

定义2 若A∈F,α∈[0,1],A的α截集为Aα={x∈X|μA(x)≥α}。不同水平的α对应x的下、上边界分别记为Uα、Vα，模糊集A也可以表示为：

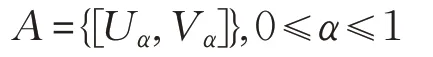
由定义1和定义2，三角模糊数α截集如图1所示。

2.3 模糊距离

定义3 若二者间的距离记为Aij，则：

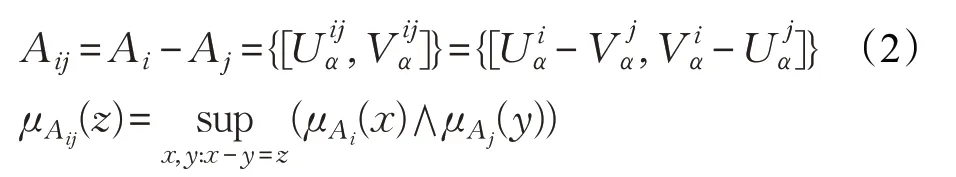
其中，x,y,z∈X，代表关于对象的评价。

图1 三角模糊数α 截集

本文记d+(Aij)、d-(Aij)分别表示由α和Aij围成区域的正向面积和负向面积[19]，如下：

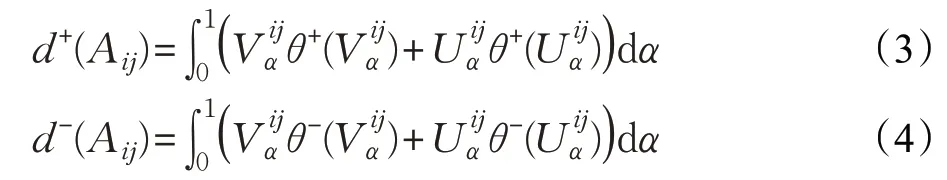
其中，θ+(y)、θ-(y)均为是阶跃函数，有。由α和Aij围成区域的总面积d(Aij)可表示：

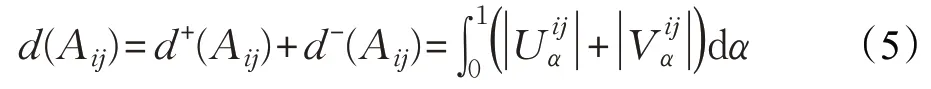
2.4 模糊关系

定义4是模糊直积空间F×F下的模糊关系，表达式为：

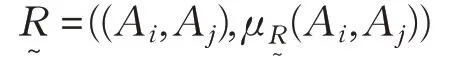
基于定义3、定义4，对于模糊直积空间F×F中的积分式模糊关系，若有d(Aij)＞0，本文定义积分式模糊偏好函数如下：

根据任意两个评价对象间的偏好度，比较二者间的优劣。对任意Ai,Aj∈F，有：

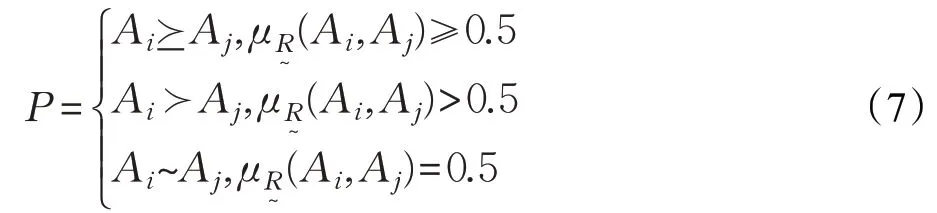
3 IFRM设计

3.1 模糊评价量化

自然语言评价是生活中常用的模糊评价方式，包含决策者偏好中固有的主观性。日常生活中，人们常用“很好”、“一般”和“差不多”等这些模棱两可的语言变量展开评价，甚至做决策，这显然是不科学的。对此，可运用模糊评级的方法将语言变量转变为模糊数。本文选取1-3-5-7-9评价等级，将属性或方案评价的语言变量转换为对应的三角模糊数评级[20]，如表1。

表1 语言变量对应的模糊评级

把语言变量转化为模糊评级后，运用隶属度函数，求得包含模糊评价信息的三角模糊数，进而为备选方案排序奠定基础。本文选取三角模糊数的隶属度函数如图2所示。

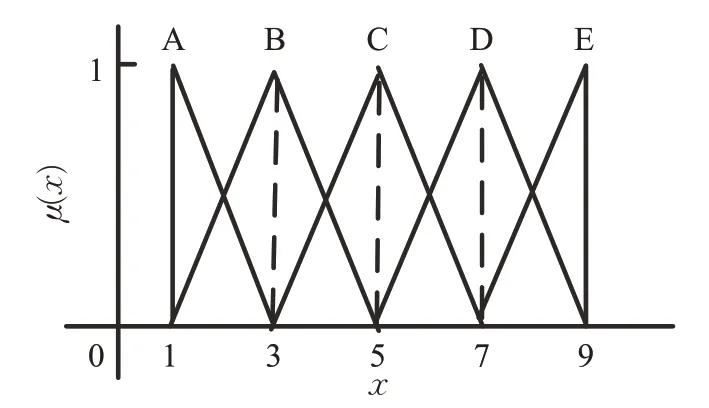
图2 各评级隶属度函数

3.2 综合集结模糊评级的确定

本文将模糊的语言评价转化为三角模糊数，进而求得代表备选方案的综合集结模糊评级，具体步骤如下：

步骤1 方案集和评价属性的确定。

假设评价对象有n个备选方案、m个评价属性、h名决策者，决策者来自p个群体，且p≤h，方案集S、属性集Y、决策者集D及群体集O分别表示为：

令gk(k=1,2,…,h)表示第k个决策者的权重，由步骤4 中的决策者权重调整算法确定。第j个属性对应的权重为wj(j=1,2,…,m)，并由步骤5中的熵权法计算给出。

步骤2 模糊决策矩阵的构建。

第k位决策者Dk对第i个方案Si(i=1,2,…,n)关于第j个属性Yj的评价为（自然语言评价），转化为三角模糊数，模糊数评价矩阵为，简称评价矩阵。所有决策者的三角模糊数评级上、下限对应的最大、最小值，代表集结模糊评级的上、下界限。在决策者权重下，所有决策者核心评级的加权累加值，表示集结模糊评级的核心评级。这样集结模糊评级能考虑所有决策者的观点和倾向，其中核心评级是关键。则第i个方案的第j个属性的集结模糊评级表示为：

在此基础上，构建方案集S与属性集Y的模糊决策矩阵，简称决策矩阵：

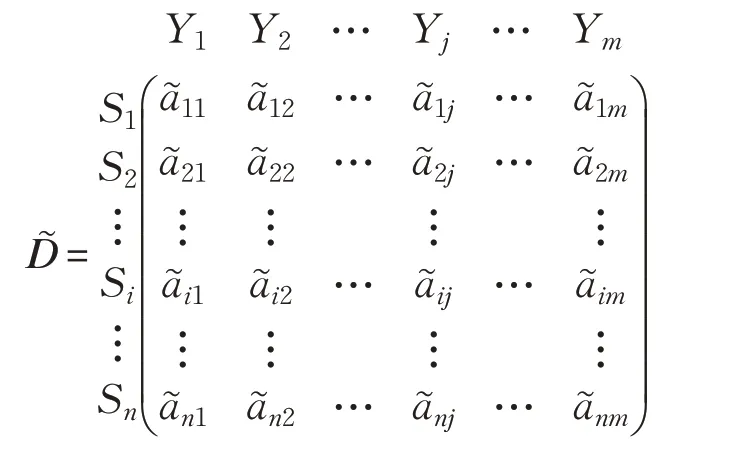
步骤3 评价矩阵和决策矩阵的规范化。

若对应的Yj为正向指标（或效益型指标），=，其中；若对应的Yj为负向指标（或成本型指标），，其中=min{aij,bij,cij}。同理，按照上述方式规范化为。

步骤4 决策者权重调整。

为了决策的科学性，决策者通常来自不同的群体，他们在知识背景、个人偏好等方面均存在着显著差异。这也使得在决策过程中，决策者的评价有不同的权重，如行业专家的评价更具参考价值，其权重相对较大。

（1）初始群体权重与个体权重

根据决策中所属群体和决策问题的特点，运用AHP给出p个群体的主观权重 (λ1,λ2,…,λq,…,λp)。各决策者的初始权重等于所属群体的权重平均值，例如若决策者Dk属于群体Oq,评价的权重为λq/card(Oq)。令G0=为决策者的初始权重。进一步，由步骤2、步骤3给出G0下的规范化评价矩阵和决策矩阵。

（2）权重调整规则

在初始权重G0下，评价矩阵偏离决策矩阵越大，评价可参考的价值越小，权重的调整幅度θ也越小。第k位决策者的第τ次权重调整规则如下：

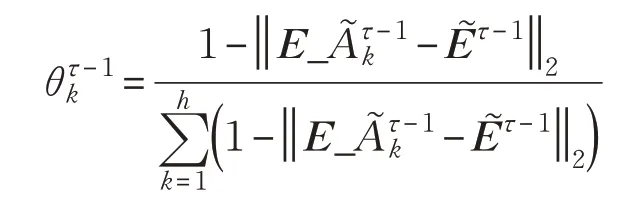
其中，τ表示决策者权重迭代的次数，‖ ‖2表示欧式距离，分别代表第τ-1 次迭代中决策者k的规范化评价矩阵与决策矩阵。

个体评价矩阵和决策矩阵间的偏离度可近似由二者核心评价标度间的偏离度衡量，如下：

（3）权重调整终止条件

判断相邻迭代的决策者权重相差不大于某个足够小的常数ε时，即，权重调整终止，Gτ作为决策者的稳定权重，并计算出转入步骤5。否则，继续迭代，τ的计数加1。

步骤5 决策属性权重的确定。

（1）计算属性Yj的信息熵

其中，φ是系数，且表示取三角模糊数的核心评价标度。

（2）确定属性的权重

在求得第j个属性信息熵ej的基础上，计算第j个属性的权重wj，如下：

其中，lj表示属性集中第j个属性信息熵的冗余，有：

步骤6 计算加权规范化决策矩阵。

基于已求得的评价属性权重wj，计算加权规范化决策矩阵：

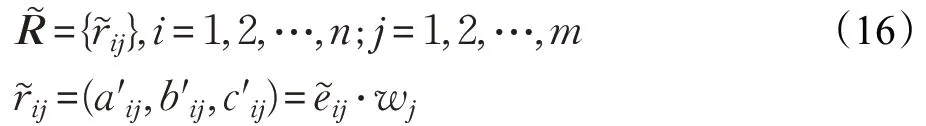
其中，“·”表示广义乘子。

步骤7 综合集结模糊评级。

整体考虑各属性的模糊评价，形成方案Si的综合集结模糊评级：

其中，ai=min{a′ij}，ci=max{c′ij}。

3.3 模糊集的排序

在决策理论中，模糊排序描述更符合人们的直觉，模糊排序置信度能够给出该直觉的概率。

（1）模糊排序表示

模糊排序表示（Fuzzy Rank Expression，FRE）即通过符号表达式说明备选方案排序的规则。令{A1,A2,…,Ai,…,An}⊂F是模糊集一个有限集。本文定义模糊排序描述为：

Tit=(Ai,t)={Ai排在第t位 },i,t=1,2,…,n

对于Tit，在模糊集集合{A1,A2,…,Ai,…,An}中存在t-1 个模糊集排在Ai的前面，n-t个模糊集排在Ai的后面。备选方案选取原则为：

在相对偏好μR～(Ai,Aj),i,j∈{1,2,…,n}下，Tik∈F×Nn(Nn={1,2,…,n})的表达式如下：

若模糊集Ai排在第一位：

若模糊集Ai排在第二位：

若模糊集i排在第t位：

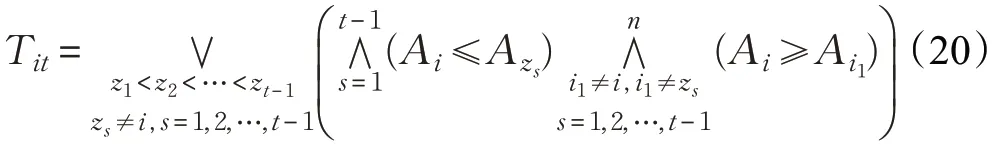
若模糊集Ai排在末位：

其中，(∨)、(∧)分别表示取大和取小的广义模糊算子。

（2）模糊排序置信度

令B(i,t)表示模糊集Ai排在第t位的置信度，称作模糊排序置信度（Degree of Fuzzy Rank Confidence，DFRC）或模糊排序的可接受度指数。某个模糊排序表示Tit，其对应的排序可接受度计算规则如下：

模糊集i排在第一位的置信度为：

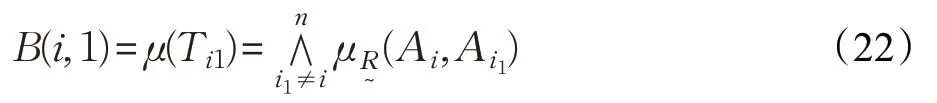
模糊集i排在第二位的置信度为：

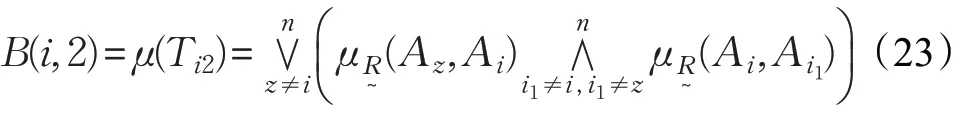
模糊集i排在第t位的置信度为：

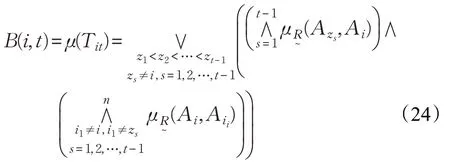
模糊集i排在末位的置信度为：

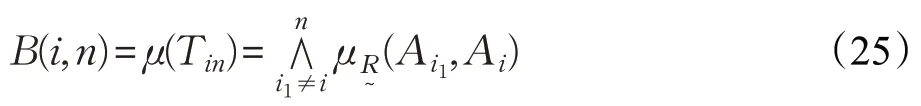
模糊排序置信度（DFRC）在理论上进一步验证了模糊排序表示（FRE）的可行性。从概率角度来看，式（22）～（25）分别表示式（18）～（21）模糊排序出现的可能性大小。显然，可将各备选方案看成模糊集，备选方案最佳的模糊排序Tit是最大化排序置信度，即。

3.4 IFRM流程

本文针对模糊多属性决策问题，首先将多个决策者的评价语言转化为三角模糊数。然后采用AHP主观给出各群体和决策者初始权重，并基于个体评价矩阵和决策矩阵间的差距，更新决策者权重。在最终迭代的规范化决策矩阵基础上，运用熵权法计算出方案各属性权重，进而求出加权规范化决策矩阵和各方案对应的综合集结模糊评级。最后通过积分式模糊偏好函数，求出置信度最大的方案排序。这个过程称为积分式模糊排序方法（Integral Fuzzy Ranking Method，IFRM），它是一种改进了的模糊方案排序方法。IFRM流程如图3。

步骤1 输入方案集S、属性集Y、群体集O、常数ε∈[0,1]及所有决策者对每个方案对应属性的模糊语言评价，并令最佳方案排序的位序为pos=1，决策者权重计算迭代次数τ=0。

步骤2 运用AHP 确定p个群体的主观权重，在此基础上，计算决策者初始权重G0。依据表1 将模糊评价转化为三角模糊数，形成评价矩阵。然后运用式（8）整合出第i个方案第j个属性的集结模糊评级，并形成原始决策矩阵。接着通过式（9），给出对应的规范化评价矩阵和决策矩阵。

步骤3τ=τ+1，按照式（10）和（11）更新第τ代所有决策者的权重Gτ，参照式（8）和（9）记录规范化决策矩阵。

步骤4 判断个体权重更新是否满足终止条件。若，导出并转入步骤 5；否则转入步骤3。

步骤5 取中每个三角模糊数的核心评价标度，代替对不同方案属性的评价。在此基础上运用熵权法（式（12）～（15））确定第j个评价属性的权重wj，进而通过式（16）和（17）分别计算加权标准化模糊决策矩阵、第i个备选方案的综合集结模糊评级。

步骤6 判断是否仍有备选方案未被排序，即pos≤n?若是，转到步骤7；否则转到步骤10。

步骤7 基于积分式模糊偏好（式（2）～（6））和方案i排在第pos序位的概率计算规则（式（22）～（25）），给出各方案排在第pos序位的置信度，然后选择对应置信度最大的方案s*作为最佳方案，并将方案s*和置信度分别记录在数组Choice_s和Choice_B中。

图3 IFRM流程图

步骤8 更新待排序的备选方案集。从原方案集S中剔除已排序的方案s*作为新的方案集，即S=S-s*。

步骤9 最佳方案排序的位序pos向前移动一位，即pos=pos+1。然后，返回步骤6。

步骤10 输出数组Choice_s和Choice_B，结束算法。

从中可以分析出，AHP确定群体初始权重的时间复杂度为O(p2)。决策者权重更新算法的迭代次数与终止条件ε和决策者规模h有关，式（10）执行的次数记为f(h,ε)。ε取值越小，该算法的时间复杂度越大，记为O(f(h,ε))，本文ε取0.05。基于积分式模糊偏好，对备选方案两两对比过程的时间复杂度为O(n2)。因此，针对模糊多属性决策问题，IFRM 综合考虑了决策者评价和评价对象属性间的差异，并给出了最佳决策的置信度，算法的复杂度为max{O(p2),O(f(h,ε)),O(n2)}。

4 算例分析

4.1 问题描述

共享单车作为环保、共享经济的代表性产业之一，不仅符合“绿色交通”“低碳出行”的生活理念，而且以其便捷、低廉等特性进一步解决了出行“最后一公里问题”。2015年以市场为主导的共享单车逐渐走入人们的生活，并为广大的城市居民所接受，成为其青睐的出行方式。但是市场上各种品牌的共享单车繁多，目前用户量较大的4 种品牌共享单车：A 品牌单车S1、B 品牌单车S2、C品牌单车S3和D品牌单车S4，它们各有侧重、各有优势。例如A比较安全，置物能力强；B外观漂亮；C用车押金较少，舒适度高；D用车单价低。居民在选择何种品牌共享单车上往往“不知所措”。本文从共享单车8个属性：舒适度Y1、置物能力Y2、客服质量Y3、安全性Y4、美观度Y5、找车难度Y6、用车押金Y7、用车单价Y8，其中Y1～Y5为正向指标，Y6～Y8为负向指标，设计调查问卷，以期收集用户的模糊语言评价，进而运用IFRM方法给出4 种共享单车的居民倾向排序。同时，与其他MAD 方法排序结果对比，以期验证IFRM 方法的可行性、有效性和优越性。

4.2 方案优先度

第k位决策者对每个方案Si(i=1,2,3,4)关于属性Yj(j=1,2,…,8)的语言评价为x~ijk，并将其量化为S与Y的决策矩阵，如表2所示。依据不同方案不同属性对应的三角模糊数的核心评价标度，运用熵权法求出8个属性权重如表2，其中居民最看重用车押金，其次是安全性、舒适性、用车单价和找车难度，它们的权重均超过0.1。在共享单车领域，时常出现押金难退还的现象，导致决策者对骑车押金较为敏感。

表2中的模糊决策矩阵规范化后，与属性权重做广义乘法，得到加权标准化决策矩阵，如表3 所示。该矩阵从整体上考虑了不同性质的属性对最终模糊评价的影响。表3中含有各方案对应的综合集结三角模糊数a~i。

表2 共享单车方案与属性的决策矩阵及属性权重

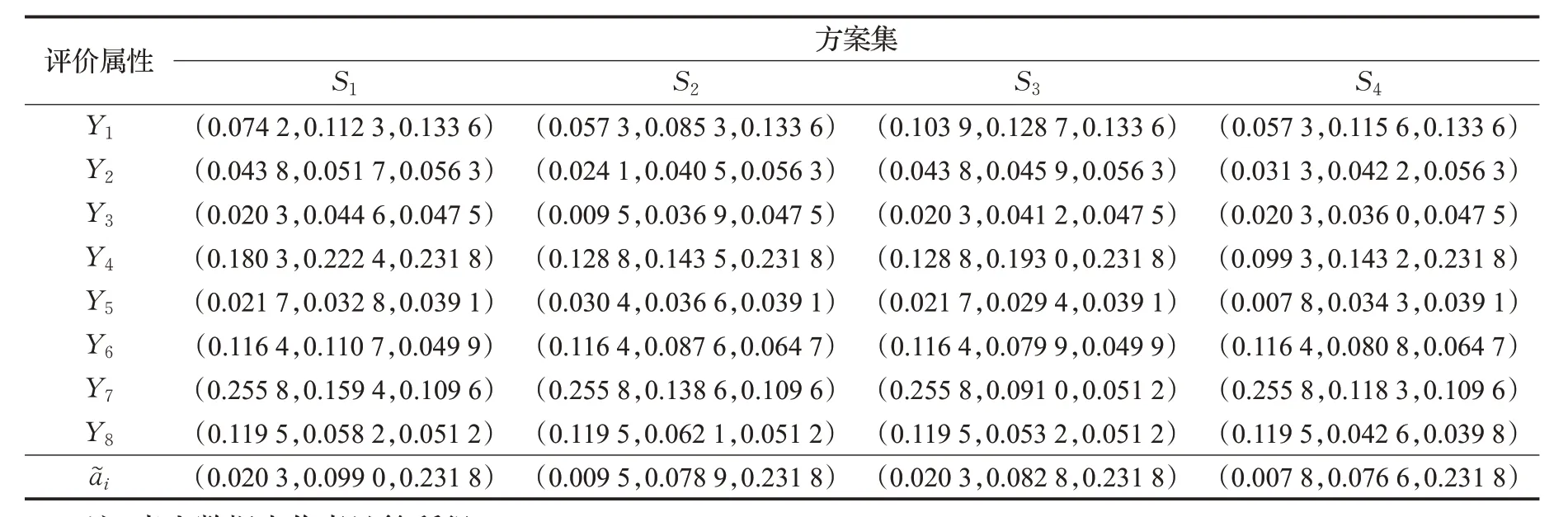
表3 共享单车方案综合集结模糊评价

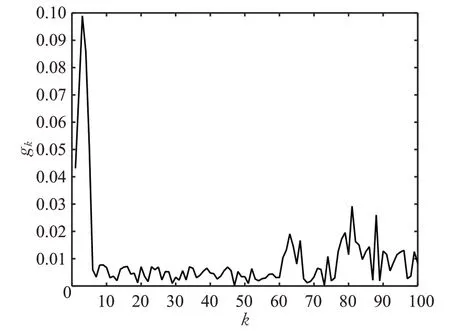
图4 决策者稳定权重

运用积分式模糊偏好函数，计算任意两个方案间的模糊优先度，得到方案间模糊偏好矩阵如表4，主对角线的元素均为0.5，对称两元素之和为1。

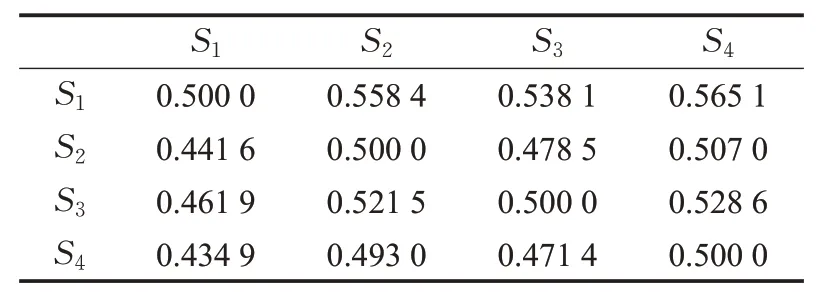
表4 方案间模糊相对偏好

4.3 排序结果及对比分析

在表4的基础上，本文通过IFRM的步骤6～10，求出各个序位上的最佳方案及对应的置信度，并对比AHP[16]、MAVT[17]、MAUT[18]、TOPSIS[13]、PROMETHEE[12]和 FMAA[15]下的方案最终排序，如表5。基于IFRM的最终排序：方案1—方案3—方案2—方案4，建议市民首选A 品牌单车，其次 C 品牌，然后B 品牌，最后 D 品牌单车，该种方案下总置信度为2.0807，且每个方案排序对应的置信度均大于0.5。

表5 IFRM和其他MAD方法求得的排序结果对比

层次分析法（AHP）是依据决策思维的分解、判断、综合等特点，将待评价对象的属性分成不同层次的主观决策方法；多属性价值理论（MAVT）和多属性效用理论（MAUT）分别是基于价值函数与效用函数值确定指标权重，进而综合排序的决策方法，这两种函数均建立在决策者的偏好结构之上。这三种方法均依赖于决策者的主观，所求得的最终排序结果与IFRM的排序一致。

逼近理想解排序法（TOPSIS）通过量化备选方案与最优、最劣方案的距离进行排序；偏好顺序结构评估法（PROMETHEE）在保证评价信息完整的基础上，运用优先函数依次比较两种方案的优先度；模糊多准则可接受性分析（Fuzzy Multicriteria Acceptability Analysis，FMAA）采用模糊理论对备选方案排序，并分析每种排序的可接受性。PROMETHEE、TOPSIS 与 IFRM 的排序相近，只是方案3 和方案4 调换了位置。FMAA 的排序结果与IFRM完全一样。

进一步说明，对于模糊多属性决策问题，IFRM的计算结果与其他MAD 方法的排序具有高度一致性，且有较高的可信度。相对而言，IFRM 的时间复杂度尽管有所增加，但仍为多项式阶时间复杂度。IFRM 以时间复杂度为代价，不仅考虑了决策者评价的参考价值，而且将评价对象属性的重要程度融入备选方案排序中，还量化了方案最佳排序的置信度，更贴合实际决策情境。因此，本文提出的IFRM对模糊多属性决策问题具有一定的可行性、有效性和优越性。

5 结束语

评价语言的不确定性增加了多属性决策问题的难度，本文从模糊理论出发，考虑决策者权重，并由属性核心评级确定属性对评价的影响程度，设计了积分式模糊排序法（IFRM）。首先，将多属性模糊评价语言量化为三角模糊数评级，并把三维评级拆分为评级下限、核心评级和评级上限。然后，采用AHP 给出各决策群体的权重和个体的初始权重，根据个体评价矩阵和决策矩阵的偏差，不断更新个体权重。接着，对于迭代后的规范化决策矩阵，运用熵权法给出评价属性的权重，进而形成代表各个备选方案的综合集结模糊评级。随后，通过积分式模糊偏好函数，给出最佳方案排序及每个序位方案对应的置信度。最后，以居民出行选择共享单车实际问题为例，运用IFRM计算出4种备选单车的排序，并与常见多属性决策方法的结果对比，进一步说明了IFRM的可行性、有效性和优越性。但IFRM仅依据核心评级确定属性权重，没有充分运用语言评价信息，存在一定局限性，这也是后续研究需要改进的地方。