时间序列趋势相似性度量方法研究

谭章禄，王兆刚，胡 翰

中国矿业大学（北京）管理学院，北京 100083

1 引言

相似性度量是数据挖掘的基础，针对时间序列数据的相似性度量已经成为时间序列数据挖掘的研究热点之一[1-2]。其中，欧氏距离和动态时间弯曲（Dynamic Time Warping，DTW）是目前使用较多的时间序列相似性度量方法。但欧式距离只能处理等长度的时间序列，且无法识别变化趋势，而动态时间弯曲距离虽然较好地克服了欧式距离的不足，但是计算复杂，时间复杂度较高，限制了其应用范围[3]。

基于时间序列模式化的相似性度量方法，为时间序列的趋势相似性度量提供了新的思路和可能，并取得了较多成果。

张海涛等[3]在以分段聚合近似实现数据降维的条件下，根据分段子序列的变化方向进行趋势符号化，然后提出用于时间序列相似性度量的SMVT（Similarity Measurement of Variation-Trends）方法。刘慧婷等[4]通过经验模态分解（Empirical Mode Decomposition，EMD）提取趋势信息，分段后基于上升、保持、下降三种变化趋势实现模式化转化。肖瑞等[5]提出了基于时间序列变化趋势的相似性度量方法和聚类方法，其中基于趋势的相似性度量方法首先对时间序列进行区间划分和区间内的趋势形态判断，生成短的趋势符号序列，然后计算各趋势符号的一阶连接性指数，最后通过计算两序列中各趋势符号一阶连接性指数的塔尼莫特系数完成相似性度量。王钊等[6]以上升、保持、下降的涨落模式保存原序列的趋势变化信息，利用最长公共子序列算法计算涨落模式序列之间的形态相似性。基于局部变化方向实现序列的趋势转化，虽然可以有效描述短期趋势，但其有序组合无法准确反映时间序列的长期变化方向，难以保留时间序列的整体趋势信息，从而影响后续趋势相似性的度量效果。

王达等[7]基于分段线性表示方法实现子序列划分，在三元模式化的基础上，提出模式距离概念，用以度量时间序列变化趋势的相似性。董晓莉等[8]依据分段线性表示实现分段化处理，依据7种变化趋势实现模式化转化，提出基于形态的相似性度量方法。李正欣等[9-10]以拟合线段的倾斜角和时间跨度作为模式的描述方式，提出一种基于动态时间弯曲（DTW）的多元时间序列趋势距离匹配方法，以斜率距离与时间跨度差距的线性综合度量模式之间的差异。李海林等[11]基于SAX（Symbolic Aggregate Approximation）的均值符号化距离与分段导数序列DTW 距离的线性综合，将动态时间弯曲与符号距离相结合来度量时间序列间的数值差异与形态差异距离。上述的趋势相似性度量方法，均遵循“模式差异大，则数字距离大”的原则，但模式化的时间序列实际上是原始数据经过离散化处理后的一种符号化数据，尤其是上升、保持、下降等趋势形态之间的差异应该是对等的，即上升与下降之间的距离和上升与保持之间的距离是一样的，都是两种不同的变化趋势，而不是前者大于后者，统计距离难以准确度量衡量序列变化方向的差异，会在一定程度上影响趋势相似性度量的准确性。

王燕等[12]在基于关键点实现时间序列分段的基础上，对分段均值和斜率的符号化序列进行算术编码，提出基于均值编码距离和斜率编码距离的分层欧氏距离的相似性度量方法，综合考虑序列的统计距离和形态距离，达到序列整体趋势匹配以及细节拟合的目标。一方面，分段均值无法反映局部形态，基于均值编码距离实际上是数值差异，无法识别趋势差异，其筛选结果会限制后续的相似性度量范围；另一方面，斜率是对序列局部变化方向的描述，但斜率间的数值差异无法准确反映序列局部变化方向的异同，导致最终的相似性度量效果有限。

综上所述，在基于模式序列的趋势相似性度量方面提出了较多的思路和方法，但度量效果并不十分理想，仍然存在较大的改进和提升空间。因此，本文在提出依据分段子序列的均值及其线性拟合函数的导数符号实现模式转换的基础上，以模式之间的异同性比较定义模式匹配距离，借鉴DTW方法的动态规划原理，提出了一种动态模式匹配方法，并分析了该方法的特点。最后，运用实验数据测试了该方法的趋势相似性度量效果。

2 时间序列及其分段模式

2.1 时间序列

时间序列X是由n项与时间顺序有关的数据记录组成的元素的有序集合：

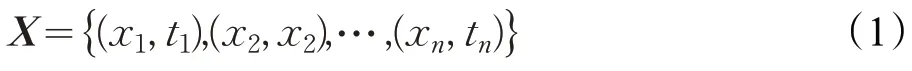
其中，(xi,ti)表示在ti时刻的值为xi，采集时间ti是严格增加的，间隔时间Δt=ti+1-ti通常相同，即ti+1-ti=ti+2-ti+1,因此一般将时间序列X简记为。

2.2 时间序列分段线性表示

时间序列的模式特征是指时间序列的某种变化特征，通过提取时间序列的模式特征，将时间序列变换到模式空间，就得到了时间序列的模式表示[14]。时间序列可以用模式表示如下：

其中，f(w)是时间序列模式表示，e(t)是原序列与它的模式表示之间的误差。将时间序列按时间分成多个子段，如k段，f(w)定义为连接子段两端点的直线段，则时间序列的分段线性表示[14]为：

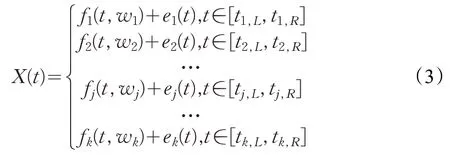
其中，fk(t,wk)表示连接时间序列分段点的线性函数，ek(t)是这段时间内时间序列与它的分段线性表示之间的误差，tk,L和tk,R表示第k段直线的起始时刻与终止时刻，且t1,L=t1,tk-1,R=tk,L,tk,R=tn。

k的值取决于压缩率[15]E，二者之间的关系如式（4）所示。

2.3 模式类型划分

现有研究和方法在将时间序列转化为模式序列时，均单纯以模式作为分段子序列变化趋势的离散化符号，这样虽然可以有效表征局部形态，但可能导致以模式符号有序连接构成的模式序列，难以准确反映时间序列的整体趋势。以最简单的上升、保持、下降三元模式[7]为例，设第j段分段子序列的直线拟合函数的斜率为pj，若pj>0，则该分段的模式为上升，用+表示；若pj<0，则该分段的模式为下降，用-表示；若pj=0，则该分段的模式为保持，用0表示。如图1所示。

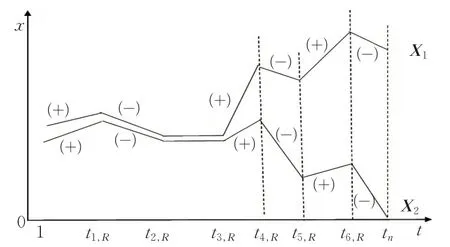
图1 整体趋势不同的时间序列

图1 中，时间序列数据X1和X2被划分为7 个子序列，tj,R表示第j个分段子序列的结束时间，且j=1,2,…,7,tn=t7,R。

如图1所示，图中每个分段括号内为其对应的模式符号，其中+表示上升模式，-表示下降模式，0表示水平模式。从图1中可以看出，X1和X2的模式序列完全一致，但实际上其整体趋势是相反的。因此，时间序列模式转化过程中，不仅要考虑分段子序列的变化方向，而且需包含其均值水平信息，才能使模式符号在反映局部形态的同时，其有序连接组合具备描述整体趋势的能力。

基于上述分析，依据分段子序列的均值及其拟合直线的斜率符号，将时间序列的模式划分为9种，如表1所示。

表1 模式符号对应表

表1中，xˉj表示第j段的均值，pj表示第j个分段拟合直线的斜率，xmin和xmax分别表示时间序列X的最小值和最大值，即xmin=min(x1,x2,…,xn) ，xmax=max(x1,x2,…,xn)，

依据上述定义，时间序列X在划分为k段后，转化为模式化数据，其中zj∈(A,B,C,D,E,F,G,H,I)。

3 动态模式匹配方法

3.1 模式匹配距离

时间序列的模式匹配距离是指，时间序列数据在分段模式化转化后，两种模式之间的距离，即：

从式（5）可以看出，模式匹配距离实际上是分段子序列的模式符号之间的异同性比较，符号相同则距离为0，符号不同则距离为1。

3.2 动态时间弯曲

动态时间弯曲（DTW）是一种通过弯曲时间轴来更好地对时间序列形态进行匹配映射的相似性度量方法。它最早被应用于处理语音数据，后来Berndt等人将它用于度量时间序列的相似性。从此，DTW 在时间序列数据挖掘领域中得到广泛的应用[16]。

DTW 不仅可以度量长度相等的时间序列，也可以对不等长的时间序列进行相似性度量，且对时间序列的突变点或异常点不敏感，比较适用于此类数据的度量，可以实现异步相似性比较[16]。

假设有两个时间序列Q和U，且Q={q1,q2,…,qn}和U={u1,u2,…,um}，那么两个时间序列数据点之间形成的距离矩阵Dn×m={d(i,j)}n×m，其中 1 ≤i≤n，1 ≤j≤m。d(i,j)的值由qi和uj之间的欧氏距离的平方来确定，即d(i,j)=(qi-uj)2。也就是说，矩阵D存储了两个时间序列不同时间点上数据之间的距离[17]。

如图2 所示[17]，图中的每个方格相当于D中元素值，那么DTW 就是从该矩阵中找到一条连续的路径H={h1,h2,…,hs}，使得路径上的元素值相加之和最小，同时这条路径必须满足以下三个条件，即边界限制、连续性和单调性[17]。

图2 动态时间弯曲路径

在矩阵D中，满足以上三个条件的路径有很多，但只需要一条路径作为动态时间弯曲距离，即：

最优路径的查找方法是通过动态规划来实现的，构造一个累计矩阵R={r(i,j)}n×m来记录从起始位置到结束位置的最短路径，且

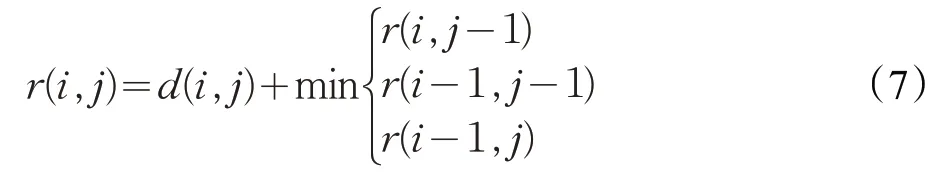
其中，r(0,0)=0，r(i,0)=r(0,j)=∞。

最终两个时间序列的动态时间弯曲距离可由累计距离表示，即LDTW(Q,U)=r(n,m)。由上述算法可以知道，实现长度分别为n和m的两个时间序列之间的动态时间弯曲距离的时间复杂度为O(nm)[17]。

DTW 不要求数据点一一匹配，支持时间轴的伸缩和弯曲，可以有效度量不等长序列的相似性[18]，尤其对时间序列在时间轴上的形状扭曲有非常优秀的辨识能力[5]。但DTW 需要计算基于欧氏距离的代价矩阵及其最优弯曲路径，因此对数值变化敏感，计算复杂度较高，限制了其在大规模高维度时间序列数据中的应用。

时间序列的趋势相似性度量建立在分段模式化基础上，衡量时间序列趋势变化的相似性，尤其是整体趋势的相似性，因此要求相似性度量方法对短期局部的噪声具备较好的抗干扰能力。DTW方法通过弯曲时间轴实现序列的异步相似性度量，使其不仅能够根据时间序列的形态度量相似性，而且异步相似性度量可以有效避免短期局部的噪声对序列趋势相似性的干扰。因此，DTW通过弯曲时间轴的异步匹配原理有利于衡量时间序列的趋势相似性。此外，以模式序列为对象，构建基于模式匹配距离的代价矩阵，在降低时间复杂度的同时，可以有效弥补DTW对数值变化敏感的缺陷，有利于度量大规模高维度时间序列的趋势相似性。

3.3 动态模式匹配

动态模式匹配方法的主要思想，就是遵循动态时间弯曲距离的计算过程，并以两条模式序列的模式之间的匹配距离构建距离矩阵D，最终的累计距离即为两条模式序列的动态模式匹配（Dynamic Pattern Matching，DPM）距离。

假设两个时间序列数据，经过分段模式化后形成两条趋势序列Y4和Y5,Y4={z41,z42,…,z4j,…,z4k},Y5={z51,z52,…,z5i,…,z5v}，Y4和Y5并不一定等长。两条序列Y4和Y5的基元形态之间形成距离矩阵Dk×v={d(j,i)}k×v，其中 1 ≤j≤k,1 ≤i≤v,d(j,i)的值为z4j和z5i之间的模式匹配距离，即d(j,i)=d(z4j,z5i)，以模式匹配距离代替动态时间弯曲距离中计算时间序列数据点之间的欧氏距离，形成模式匹配距离矩阵Dk×v={d(j,i)}k×v={d(z4j,z5i)}k×v。

按照动态时间弯曲距离的求解过程，最优路径的查找方法通过动态规划来实现，以累计矩阵RDPM={rDPM(j,i)}k×v记录从起始位置到结束位置的最短路径。

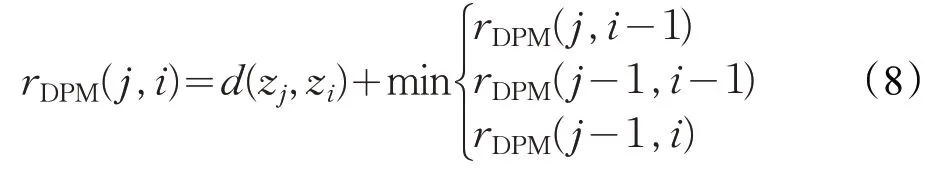
其中，rDPM(0,0)=0,rDPM(j,0)=rDPM(0,i)=∞。

最终，两条趋势序列之间的动态模式匹配距离LDPM(Y4,Y5) 可由累计距离表示，即LDPM(Y4,Y5)=rDPM(k,v)。

3.4 算法分析

DPM方法以模式序列间的动态模式匹配距离来衡量原始时序数据间的趋势相似性，因此，模式序列完整保留原始数据的局部形态与整体趋势信息，是该方法能够准确度量时间序列数据趋势相似性的前提和基础。

作为对模式形态间的异同性比较，模式匹配距离不遵循传统的“模式差异大，则数字距离大”的原则，而是将模式符号看作定性数据，对不同形态之间的差异等同化对待，而没有等级之分与大小之别，且计算过程较为简单，计算量小。

时间序列的分段模式化过程，依据分段子序列的均值及其线性拟合函数的导数符号将时间序列转化为模式序列，不仅降低了序列维度，而且可以在滤除噪声平滑序列的同时，保留序列趋势特征，从而为趋势相似性度量奠定基础。此外，DPM 方法基于模式匹配距离的代价矩阵，寻找最优路径的过程，通过弯曲序列轴允许异步异同性比较，可以避免短期局部的突变过程和异常情况对趋势相似性衡量的干扰。

该方法借鉴了DTW 方法的计算原理，因此继承了其优良特性，不仅适用于序列等长的情况，而且也适用于序列不等长的情况。此外，该方法主要用以度量时间序列的趋势相似性，尤其是整体趋势的相似性，通过异步相似性度量模式序列的趋势相似性，因此不要求序列之间对齐。该方法需要根据序列的变化幅度划分区间，因此主要适用于离线类时间序列数据的相似性度量。而且，划分的区间数量可以根据数据的变化幅度与复杂程度来选择，如当数据值的变化幅度较大，或者各分段线性拟合函数的斜率差异较大时，可以设定较多的模式类型。

根据计算过程，容易分析得到该方法的计算时间效率。长度为n和m的时间序列进行平均分段的时间复杂度分别为O(n)和O(m)，对长度为k和v的模式序列进行DPM距离度量需要的时间复杂度为O(kv)，因此整个算法过程的时间复杂度近似为O(m+n+kv)。因为分段数目k和v通常小于原始序列的长度，所以DPM的时间复杂度O(m+n+kv)要小于DTW的时间复杂度O(mn)，且压缩率越大，二者的差距越大，即DPM 的计算时间效率越高。

4 实验分析

为了验证动态模式匹配方法的可行性及有效性，选取数据集进行实验对比分析。

实验运行环境为 Intel®Xeon®CPUE5-2650 v4@2.20 GHz（2 处理器）、64 GB 内存、512 GB & 7200 rpm SSD 和Microsoft Windows 7 操作系统，开发工具为Matlab2014a。

4.1 实验数据简介

使用UCI 知识发现数据库档案（http：//archive.ics.uci.edu/ml/datasets.html）中的控制图数据，选择其中Normal类的前5个样本数据，Increasing trend类的前5个样本数据，Decreasing trend类的前5个样本数据，共15个时间序列样本数据。每个样本数据等长，均为60 维。各类数据如图3所示。

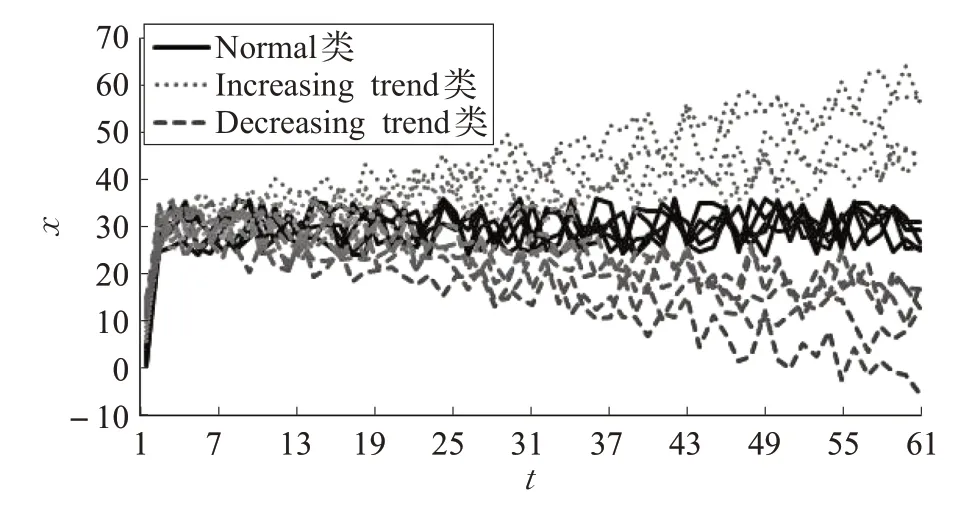
图3 各类时间序列数据

以选择的15 个时间序列样本数据作为实验数据集，其中 Normal 类数据的样本序号依次为 1、2、3、4、5，Increasing 类数据的样本序号依次为 6、7、8、9、10，Decreasing类数据的样本序号依次为11、12、13、14、15。

4.2 实验方案

实验中对时间序列数据进行等长分段直线拟合，即tj,R-tj,L=tj+1,R-tj+1,L=c,c的值与压缩率有关，c=为了避免无法等长分段的情况，最后一段包含剩余时间序列数据点，即tk,R-tk,L=n-c×(k-1)-1，其余分段子序列的长度皆为c。

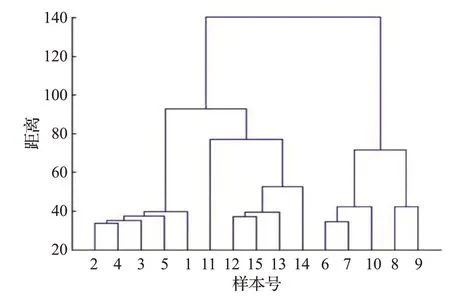
图4 方案1的聚类系统树图

图5 方案2的聚类系统树图

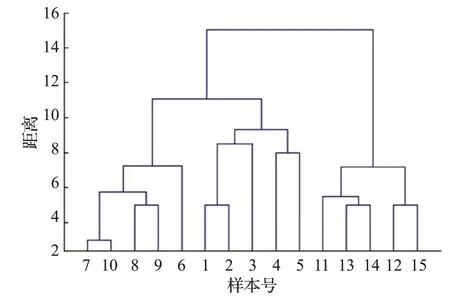
图6 方案3压缩率为50%时的聚类系统树图

对选择的数据使用层次聚类方法进行归类分析，对比欧氏距离、动态时间弯曲距离、动态模式匹配距离之间的相似性度量效果，层次聚类方式均选择average法。

方案1 使用原始数据，以欧氏距离作为原始数据样本之间距离的计算方法。

方案2 使用DTW作为原始数据样本之间距离的计算方法，对原始数据进行聚类。

方案3 在压缩率分别为50%、80%的情况下，针对分段模式转化后的趋势序列，使用DPM 计算趋势序列之间的距离，分析两种压缩率条件下的聚类效果。

方案4 分析DPM对不等长模式序列的趋势相似性度量效果，其中样本4、5、9、10、14、15的压缩率为75%，其余样本的压缩率为80%，且不进行对齐处理。

4.3 实验结果

实验结果如图4～图8 所示，其中图4 为方案1 的聚类谱系图，图5为方案2的聚类谱系图。

由图6、图7可知，动态模式匹配距离的应用效果较好，在压缩数据的条件下依然能准确衡量数据间的趋势相似性。

将上述结果及聚类过程的时间消耗予以统计汇总，结果如表2所示。

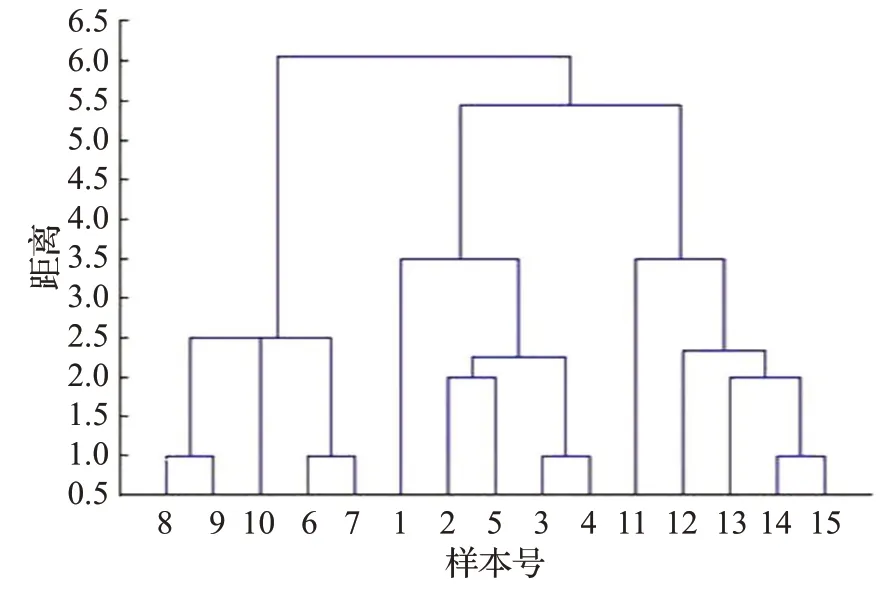
图7 方案3压缩率为80%时的聚类系统树图

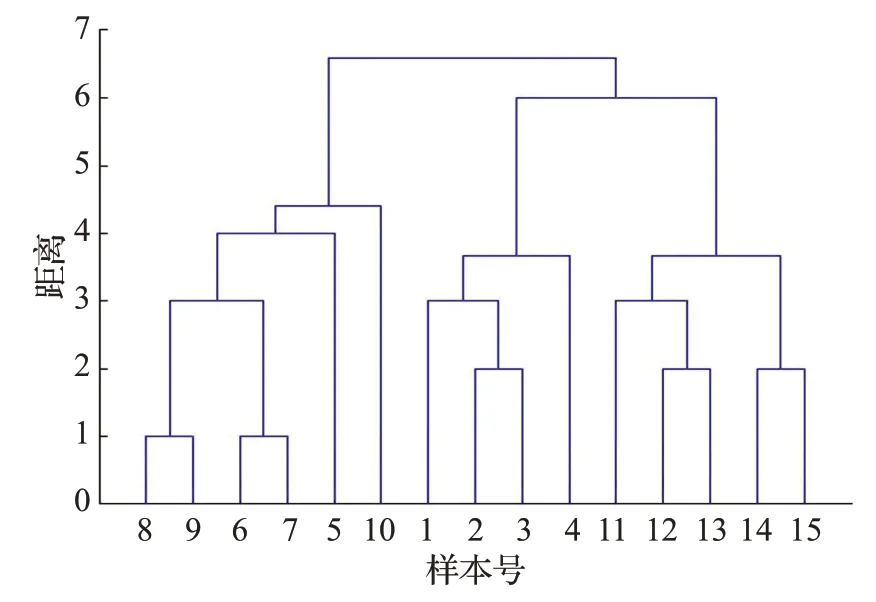
图8 方案4不等长模式序列的聚类系统树图

表2 实验结果

由表2 可知，动态模式匹配距离在压缩率分别为50%、80%的条件下，聚类准确率均为100%，且其时间消耗随着压缩率的增大而极大缩短，远远小于动态时间弯曲的时间消耗，即在保证相似性度量准确率的前提下有效缩短了时间消耗。

方案4 为DPM 方法用于不等长模式序列的趋势相似性度量。由图8 可知，在模式序列不等长的情况下，只有样本5 被错误地划分为Increasing 类，其余样本均实现正确的类别划分，聚类准确率为93%，而且由表2可知，其时间消耗较低，远小于DTW 方法的时间消耗。因此，DPM 方法对不等长序列具有较好的度量效果和性能。

5 结束语

本文在实现时间序列分段线性表示的基础上，依据分段子序列的均值及线性拟合函数的导数符号，实现模式化转化，并以模式间的异同性比较定义模式匹配距离，借鉴DTW方法的原理，构建了一种动态模式匹配方法，用以度量时间序列的趋势相似性。实验数据分析表明，该方法不仅能够在不同的压缩率下准确度量序列间的趋势相似性，且相对于DTW方法，其时间消耗大幅降低。

因此，在分段模式化过程中，不仅要考虑局部趋势方向，而且应该将分段均值水平作为模式划分的标准之一，有利于模式在准确描述局部形态的同时，其有序连接组合能够完整保留时间序列的整体趋势信息，从而为趋势相似性度量奠定良好的基础。另一方面，作为对分段子序列的符号化表示，应该将模式作为定性数据，不同的模式代表不同的局部形态，模式之间并没有等级高低之分，不同模式之间的差异没有大小之别。以时间序列的模式化为基础，挖掘序列频繁模式与关联规则，具有重要价值。

由于动态模式匹配方法可以度量不等长序列之间的趋势相似性，而序列不等长实际上是存在数据缺失情况的一种表现形式，数据存在不同程度的缺失也是不同领域的时序数据挖掘研究所面临的客观现实情况，因此，对于不等长序列的趋势相似性度量效果，尤其是该方法的相似性度量效果与数据缺失比例之间的关系，值得进一步的深入研究。