洞口对带纵向加强肋复合墙体竖向受力性能影响

2020-05-20陈国新阿热帕提艾斯凯尔

科学技术与工程 2020年9期

陈国新，阿热帕提·艾斯凯尔，席亮

(新疆农业大学水利与土木工程学院，乌鲁木齐 830052)

带纵向加强肋复合墙结构是一种在砌体结构中设置多道贯通的截面和配筋较小的钢筋混凝土肋梁作为纵向加强肋的结构形式，钢筋混凝土肋梁与边框柱浇筑成为一个整体，并与保温性能好的砌块逐层砌筑，形成一种各承力部件协同工作的复合型墙体。该结构是由密肋复合板结构派生出的适用于村镇地区低层建筑的抗震、节能于一体的建筑结构体系[1-2]。

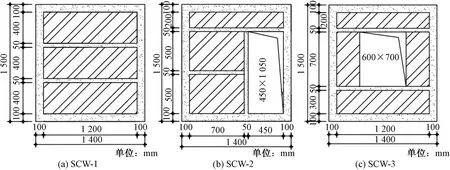
图1 墙体尺寸详情Fig.1 Detail of wall size

近年来，中外专家学者已经对加筋砌块以及配筋砌块剪力墙结构进行了广泛的研究，讨论了影响加筋砌块和配筋砌块剪力墙刚度、承载力等力学性能的因素，并为该结构的后续研究指明了方向。Colangelo[3]对13榀1/2比例的墙体模型进行伪静力试验，结果表明在其他因素相同的条件下，配纵筋较多的墙体抗侧刚度更大，墙体整体性更好；在竖向荷载作用下，有填充砌块的墙体整体变形更小。Haluk等[4]对18榀分别填充有配筋砌块和空心砖砌块的剪力墙进行了抗剪试验，结果表明墙体的纵向配筋率和所承受的竖向压应力大小对墙体的剪切性能影响最大，而墙体的竖向配筋率则对其抗剪能力影响不大；黄炜等[5]对12块密肋复合墙体进行水平荷载作用下伪静力试验，结果表明对于密肋复合墙体三阶段破坏过程来说，剪切破坏属于有利的破坏形式，能够体现出墙体拥有多道抗震防线；黄炜[6]对密肋复合墙体进行水平和竖向荷载作用下的试验，研究结果表明密肋复合墙体边框与框格、框格与內填砌块之间不仅存在良好的协同工作关系，还能将多种力学性能相差悬殊的材料组合成为一种抗震性能良好的复合墙体结构。李启鑫等[7]对4面设置有构造柱的墙体进行轴心受压静力试验，试验结果表明构造柱在墙体中的作用是与圈梁连接形成框格，约束墙体内部填充砌块，不仅增强了墙体的整体性，也大幅提高了墙体的竖向承载能力。王爱民等[8]对5榀1/2比例生态密肋复合墙体进行竖向荷载作用下受压静力试验，结果表明竖向荷载作用下，墙体各构件所承担的轴力主要是按照各构件的刚度进行分配的，边框柱承担了大部分的竖向荷载，肋柱次之。

前人研究表明密肋复合墙体是一种抗震性能良好的墙体结构，墙体的混凝土框格和填充砌块之间能协同受力并且分阶段破坏，竖向荷载在墙体内部各构件中分配传递，并指出洞口是复合墙体竖向承载能力的主要影响因素，但墙体作为建筑结构承担与传递竖向荷载和水平荷载的重要构件，而在实际工程中由于功能需要墙体常会出现开门、窗洞口的情况。开设洞口会破坏墙体的整体性，进而削弱加强肋复合墙体竖向承载力[9]。然而对于开洞墙体在竖向荷载作用下荷载分配情况的研究较少。因此，对2榀1/2比例开门洞和开窗洞的带纵向加强肋复合墙体进行竖向荷载作用下的静力受压试验，探明开洞墙体在竖向荷载作用下的破坏模式和内力分布情况，并与不开洞墙体进行对比，建立墙体数值模型分析洞口变化对竖向承载能力的影响。

1 试验概况

1.1 试件设计

三榀墙体原型设计尺寸均为2.8 m(长)×3.0 m(高)×0.2 m(宽)，采用1/2缩尺比例制作，试验墙体尺寸为1.4 m(长)×1.5 m(高)×0.1 m(宽)，编号分别为SCW-1(未开洞)、SCW-2(开门洞)、SCW-3(开窗洞)。外框梁和外框柱纵筋采用HPB300钢筋，表示为4φ6，箍筋采用冷拔丝，表示为φb4@100；肋梁和肋柱配纵筋4φb4，箍筋采用14号铁丝，表示为14#@100，各试件的尺寸如图1所示。

1.2 加载及墙体测点布置

试验采用100 t液压作动器向试件施加竖向单调荷载，试验加载装置如图2所示。

试验时竖向千斤顶通过水平钢梁向试件施加均布荷载，为保证加载钢梁底部与试件紧密且均匀接触，安装加载钢梁时，在钢梁与墙体顶部铺设1∶2水泥砂浆，并确保钢梁和墙体顶部几何对中。

采用力控加载法对试验墙体进行竖向单调加载。三榀墙体的加载过程均包含预加载和试验两个阶段。预加载阶段均从0 kN开始加载至50 kN，每级荷载25 kN，并持时5 min，再逐级卸载到0。试验阶段墙体SCW-1每级施加荷载50 kN，每级荷载持续时间10 min，加载速率控制在10 kN/min，直至墙体破坏；墙体SCW-2与墙体SCW-3每级施加荷载30 kN，每级荷载持续时间10 min，加载速率控制在10 kN/min，直至墙体破坏。

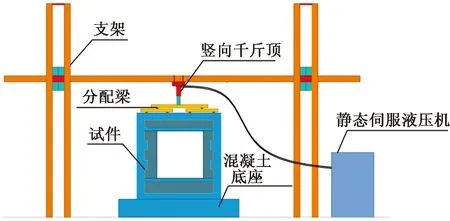
图2 试验加载装置Fig.2 Test loading device

为探明竖向荷载作用下墙体边框柱、肋梁中钢筋的应变状态和整个墙体的变形状态，在三榀墙体边框柱和肋梁钢筋上的相应部位粘贴应变片，并在暗梁顶端左侧、中部和右侧布置位移计，三榀墙体钢筋测点布置如图3所示。

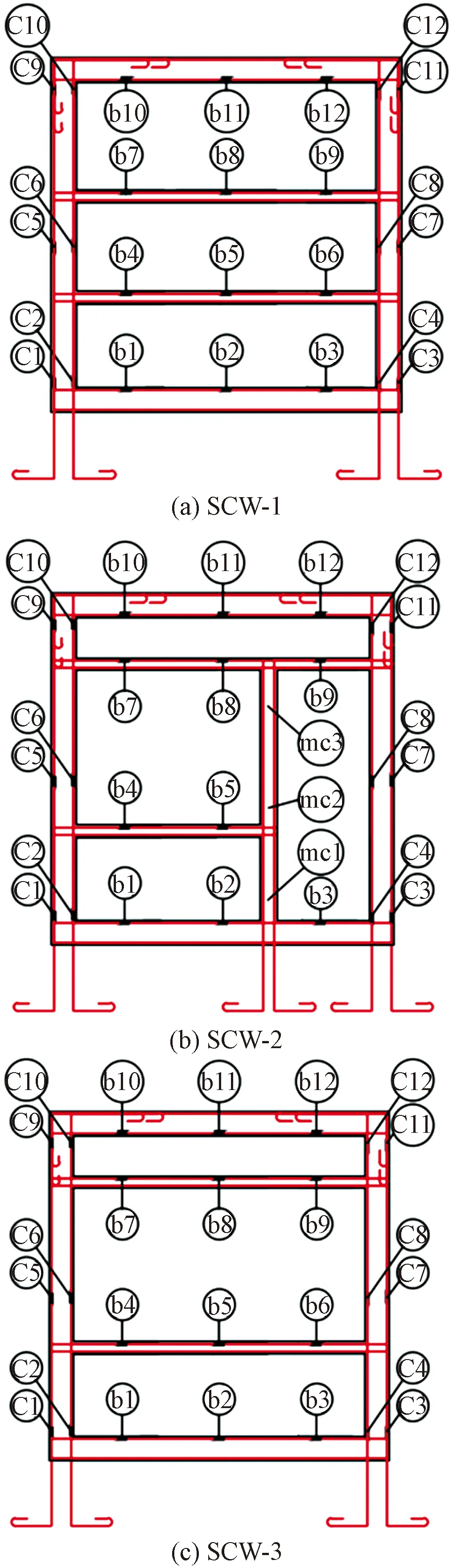
C为柱；b为梁；mc为门洞柱图3 墙体测点布置Fig.3 Measuring point layout of wall

2 试验结果及分析

2.1 墙体破坏过程

3榀墙体竖向受力性能试验结果表明，墙体在加载全过程中主要经历了弹性、弹塑性和破坏三个阶段[10-12]。三榀墙体的破坏过程及最终破坏图如图4～图6所示。

图4 SCW-1破坏过程裂缝图Fig.4 Destruction process crack graph of SCW-1

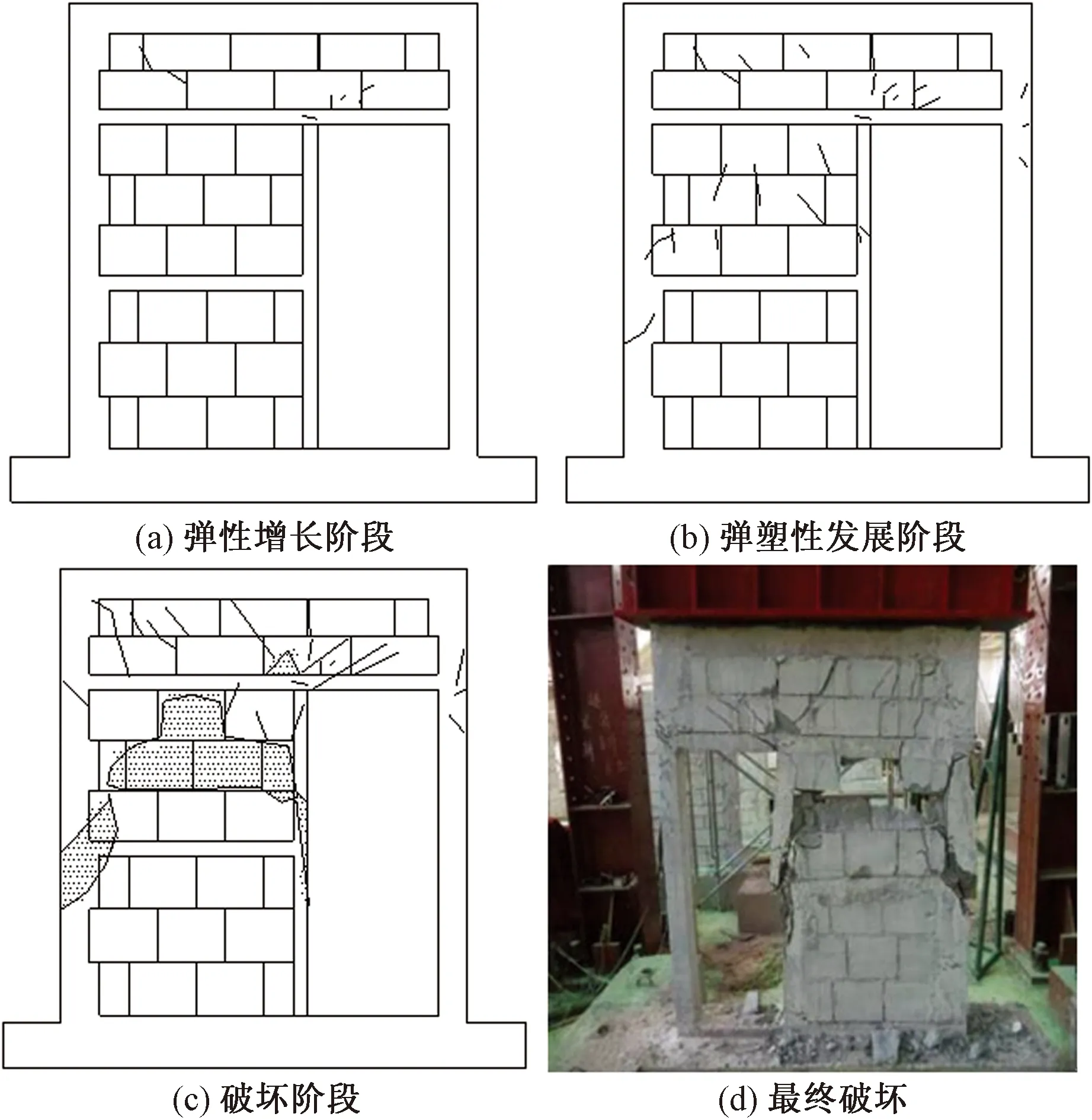
图5 SCW-2破坏过程裂缝图Fig.5 Destruction process crack graph of SCW-2

图6 SCW-3破坏过程裂缝图Fig.6 Destruction process crack graph of SCW-3

2.1.1 弹性阶段

在加载初期，墙体表面未出现明显裂缝，随着荷载逐渐增加，首先在墙体上部砌块表面出现较少细微裂缝，随后伴随着细微的响声，在墙体竖向砂浆缝中出现多道裂缝。随着荷载的不断增加，出现在砌块上的裂缝不断向肋梁与边框柱延伸。此时的竖向荷载约为极限荷载的45%。将此时荷载称为墙体开裂荷载。

2.1.2 弹塑性阶段

当墙体进入弹塑性破坏阶段后，个别砌块角部被压碎，肋梁开始出现贯通裂缝，且不断向暗梁与边框柱延伸。边框柱与暗梁连接角部出现混凝土被压碎并出现明显的裂缝，此时墙体所承受的竖向荷载约为墙体极限荷载的70%～80%。

2.1.3 破坏阶段

墙体进入破坏阶段后，砌块部分脱落，肋梁与边框柱连接处混凝土开裂明显，边框柱侧面竖向裂缝不断变宽并向两端延伸，两侧边框柱与暗梁连接处混凝土被压碎，导致部分钢筋外露。此时，墙体大部分混凝土被压碎，钢筋已经屈服，墙体破坏。

2.2 墙体荷载-位移曲线

在墙体顶部两个边缘和中部位置设置三个位移计，读取不同荷载级别下墙体顶部的竖向变形，三榀墙体顶部荷载-位移曲线如图7所示。

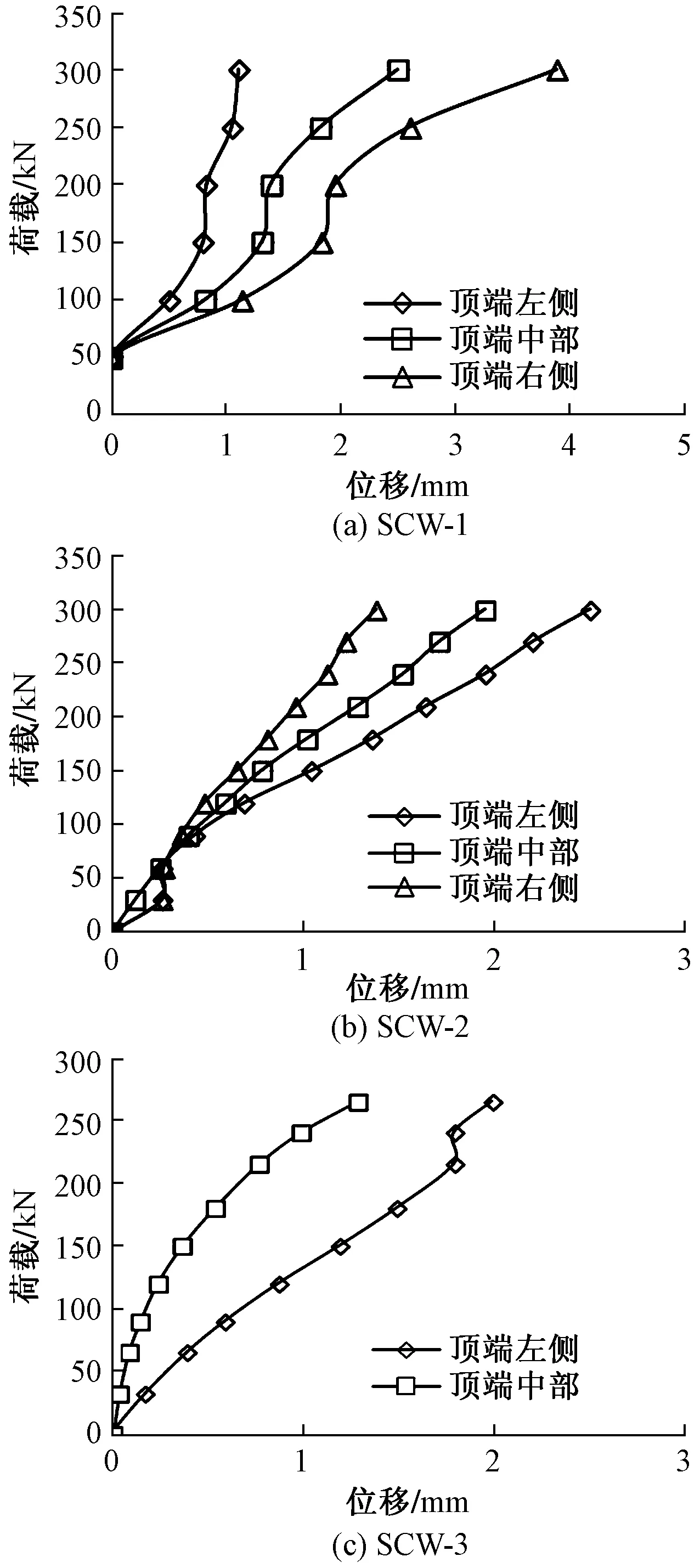
图7 试验墙体顶部荷载-位移曲线Fig.7 Load-displacement curve at the top of the test wall

由图7可以看出，在竖向荷载到达50 kN之前，墙体SCW-1顶部位移非常小，此时墙体整体性也较为完好，未出现明显破坏现象；竖向荷载由50 kN加载到175 kN过程对应于墙体的弹塑性受力阶段，此时荷载-位移曲线也反映为线性增长趋势；荷载继续增加，位移随荷载增加趋势变缓，此时墙体即将进入破坏阶段；当墙体进入破坏阶段后，荷载已经不再随位移的增加而提升，宣告墙体破坏。墙体SCW-2在竖向荷载加载到75 kN之前顶部位移增长缓慢且左右两端荷载-位移曲线大致重合；随着荷载的不断增大，墙体顶部两端的位移都在不断增大，但因为开门洞的原因，墙体右侧刚度比左侧小，导致加载过程中荷载向刚度较大的墙体左侧集中，所以在加载过程中墙体左侧位移一直大于右侧位移。墙体SCW-3在加载初期荷载-位移曲线增长较为平稳；从70 kN加载至210 kN期间，位移增速较快，此时墙体正处于砌块和肋梁受力的弹塑性阶段；在210 kN加载至250 kN过程中，曲线有一段位移没有增长，但荷载迅速提升阶段，此时墙体砌块和肋梁均被破坏，边框柱开始承受竖向荷载，因前期边框柱承重较少也未出现明显的破坏现象，所以此时边框柱对承载力有一个迅速的提升；同墙体SCW-1一样，墙体SCW-3在接近极限荷载时其荷载-位移曲线并未出现明显拐点，但此时荷载已不再继续增长，墙体已破坏。

2.3 钢筋应变

2.3.1 外框柱钢筋

图8为墙体边框柱钢筋应变随荷载变化规律。由图8(a)可以看出，除边框柱上部截面外，墙体SCW-1边框柱各截面钢筋应变-荷载曲线变化趋势基本相同，且大致分为三个阶段。荷载由0 kN增加至150 kN时，各截面钢筋应变增速较快，但荷载提升缓慢，此时墙体正处于弹性阶段，钢筋未出现塑性屈服；当荷载由150 kN增加至200 kN时，曲线突然变陡，钢筋应变几乎不再增大，但荷载迅速增长。此时对应于墙体的弹塑性破坏阶段；当荷载继续增加至250 kN时，荷载随钢筋应变变化趋势明显变缓。此时墙体SCW-1已接近于极限荷载，各部位钢筋基本屈服。

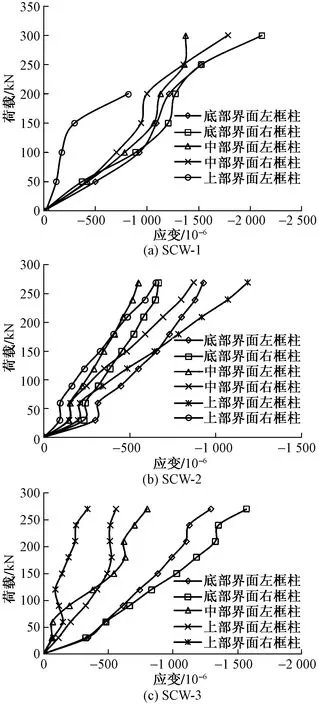
图8 墙体边框柱钢筋应变变化规律Fig.8 Change law of steel strain in wall frame column

由图8(b)可以看出，墙体SCW-2各截面钢筋应变随荷载变化趋势大致相等。在荷载由0 kN增加至第一级荷载30 kN时，各截面钢筋应变增长速度较快；在荷载由30 kN增加至60 kN时，出现了短暂的强化阶段，荷载迅速提升，但钢筋应变增长速率缓慢；荷载从60 kN增加直到墙体破坏这一过程中，各截面的钢筋应变-荷载曲线均基本呈线性增长。在加载全过程中，墙体右边框柱底部钢筋应变均小于左边框柱底部钢筋应变，主要原因是由于墙体两侧竖向刚度不均匀产生的。

由图8(c)可以看出，左右边框柱底部钢筋应变-荷载曲线发展过程相差较大，但都当荷载到达30 kN时出现拐点。在加载初期30～60 kN时有一小段强化阶段，强化阶段过后墙体进入弹塑性破坏阶段；当加载至210 kN时，曲线出现明显拐点，钢筋进入强化阶段，荷载上升迅速，应变增长缓慢，此时墙体即将进入破坏阶段；荷载增加至240 kN以后，钢筋应变又开始出现明显增长，但增长速率比第一阶段缓慢，此时墙体已基本被破坏。

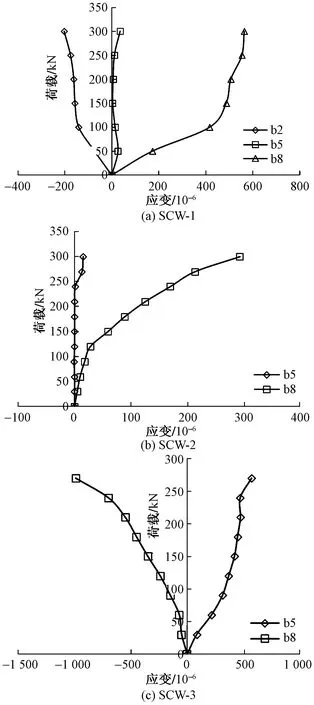
图9 肋梁钢筋应变变化规律Fig.9 Strain variation law of rib beam

2.3.2 肋梁钢筋

带纵向加强肋复合墙体共设置三道肋梁，取每榀墙体各道肋梁中部测点所测得的钢筋应变数据进行分析。墙体肋梁中部钢筋应变-荷载曲线如图9所示。

由图9(a)可知，未开洞墙体SCW-1各道肋梁中部钢筋应变状态相差悬殊，墙体底部钢筋始终处于压应变状态，墙体上部肋梁钢筋则始终处于拉应变状态，但位于墙体中部肋梁的钢筋则表现为很小的拉应变，并有向压应变过渡的趋势。三道肋梁中部钢筋在加载初期应变值都很小，但当加载至100～150 kN时，曲线出现明显拐点，此时砌块已被完全破坏并退出工作，肋梁开始承担更多的竖向荷载。

图9(b)为开门洞墙体肋梁钢筋应变变化规律。由于下层肋梁中部应变片损坏，因此未能获得下层肋梁中部应变信息。由图可以看出，墙体SCW-2中部肋梁钢筋几乎没有出现应变，只是在外荷载超过250 kN时产生了较小的拉应变。墙体上部肋梁钢筋始终处于拉应变状态，且当竖向荷载达到120 kN时，钢筋应变-荷载曲线出现明显拐点，此时墙体进入第二受力阶段，肋梁开始承担主要竖向荷载。

由图9(c)可知，在竖向荷载作用下处于窗洞下部肋梁钢筋始终处于压应变状态，窗洞上部肋梁钢筋则始终处于拉应变。当荷载增加至250 kN左右时，曲线出现明显拐点，肋梁钢筋基本屈服，墙体处于破坏阶段。

3 洞口率和洞口位置对墙体竖向承载力影响

3.1 数值模型验证

根据试验墙体尺寸依次建立墙体各部件，并参考文献[13]对于多种复合材料相接处时主从面的连接方式进行拼装，选取理想的本构模型来定义混凝土、钢筋和加气块等材料的本构关系[14]。将墙板中的箍筋和纵筋通过merge命令组成钢筋笼，并选用Embedded Region命令嵌入混凝土中，使用Creat Boundary Condition命令对复合墙板模型的底部进行完全固结，通过Creat Load命令对暗梁上表面完成竖向加载的设置，全程采用力控制。试验墙体模型及钢筋骨架模型如图10、图11所示。

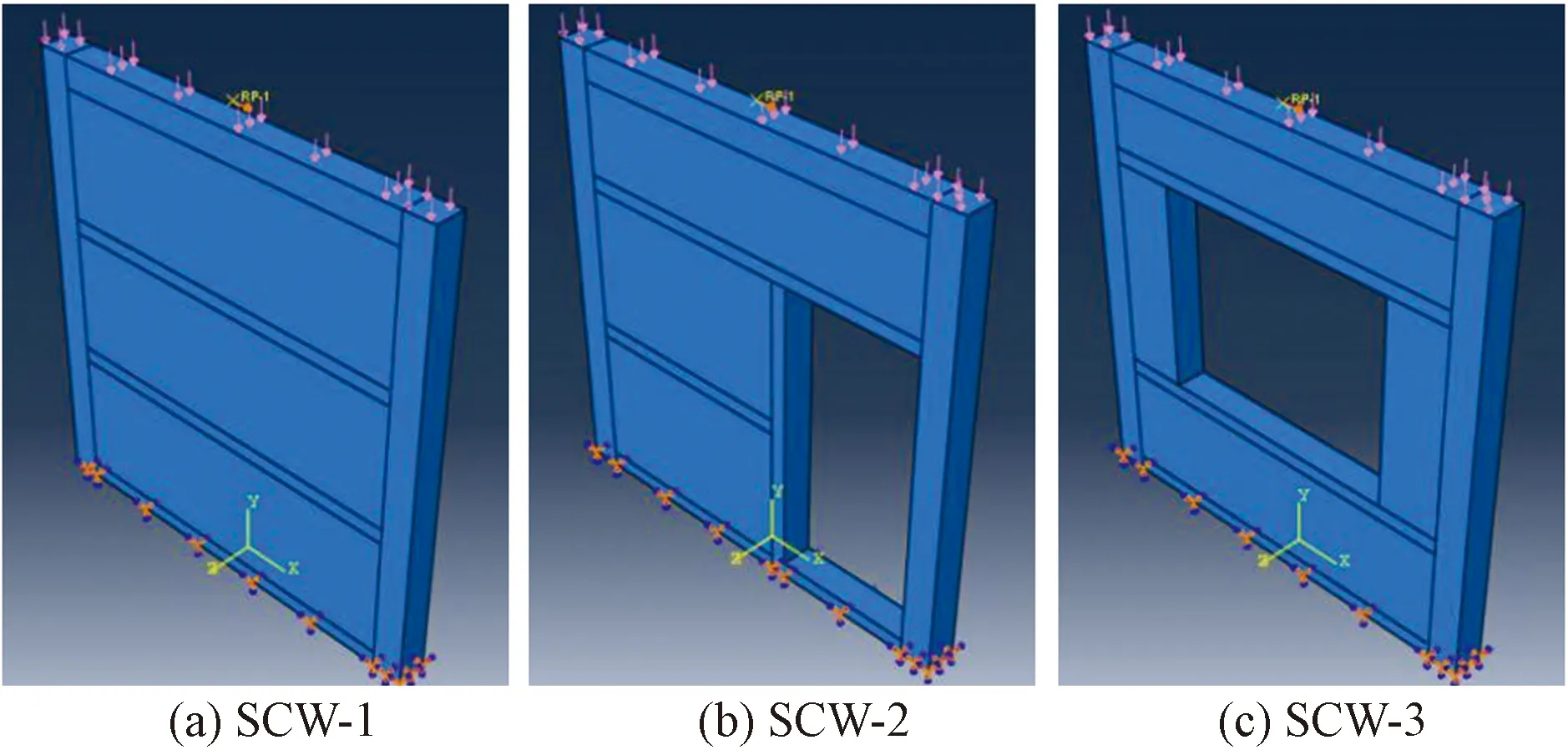
图10 复合墙体整体模型Fig.10 Overall model of composite wall

图11 试验墙体钢筋骨架模型Fig.11 Test the steel frame model of the wall

3榀试验墙体试验和有限元分析对比结果如表1所示。由表1可知，墙体承载力有限元模拟结果和试验结果有一定的偏差[15-17]，有限元模拟结果略大于试验结果，分析其原因，主要有以下几个方面：①数值模拟时将加载条件理想化，而与实际情况下的加载有一定的偏差；②墙体数值计算中未考虑内填砌块之间的拼缝及材料初始缺陷的影响；③内填砌块与混凝土肋格、外框之间未考虑接触属性的影响，与实际情况存在一定的偏差，但相对偏差为4.6%～7.2%，偏差较小。建立的带纵向加强肋复合墙体数值模型具有一定的适用性和精确性，建模过程可为其他不同工况下的墙体模型提供参考依据。

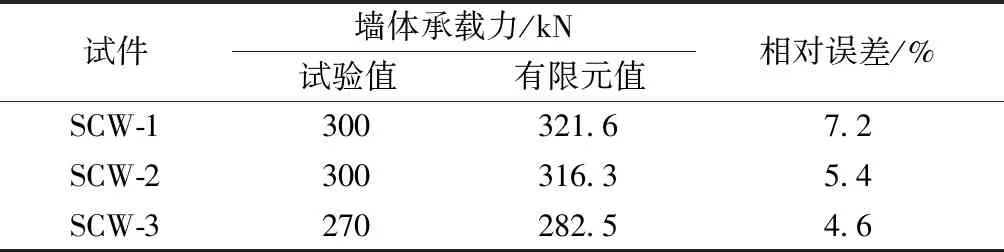
表1 墙体承载力试验和有限元结果对比Table 1 Bearing capacity test of wall and comparison of finite element results

3.2 不同开洞工况对承载力影响研究

不改变墙体的外框尺寸，考虑洞口位置和洞口率变化的影响，建立不同开洞工况墙体数值模型进行计算，并与未开洞墙体的极限荷载进行对比，结果如表2所示。

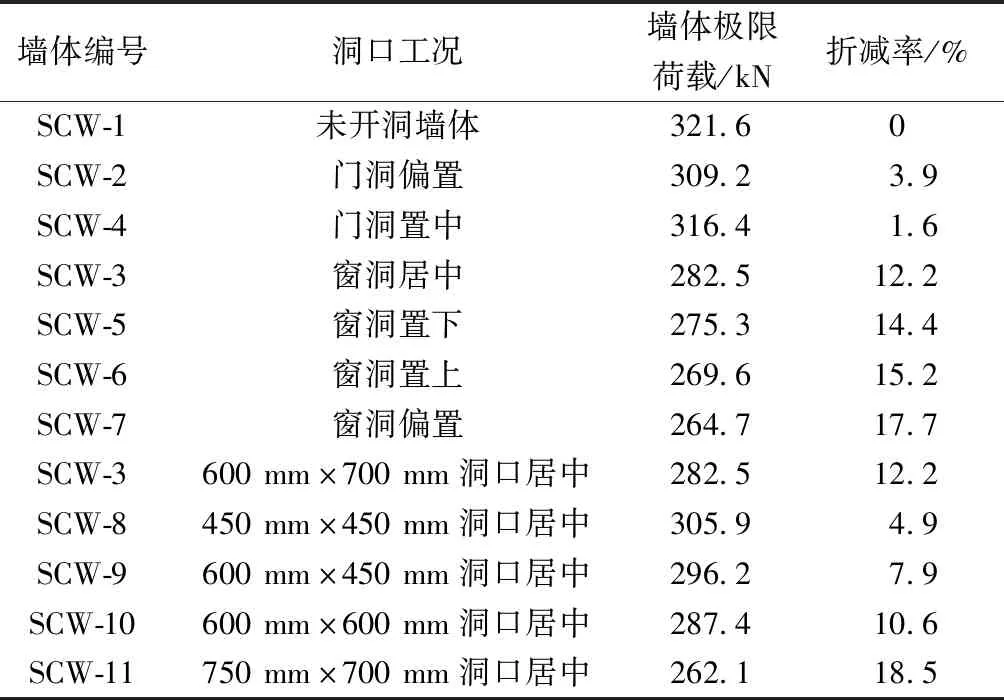
表2 不同工况墙体模型有限元分析结果Table 2 Finite element analysis results of wall model under different working conditions

注：门洞置中是指门洞居中布置于墙体，门洞偏置是指门洞一边为外框柱；窗洞置下是指窗洞底距离底边肋梁250 mm，窗洞置上是指窗洞底距离底边肋梁600 mm，窗洞偏置是指窗洞边距离外框柱250 mm。

由表2可知，不论是门洞还是窗洞，相同洞口率情况下改变洞口位置，对墙体竖向承载力的影响并不明显。在洞口位置固定的情况下，改变洞口率的大小对墙体承载力的影响程度较大[18-20]，尤其是在洞口大小超过600 mm×600 mm，洞口率的改变对墙体竖向承载力的影响更加明显。因此，仅取影响墙体竖向承载力的主要因素洞口率的大小来考虑其对墙体竖向承载力的折减程度。

3.3 洞口折减系数

利用有限元分析结果，取洞口布置居中的墙体模型，运用IBM SPSS Statistics软件对洞口率和折减率进行一元线性回归分析，分析结果如表3～表5所示。

表3 回归模型摘要Table 3 Summary of regression models

注：R2为拟合优度

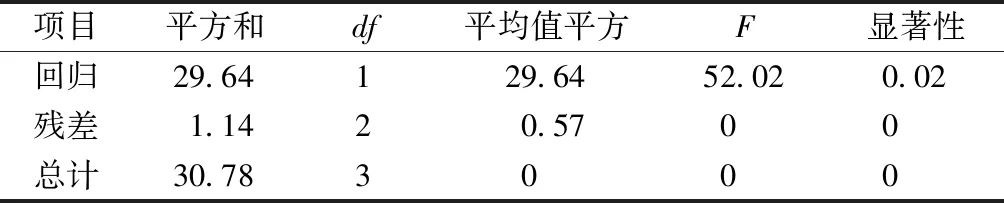
表4 变异数分析Table 4 Analysis of variance

注：df为自由度；F为回归均方与残差平方的比值。

表5 回归系数Table 5 Regression coefficients

注：B为非标准化回归系数；β为标准化回归系数，T为回归系数检验值。

通过表3～表5墙体模型折减率与洞口率一元线性回归分析结果可以得知，回归模型调整后R2为0.94，接近于1，说明回归模型拟合度较高，回归方程显著性检验的概率为0.02，小于显著水平0.05，则认为当系数不同时为0.02时被解释变量与解释变量全体的线性关系是显著的，可以建立线性方程。由系数表可知，洞口率与承载力折减率之间的一元线性方程表达式为

y=0.614x-0.480

(1)

由开洞率和折减率的一元线性回归分析可知，洞口率与折减率之间存在0.614倍的线性关系，因此，建立洞口折减系数λ表达式为