基于相关旁瓣平均的混沌码与线性调频复合调制无线电引信抗数字射频存储干扰方法

乔彩霞, 郝新红, 陈齐乐, 孔志杰, 王雄武

(1北京理工大学 机电动态控制重点实验室， 北京 100081； 2.中国运载火箭技术研究院， 北京 100076)

0 引言

伪码调相与线性调频复合调制引信既具备调频信号良好的距离分辨力和多普勒容限性，又保留了伪码的相关性，在引信抗干扰方面具有独特的优势[1-2]。但随着电子对抗技术的发展，数字射频存储(DRFM)干扰机的研制、装备使得无线电引信的生存受到严重威胁。与传统瞄准式[3-4]和扫频式[5-6]干扰相比，DRFM干扰的典型特征是能够截获、存储引信发射信号，并经延时、放大后转发出去[7]。DRFM干扰信号与引信发射信号高度相干，对以相关算法定距的复合调制引信造成严重威胁。

针对DRFM干扰，国内外提出了大量抗干扰方法，其中发射波形去周期化设计是一个重要的发展方向。DRFM利用引信发射信号的周期重复特性干扰引信，其干扰信号总是滞后于真实回波信号至少一个调制周期[8]。因此通过采用发射信号频率捷变[9]、变调制率[10]、脉冲分集[11]及随机相位调制[12]等技术，能够去除引信发射信号的周期重复特性，提高引信的抗DRFM干扰性能。发射波形去周期化设计抗DRFM干扰的关键在于各个调制周期的发射信号波形正交，使得DRFM干扰信号经过引信相关处理后完全被抑制。但严格意义上的正交往往较难实现，因此通常采用准正交的发射波形，并设计相应的相关旁瓣抑制方法来降低非严格正交造成的影响[13]。混沌码作为一种新兴的伪码，具有初值敏感性、非周期性、随机性和类正交等特性，广泛应用于雷达探测、保密通信等领域[14]，其在抗DRFM干扰方面具有独特优势。

本文为提高伪码调相与线性调频复合调制无线电引信的抗DRFM转发式干扰性能，设计了混沌码与线性调频复合调制引信发射波形，该发射波形采用混沌码控制线性调频信号相位反转。针对DRFM干扰总是滞后于真实回波信号至少一个调制周期的特性，混沌码与线性调频复合调制波形不同调频周期采用不同初值的混沌码调相，实现发射波形去周期化；在信号处理模块，提出相关旁瓣平均(ARS)算法获得引信相关输出的统计特征，抑制混沌码非严格正交对引信造成的影响。理论分析和仿真结果表明：基于ARS的混沌码与线性调频复合调制引信抗干扰方法能够显著抑制引信相关旁瓣，提高无线电引信的抗DRFM干扰性能。

1 DRFM干扰作用下伪码调相与线性调频复合调制引信的响应

1.1 伪码调相与线性调频复合调制引信原理

伪码调相与线性调频复合调制引信原理如图1所示，调制信号模块产生锯齿波调制信号，控制射频压控振荡器(VCO)产生锯齿波调频信号，伪码模块产生伪码序列控制调相器对锯齿波调频信号二项调制产生复合调制信号，经环形器由收发共用天线辐射出去；目标回波信号同本地参考信号混频获得携带目标信息的复合调制差频信号，经视频放大、模数转换后送到信号处理模块，经瞬时相关谐波解调(ICHD)定距算法提取目标信息。图1中,st(t)为发射信号，sr(t)为目标回波信号，sref(t)为本地参考信号，sid(t)为差频信号，scor(t)为瞬时相关后所得信号，m0为所选定谐波次数，τ0为引信预设起爆延时，B为调制频偏，fm为调制频率，fd为多普勒频率。

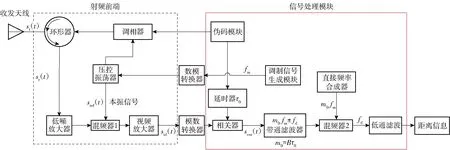
图1 复合调制引信原理框图Fig.1 Block diagram of hybrid modulation fuze

设引信发射信号时间t，则伪码调相与线性调频复合调制发射信号sPN(t)可表示为

(1)

令tn=t-nPTc，则发射信号可以简化为

(2)

假设引信同目标初始距离为R，弹目径向相对运动速度为v，则目标回波信号sr(t)可表示为

sr(tn,τ)=Ar(τ)sPN(tn-τ)，

(3)

(4)

通常情况下，引信探测距离较近，回波信号时延τ≪PTc,可以忽略复合调制差频信号非规则区，其可简化为

(5)

引信采用ICHD定距算法，若引信预设起爆延时τ0，则信号处理电路首先将模数转换后的复合调制差频信号与延迟τ0的伪码作瞬时相关，以保存伪码的相关特性：

(6)

scor(tn,τ)的第m0=βτ0次谐波系数X(m0,τ)满足：

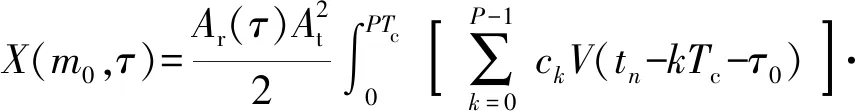
(7)

(8)

分析(8)式可知，复合调制差频信号与延时混沌码瞬时相关所得信号m0次谐波包络受发射信号自相关函数调制，当τ=τ0时，m0次谐波包络为相关主瓣，在其他位置为相关旁瓣。将m0次谐波经2次混频、低通滤波后，最终获得多普勒信号，该多普勒信号继承了谐波幅度包络，通过对多普勒信号进行包络检波、门限比较，可以获得目标距离信息。

1.2 DRFM复合调制引信的影响

DRFM干扰机通过截获、存储引信发射信号，并延时、转发实施干扰，利用引信发射信号的周期调制特性干扰引信，干扰信号总是滞后于真实回波信号1个周期。为提高干扰效率，干扰机通常采用多时延叠加的干扰方式，若假设干扰机采用L个时延，则干扰信号可表示为

(9)

式中：Al表示干扰机的功放增益；τl为干扰信号的延时。引信发射信号为周期调制信号，满足周期重复特性st(tn-1-τl)=e-j2πφ0st(tn-τl)，因此干扰信号可转化为

(10)

式中：φ0为干扰信号滞后于本地参考信号所引入的初始相位，φ0=2πf0+πβPTc. 在干扰作用下，复合调制引信输出的差频信号(以下简称干扰差频信号)可表示为

(11)

干扰差频经ICHD算法处理输出后，有

(12)

DRFM成功干扰引信存在两种情况：1)干扰信号与引信发射信号高度相干，干扰作用下引信输出包络受发射信号自相关函数调制，对于任意τl，在满足τl=τ0时，引信在DRFM干扰作用下输出相关峰主瓣，使得引信被干扰；2)干扰机功放增益较大，干扰信号功率远远大于引信真实回波信号功率，即使所有τl都无法满足τl=τ0时，较大的相关旁瓣仍有可能使得引信被干扰。

2 基于ARS的混沌码与线性调频复合调制引信抗DRFM干扰方法

基于ARS的混沌码与线性调频复合调制引信抗DRFM干扰方法原理如图2所示。与伪码调相与线性调频引信相比，引信发射波形采用混沌码控制调频信号的相位反转，且不同调频周期采用不同初值混沌码调相，实现发射波形去周期化；信号处理系统采用ARS算法，该算法利用快速傅里叶变换(FFT)代替带通滤波实现谐波解调，并将G次频谱FFT所得结果累加平均，获得引信相关输出的统计特征，利用混沌码相关旁瓣的统计特性进一步抑制DRFM干扰。

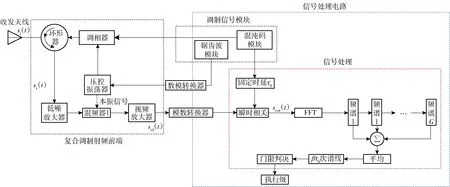
图2 基于ARS的抗干扰方法原理图Fig.2 Schematic diagram of anti-jamming method based on averaging of correlation side lobes

2.1 混沌码与线性调频复合调制发射波形

引信发射信号产生方式如图3 所示，控制相位反转的混沌码由logistic映射产生的混沌序列经2值量化所得。针对线性调频信号的不同调制周期，采用不同初值的混沌码调相，实现发射信号波形去周期化设计。

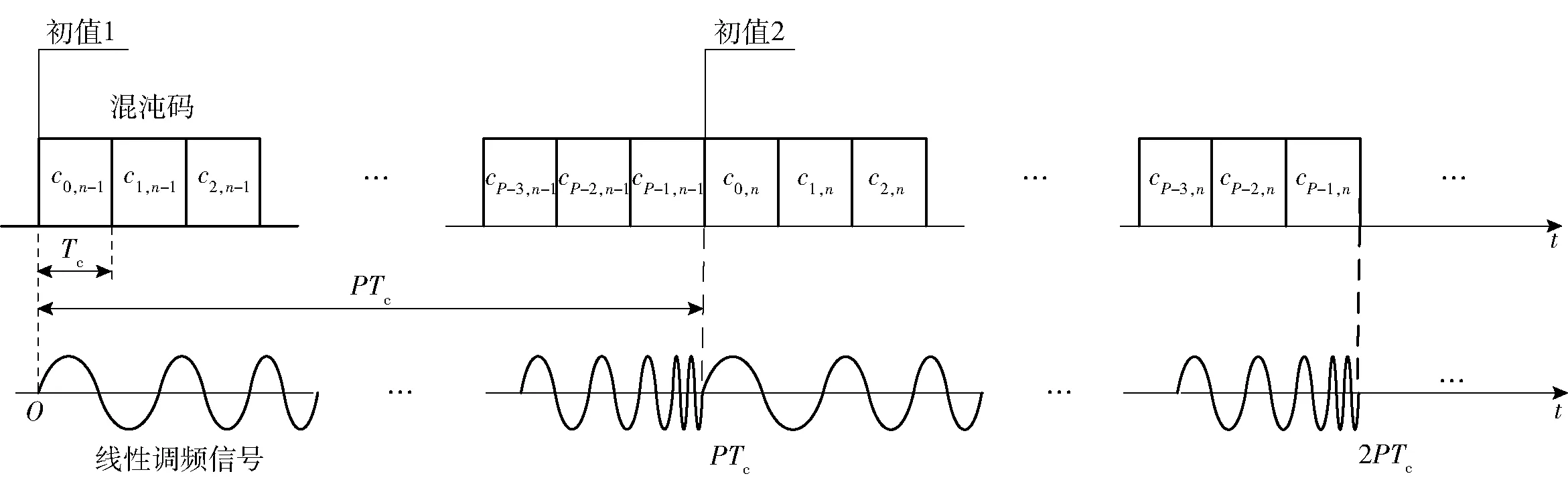
图3 混沌码与线性调频复合调制发射信号Fig.3 Binary phase-coded chirp waveforms

混沌码与线性调频复合调制发射信号可以表示为

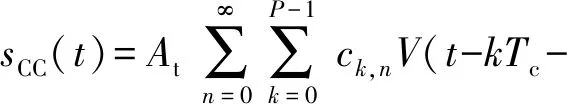
(13)

引信任意两调频周期发射信号波形互相关函数为

(14)

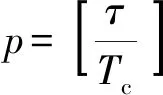
(15)

即混沌码与线性调频复合调制发射信号保留了混沌码的类正交特性，其互相关函数低于混沌码的互相关值。

2.2 ICHD算法的FFT实现

由于弹目相对运动速度v≪c，一个调频周期时长内弹目距离可以认为稳定不变，此时回波信号时延可以建为离散模型

(16)

式中：δ=vPTc. 复合调制差频信号可被重新定义为

(17)

(17)式本质上是对(4)式中时延变量τ的离散采样，经瞬时相关后可得

(18)

对scor(tn,nδ)连续地作时长PTc的FFT运算，FFT输出结果可以表示为

(19)

第m=m0次谐波包络为

|S(m0,n)|=Ar(τn)Ra(τn-τ0),

(20)

对scor(tn,nδ)连续地作FFT运算可直接获得复合调制差频m0次谐波包络，其包络为发射信号自相关函数的离散采样，采样间隔为PTc.

2.3 ARS算法定距原理

假设G个调频周期时长内，弹目相对距离变化对复合调制差频信号频谱X(m,n)的影响可以忽略，将引信G次频谱FFT所得相关输出作累加平均，即可得到引信相关输出的统计特征：

(21)

(22)

当G取值足够大时，G次FFT所得ARS后其幅值为0，SG(m0,n)满足：

(23)

2.4 DRFM干扰抑制原理

假设干扰信号时延τl<2PTc，在DRFM干扰作用下，混沌码与线性调频复合调制引信干扰差频信号可表示为

(24)

干扰差频信号经相关处理后，所得m0次谐波包络如下：

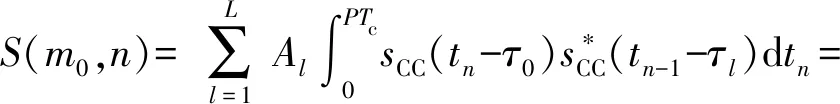
(25)

ARS算法输出结果为

(26)

(27)

DRFM干扰作用下，引信m0次谐波包络受发射信号波形互相关函数调制，由于混沌码与线性调频复合调制信号保留了混沌码的类正交特性，引信不会出现相关峰，但干扰信号功放增益远远大于目标有效散射面积，存在AlRc(τl-τ0)>Ar(τ)·Ra(0)的可能性；而采用ARS算法，则可以显著抑制相关旁瓣，进一步提高引信抗干扰性能。

3 仿真与分析

本节采用MATLAB软件进行仿真验证，分析基于统计特征的混沌码与线性调频复合调制无线电引信的抗干扰性能。仿真参数设置如表1所示，其中DRFM干扰采用5个延时叠加的干扰策略，干扰距离100 m.

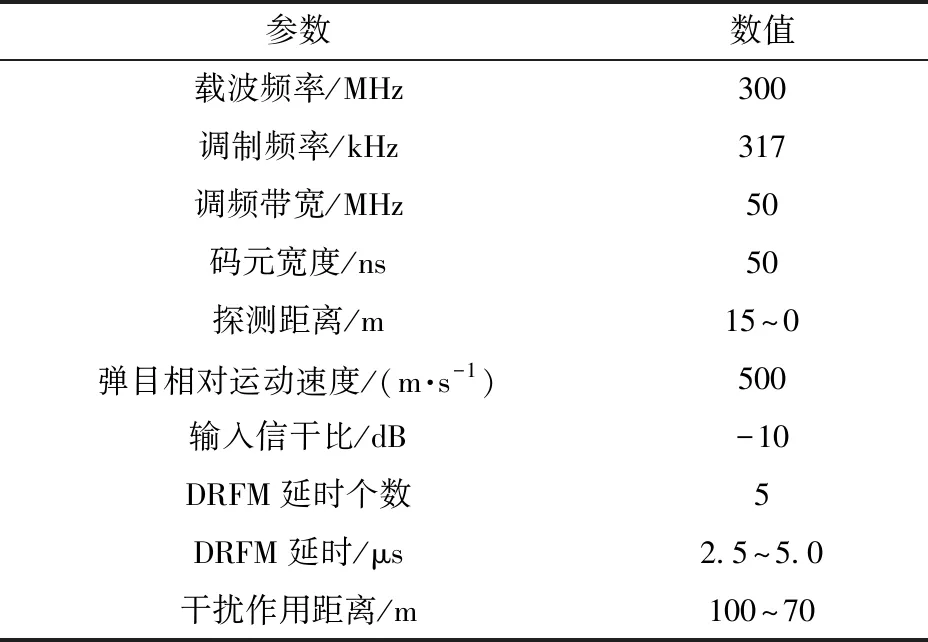
表1 仿真参数Tab.1 Simulation parameters

3.1 定距及相关旁瓣抑制性能

ARS算法是在ICHD定距算法基础上，将引信相关输出平均处理，以达到旁瓣抑制的目的。算法定距性能仿真结果如图4(a)所示。在G分别取值为10、50和100，以及引信在R=6 m时，输出宽度为(6±3) m的主瓣，距离分辨力与ICHD保持一致。将引信输出转化为图4(b)所示形式，ICHD算法输出相关旁瓣约为-22.3 dBm,G=10时ARS算法输出-31.5 dBm,G=50时ARS算法输出-39.7 dBm,G=100时ARS算法输出-43.9 dBm. ARS算法有效地抑制了复合调制引信的相关旁瓣，且随着G取值的增大，算法抑制性能不断提高。但算法输出主瓣随着G取值增大略有下降，这是因为随着G值的增大，累加的各个周期差频信号频谱逐渐不再可以近似认为稳定不变。

图4 定距算法仿真结果Fig.4 Simulated results of the ranging method

3.2 复合调制引信抗干扰性能

在DRFM干扰作用下，复合调制无线电引信的相应如图5所示，其中DRFM采用多延时叠加的干扰策略，干扰信号包括5个延时的截获信号，总信干比为-10 dB. 伪码调相与线性调频复合调制无线电引信在DRFM干扰作用下输出结果如图5(a)所示，由于未采用任何抗干扰措施， 引信分别在96 m位置、91 m位置、86 m位置、80 m位置和75 m位置分别输出5个峰值，且引信输出峰值与真实回波信号作用下输出结果基本相同，即引信完全被干扰。

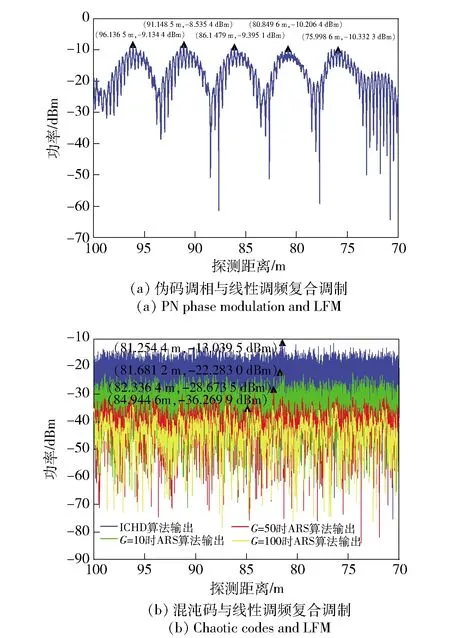
图5 复合调制引信在DRFM干扰作用下的输出Fig.5 Output of hybrid modulation fuze under DRFM jamming

伪码调相与线性调频复合调制无线电引信在DRFM干扰作用下输出结果如图5(b)所示，由于采用了发射波形去周期化的抗干扰方法，采用ICHD算法定距的复合调制引信在DRFM干扰作用下输出结果为相关旁瓣，其相关旁瓣结果约为-13 dBm. 与ICHD算法对比，当G=10时ARS算法输出约为-22 dBm;当G=50时ARS算法输出约为-28 dBm;当G=100时ARS算法输出约为-32 dBm. 表明与ICHD算法对比, 算法ARS能够显著提高混沌码与线性调频复合调制无线电的干扰抑制性能，将干扰作用下引信输出抑制效果提高大约20 dB.

4 算法实测验证

在信干比为-10 dB时，干扰信号和目标回波信号同时存在的条件下,引信输出结果如图6所示，其中图6(a)为ICHD算法输出，图6(b)、图6(c)和图6(d)分别为G=10、G=50和G=100时ARS算法的输出。由图6可见，由于信干比较低，采用ICHD算法时，目标信号完全淹没在干扰信号下，引信基本丧失定距功能；而ARS算法则能够有效抑制DRFM干扰，且随着G值增大，抑制效果逐渐提高。

图6 干扰作用下引信的响应Fig.6 Output of the fuze under DRFM jamming

5 结论

为提高复合调制无线电引信的抗DRFM干扰性能，设计了去周期化的复合调制无线电引信发射波形，并提出了ARS的抗干扰方法，进一步抑制DRFM干扰对复合调制引信的影响。由于DRFM干扰信号总是滞后于真实回波信号至少一个调制周期，引信发射信号不同调频周期采用不同初值的混沌码调相后，在干扰作用下复合调制引信输出相关旁瓣；采用相关旁瓣累计平均的抗干扰方法可以充分利用混沌码相关旁瓣的统计特性，通过合理选择G的取值，能够有效提高干扰抑制效果大约20 dB.