超大吨位非对称曲梁转体斜拉桥称配重技术

陈美军

(中铁六局北京铁建公司，北京 100036)

实践中为保证转体施工的安全平稳进行，需进行称重试验确定桥梁偏心，并加以配重保证转体桥梁球铰中心承重。研究表明，在梁体重量大、纵横向不对称、不平衡力矩大的情况下进行转体，势必造成梁体称重顶力大、转体桥梁上转盘空间有限的问题，可能出现无足够空间布置称重千斤顶的情况，造成超大吨位不对称梁体称重无法完成；同时，不对称梁体在大偏心距的情况下冒然解除砂箱约束，让单组撑脚承受大偏心距造成的支撑反力，可能超过撑脚设计的极限承载能力，存在较大的安全隐患。本文采取先理论配重再解除转盘约束，然后进行称重，最后根据称重的结果调整配重的方式，解决了超大吨位非对称曲梁转体斜拉桥称重难题，同时确保了施工安全。

1 工程概况

唐山二环路上跨津山铁路等既有铁路立交桥全长927.5 m，由转体斜拉桥、转体T构桥、引桥组成，斜拉桥与T构桥共用墩柱，分别设置支座，两联梁体处设置伸缩缝。受下穿铁路和上跨铁路的影响，桥梁纵坡设计为3.84%。斜拉桥为独塔四索面低梁体预应力混凝土桥，半漂浮体系，跨径(34+81)m+115 m，主塔高80.5 m，主梁曲线内外侧宽度分别为19 m，转体梁长为2×106.5 m，位于半径为6 000 m的曲线上，转体吨位33 000 t，转体采用下转体方式，转体角度42°3′18″。球绞直径5.5 m，转体滑道直径15 m，上转盘长24.2 m，宽16.2 m，高2 m，转体牵引系统(布置见图1)设置2对牵引索。

图1 转体系统结构(单位：cm)

2 称、配重试验方案

2.1 施工难点

(1)受斜拉桥副跨辅助墩上方中横梁混凝土影响，纵向不平衡力矩为177 532 kN·m，通过试算，纵向偏心达到54.9 cm，克服不平衡力矩和摩阻力矩称重所需顶力高达45 000 kN，解除约束后撑脚受力超限，存在极大安全隐患。

(2)上转盘空间位置有限，没有足够空间布置所需顶力的千斤顶。

(3)因转体梁三面均为既有线路，同时斜拉索索间距小，常规配重材料无法通过吊车吊到桥面上进行配重。

2.2 理论配重计算

为了解决超大吨位、大偏心距造成称重顶力大的难题，采取先理论配重的方式消除不平衡力矩。根据梁体浇筑的混凝土方量，计算出理论偏心距，计算原理如图2所示。

图2 偏心距计算原理

(2)

(3)

式中：G2为副跨一侧梁体重力；G1为主跨一侧梁体重力；L1、L2分别为主副跨梁体距转动球铰几何中心的距离；G为转体重量；e1为配重后转动体理论偏心距(取5 cm)；L为配重位置距离球铰中心距离。

由上式计算可得，不平衡力矩MG=177 532 kN·m，偏心距e=54.9 cm(偏小里程一侧)。

据此，为实现桥梁重心在小里程侧5～10 cm 范围内，应在大里程方向配重。根据梁面实际情况，在距离桥梁中心100 m位置具备配重条件。根据计算，如在100 m位置配重，偏心距为5 cm时需配重165 t，偏心距为10 cm时需配重148 t。考虑到本转体桥重量大，配重时按照偏心5 cm进行考虑，即需要配重165 t，经与监控单位核实，在距离塔柱中心100 m位置配重165 t，梁体受力在允许范围内，梁体处于安全状态。

2.3 理论配重实施

根据理论配重分析，在距离塔柱中心100 m位置配重165 t。为了解决梁端紧邻既有线、梁侧面斜拉索密集等导致无法支立吊车吊装配重材料的问题，采取水袋配重的方式进行配重，避免大型吊车作业，同时通过加放水能够达到配重调整的目的。配重示意图如图3所示。

图3 水袋配重位置平面图(单位：m)

根据桥面宽度，订制了8个水袋，每个水袋可盛水25 m3，注水时通过水表确定每个水袋的实际注水方量，以达到精确配重的目的。为了防止转体期间梁体颤动导致水袋不稳，施工现场通过搭设支架对水袋进行固定。现场配重情况见图4。

图4 施工现场水袋布置

3 现场称重试验

3.1 称重试验前准备

转体桥梁临时约束由4组砂箱和8组撑脚组成。在称重之前需将砂箱拆除，同时将撑脚与滑道之间的石英砂清扫干净，桥梁仅靠球铰支撑。砂箱解除时，采取对称的方式拆除，在拆除期间对桥梁整体沉降做好观测，拆除完成后测量每个撑脚和滑道之间的间距，为选择滑块厚度提供依据。

3.2 测点布置

在桥梁转动体两侧的临时支承处布置千斤顶，用以在称重试验时对转动体进行顶放，在每台千斤顶上设置荷重传感器，测试试验过程中支点的支反力值。

在球铰上转盘四周布置多个百分表，用以判断转动体在称重试验过程中是否发生转动以及进行撑脚位移测试，测点布置如图5所示。如果发现所有撑脚均未与滑道钢板接触，说明梁的平衡处于“转动体球铰摩阻力矩大于转动体不平衡力矩”的状态[1]。

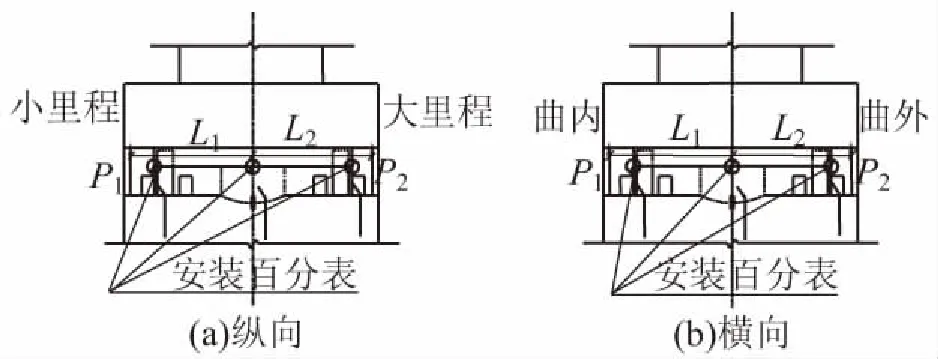
图5 千斤顶布置图

称重过程中，虽然梁底位移变化较小，但是由于桥梁悬臂较长，为了验证梁底位移及试验安全，在梁端通过悬坠铅垂测量梁端竖向位移。

3.3 测试内容和方案[1，2]

3.3.1 摩阻力矩及不平衡力矩测试

施工支架拆除后，转动体的平衡体系将出现下列两种情况中的一种：

(1)转动体球铰摩阻力矩(MZ)大于转动体不平衡力矩(MG)。这种情况梁体不发生绕球铰的刚体转动，体系的平衡由球铰摩阻力矩和转动体不平衡力矩所保持。

3.3.2 摩擦系数及偏心距

4 试验结果分析

4.1 纵桥向

根据现场情况，当桥梁解除约束后，所有撑脚均不接触滑道，可以判断：摩阻力矩Mz大于不平衡力矩MG，需要两侧顶升称重试验。

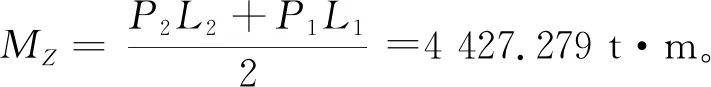
4.2 横桥向

根据现场情况，当桥梁解除约束后，所有撑脚均不接触滑道，可以判断：摩阻力矩Mz大于不平衡力矩MG。因此，横桥向也需要两侧顶升称重试验。

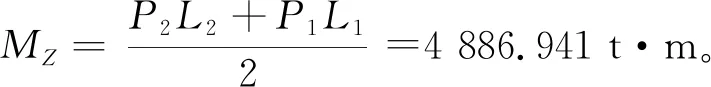
根据称重结果，纵桥向向大里程偏心9.8 cm。通过原因分析，理论配重计算时假定沿桥梁方向混凝土浇筑偏差是一致的，实际因箱梁施工过程中浇筑节段多，每一段混凝土偏差存在一定的差异。为了达到偏心5 cm的目标，通过计算，需要将距离桥中心100 m位置通过放水减配重48.86 t，此时桥梁重心将由大里程侧的9.8 cm处转移到小里程侧的5.0 cm处。横桥方向，曲线内侧偏重，偏心距为10.6 cm。因进行称重试验时，力臂取值为施力点到上转盘几何中心的距离，偏心距数值以上部结构几何中心为参考系，根据设计图纸，球铰中心已从结构几何中心向曲线内侧设预偏心12 cm，因此横桥向实际偏心距为1.4 cm，不再进行配重调整。

5 结束语

本文以33 000 t转体斜拉桥为背景，主要探讨了大吨位纵横向不对称、不平衡力矩大的梁体称重配重问题。现场通过称重试验，在理论配重完成后，实际称重顶力纵桥向最大为1 036 t，横桥向最大为1 287.8 t。在现场条件受限的情况下，采用水袋装水作为配重材料，达到了快速、便捷、经济的目的。称重时采用同步顶升系统进行顶升，根据撑脚与滑道间距设置顶升位移量，实现位移与顶力进行双控，确保了顶升过程中的安全。调整完配重后，在正式转体时，在大里程侧的2组撑脚与滑道接触，与重心向小里程侧偏移5 cm能够吻合。本工程采取的称配重方案和措施，取得良好的效果，可为同类工程参考。