预制圆管顶管允许最大顶力的解析公式及其应用探究

范毅雄

中国市政工程中南设计研究总院有限公司 430010

引言

验算预制管接头传力面所能承受的最大顶力，是顶管设计和施工中的一项重要内容。如果顶管管道处于理想的轴心受压状态，其允许最大顶力的计算将是简单的，但实际施工时管道产生偏转是不可避免的，另外曲线顶管时管道也会产生偏转，因此管道接头传力面实际上几乎总是处于偏心受压状态，此时的允许最大顶力计算相对比较复杂。目前我国工程建设协会顶管规范《给水排水工程顶管技术规范》（CECS246：2008）［1］第8.1.1条的允许最大顶力计算公式是参考的美国土木工程师协会《Standard Practice for Direct Design of Precast Concrete Pipe for Jacking in Trenchless Construction》（ASCE27-00）［2］，其假定条件为：顶力合力偏心，管道接头传力面的压应力呈三角形分布，一侧压应力为零、另一侧压应力最大。在这种特例下，偏压合力刚好是理想轴压合力的一半，因此公式中取折减系数为0.5。但对于其余偏心条件下，例如曲线顶管顶力合力偏心较大使得管道接头接触面发生脱离时的最大允许顶力如何计算，ASCE27-00［2］没有给出具体的计算公式，中国规范［1］则只在条文说明中给出了未求解的积分式。本文将推导圆环截面线性分布压力的合力及弯矩的解析公式，并探讨可用于指导设计和施工的实用计算方法。

1 圆环截面线性分布压力的有关解析公式

为推导圆环截面压应力线性分布时的解析公式，需要先推导圆盘截面的公式，再以外圆减内圆来推导圆环截面的公式。

1.1 圆盘截面的有关公式

如图1所示，其中D1为直径，r为半径，压应力线性分布，pmax为应力最大值，pmin为应力最小值，受压区高度Z＝λD1，λ为受压区间比，是一个无量纲系数。

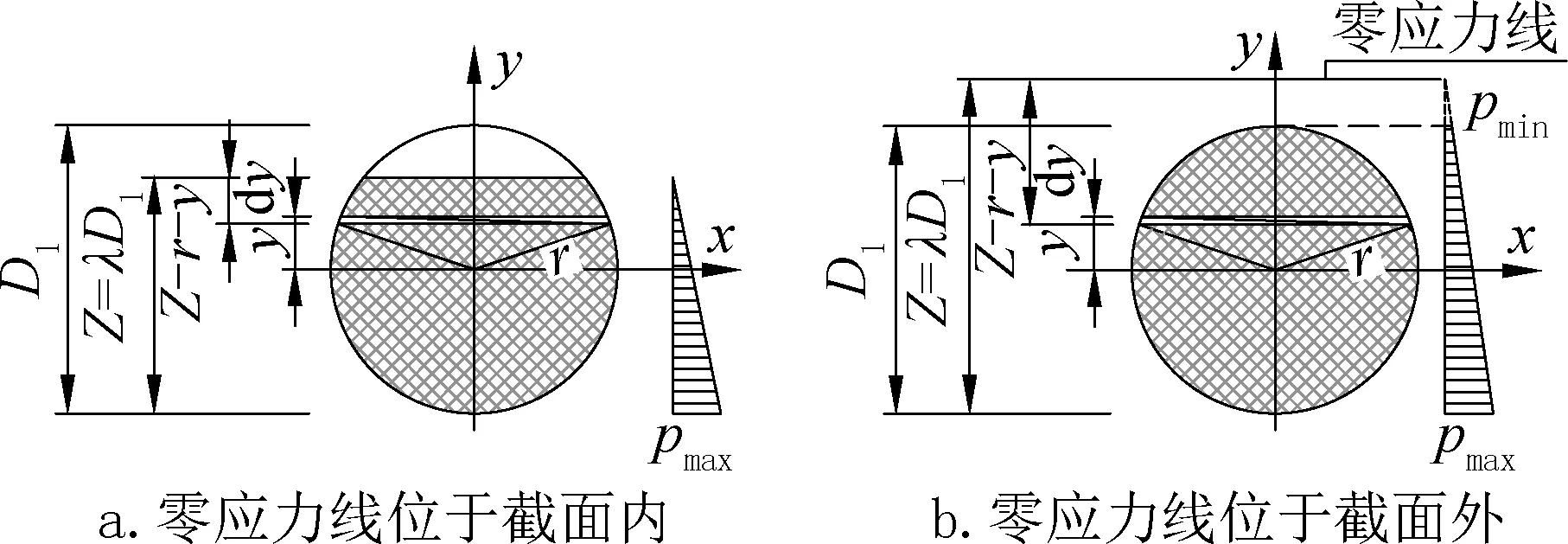
图1 圆盘截面积分计算简图Fig.1 Diagram for calculating the integral of disk section

（1）零应力线位于截面内，即0≤λ≤1时。

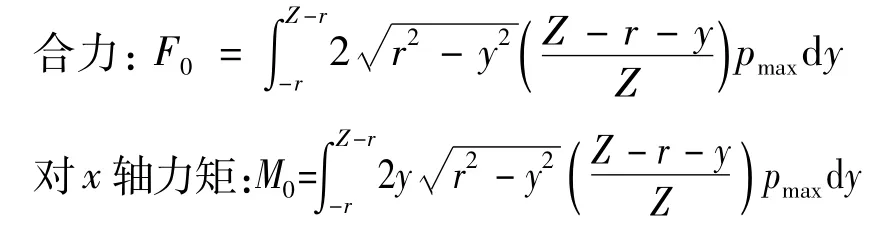
求解并代入r＝D1/2，Z＝λD1，得：

（2）零应力线位于截面外，即1≤λ时。

1.2 圆环截面的有关公式

利用公式（1）～公式（4），就可以推导出以下公式。

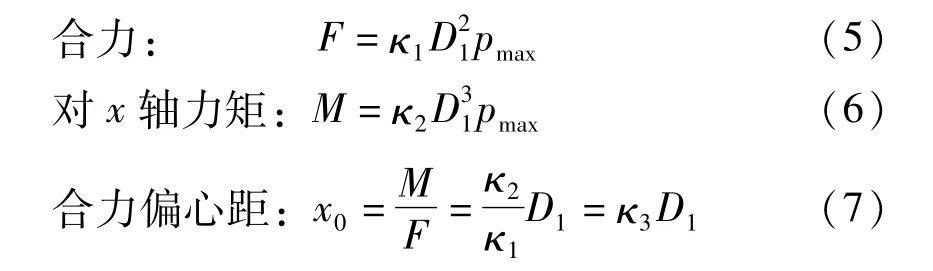
式中：D1为圆环外径；λ为受压区高度和外径的比值，β为圆环内径D0和外径D1的比值，均为无量纲参数。合力系数κ1按表1计算，力矩系数κ2按表2计算，合力偏心距系数κ3由κ1、κ2计算。

表1 合力系数κ1Tab.1 Resultant force coefficient κ1

表2 力矩系数κ2Tab.2 Moment coefficient κ2

表1、表2中的四种条件对应于压应力分布情况，如图2所示。

图2 圆环截面积分计算简图Fig.2 Diagram for calculating the integral of ring section

需要注意的是，由于计算模型所取的坐标系，推导的公式计算所得κ2为负值，相应的κ3和偏心距也是负值，应用时可视需要改为正值。

2 顶管接头变形约束条件

为了确定允许最大顶力和管道偏转角、管线转弯半径之间的关系，还需要考虑管道接头处的变形。

1.顶管接头全截面受压

顶管接头处于全截面受压时，其受力简图如图3所示；其中α为木垫圈的厚度，D1此处为木垫圈外径，L为管节长度，R为管道转弯半径，φ为管道接头偏转角，t为管壁最薄处厚度，hp为木垫圈宽度，Ep为木垫圈材料弹性模量，Ec为管材弹性模量。

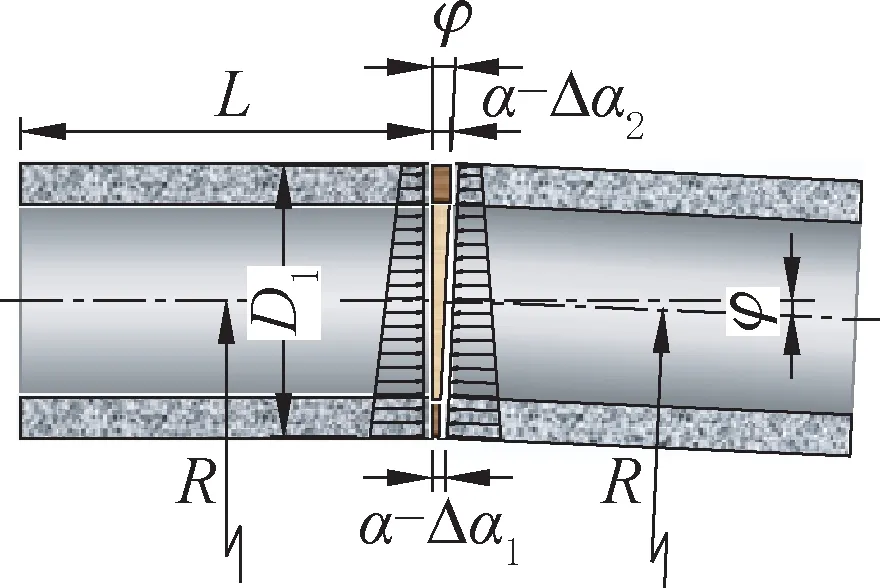
图3 接头全截面受压的计算简图Fig.3 Calculation diagram of full section compression of joint

分别计算两边的压缩变形量（Δα1、Δα2），压缩变形包括木垫圈的变形（Δαp1、Δαp2）和管道的变形（Δαc1、Δαc2），得到公式（8）。

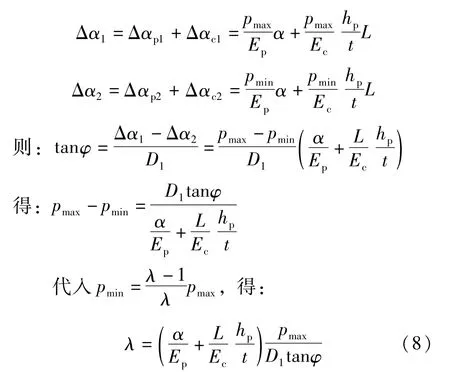
2.顶管接头存在脱离区

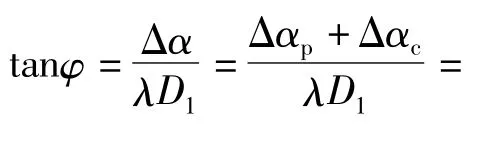
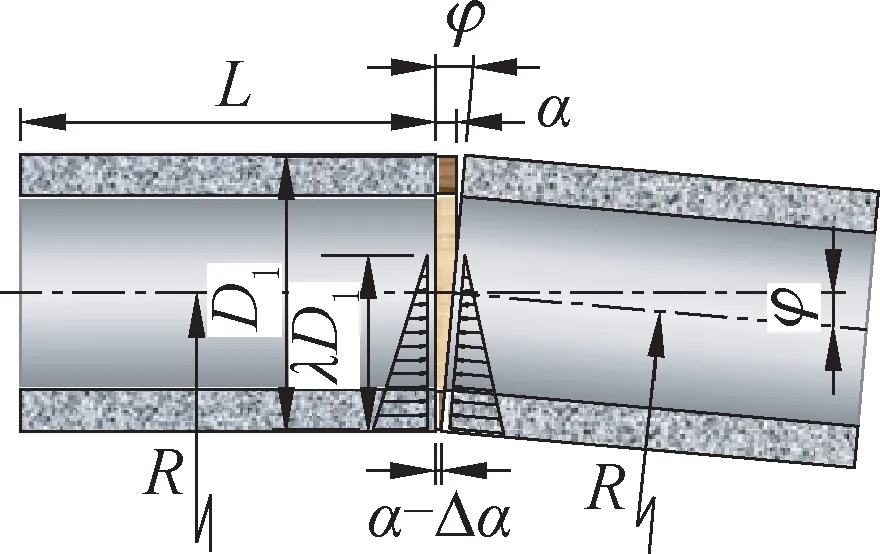
图4 接头张开的计算简图Fig.4 Calculation diagram of joint opening

所以两种情况下受压区间比λ和偏转角φ之间关系式是统一的，按公式（8）计算。

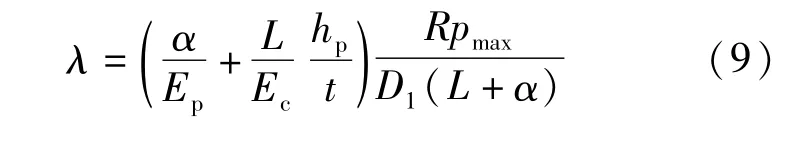
3 公式应用

以上各变量中管道尺寸由D1和β表示；pmax表示管道接头截面的最大应力，在计算允许最大顶力时取管材抗压强度设计值，例如混凝土管取pmax＝fc；管道顶力偏心分别由λ、x0、φ、R这四个变量表示，这四个变量是相互关联的，可利用公式（7）～（9）由其中任一个求得其余三个，λ作为基础变量通过公式（5）和截面压应力合力相关联；另外公式（8）、（9）中的各个变量由管道接头的构造和材料确定。

3.1 允许最大顶力公式

为方便应用，采用理想轴压条件下允许最大顶力的折减形式，参考CECS246［1］第8.1.1条的公式，允许最大顶力标准值为：

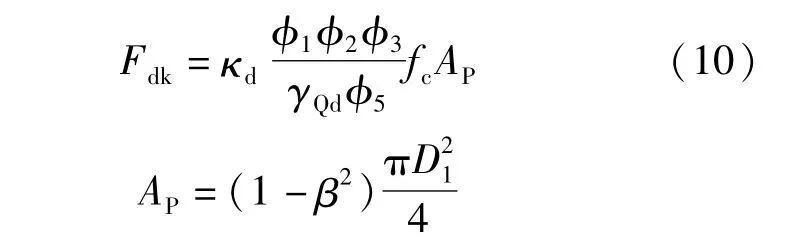
式中：φ1、φ2、φ3、φ5、γQd、fc同CECS246［1］定义，γQd为顶力分项系数，fc为混凝土受压强度设计值，φ1、φ2、φ3、φ5为混凝土管材相关的一系列调整系数，其他管材则取相应的另一系列调整系数；AP为管道最小有效传力面面积；κd为偏心折减系数，由公式（5）可得：

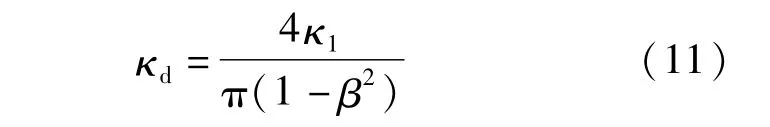
以下讨论如何具体应用公式（10）、（11）。

3.2 设计取值

1.直线顶管

公式（10）、（11）是通用的，适用于任意偏心状态的顶管，因此如果设计时对直线顶管施工偏心（包括管道接头偏转角、顶力合力偏心距）作出合理限制，也可以根据这个限制值计算相应的允许最大顶力，而不是固定地取折减系数0.5。

2.曲线顶管

对于曲线顶管，设计时可根据公式（9）由管线转弯半径R求得λ，再利用公式（10）、（11）计算允许最大顶力。

当1＜λ时：κd＝1-1/2λ，计算较简单。

当0＜λ＜1时，κd的解析公式较复杂，为方便应用，本文根据解析公式绘制了图表供查询。由于κd是λ和β的二元函数，可以绘制二维函数的等高线图如图5所示。例如取λ＝0.75、β＝0.8，图中交点处κd＝0.389，和解析公式计算结果0.388765一致。

图5 折减系数κd随λ和β变化的等高线Fig.5 The contour map of Reduction coefficient κd with λ and β

3.3 施工控制

施工控制主要是控制顶力的大小和偏心，或者是已知偏心状态求允许最大顶力，或者是已知顶力大小求允许最大偏心。如前所述，表示顶力偏心的四个变量为λ、x0、φ、R，以下分别讨论。

1.管道接头接触面受压区间比

当管道接头接触面出现脱离区域时，可以从管道内部直接测得受压区间比λ，就可以利用公式（10）、（11）或图5计算此时的偏心折减系数κd，进而得到允许最大顶力。

2.顶力合力偏心距

顶管施工时，工作井内的主压千斤顶、工具管后的校正千斤顶以及中继间处的中继千斤顶的顶力大小是已知的，可以由此计算得到顶力合力的偏心距x0，从而计算得到合力偏心距系数κ3，再利用公式（7）计算得到λ，最后由λ计算κd。但公式（7）较复杂，实际应用时可以直接查询图6得到。

图6 折减系数κd与合力偏心距系数κ3的关系Fig.6 Relationship of the reduction coefficient κd and the relative eccentricity coefficient κ3

当偏心距小于断面核半径，接头接触面全截面受压时，可推导得：κd＝1/［1＋8κ3/（1＋β2）］。

例如β＝0.8、κ3＝0.1时，查图6得κd＝0.67，由上面的公式计算得κd＝0.672。

当施工顶力已知，需要计算允许最大偏心距时，可采用公式（10）由顶力计算得κd，然后查图6得κ3，从而算出该顶力作用下的允许最大偏心距。

3.偏转角和转弯半径

已知偏转角和转弯半径求允许最大顶力，采用第3.2节曲线顶管设计中的方法。

当施工顶力已知，求允许最大偏转角或允许最小转弯半径时，可采用公式（10）由顶力计算得κd，然后查图5或利用公式（11）求得λ，再利用公式（8）求得允许最大偏转角，或利用公式（9）求得允许最小转弯半径。

3.4 管端弯矩

目前顶管管道设计时，对于管道纵向只验算了最大顶力；但通过公式（6），还可以计算管道接头接触面的偏心荷载对管道端部产生的纵向弯矩作用；虽然远离端部的管道截面除了承受这个弯矩，还会承受由于管道转弯引起的管侧不平衡土压力所产生的纵向弯矩；但在端部附近的范围内，这也是顶管管道截面面积相对小的位置，管道承受的纵向弯矩是可以按公式（6）计算的，这样就可以按偏压构件进行管道的纵向承载力验算，或计算管道的纵向钢筋。

当1＜λ时，κ2＝π（1-β4）/64λ；当0＜λ＜1时，解析公式较复杂，除了按表2计算，也可以查图7得到。

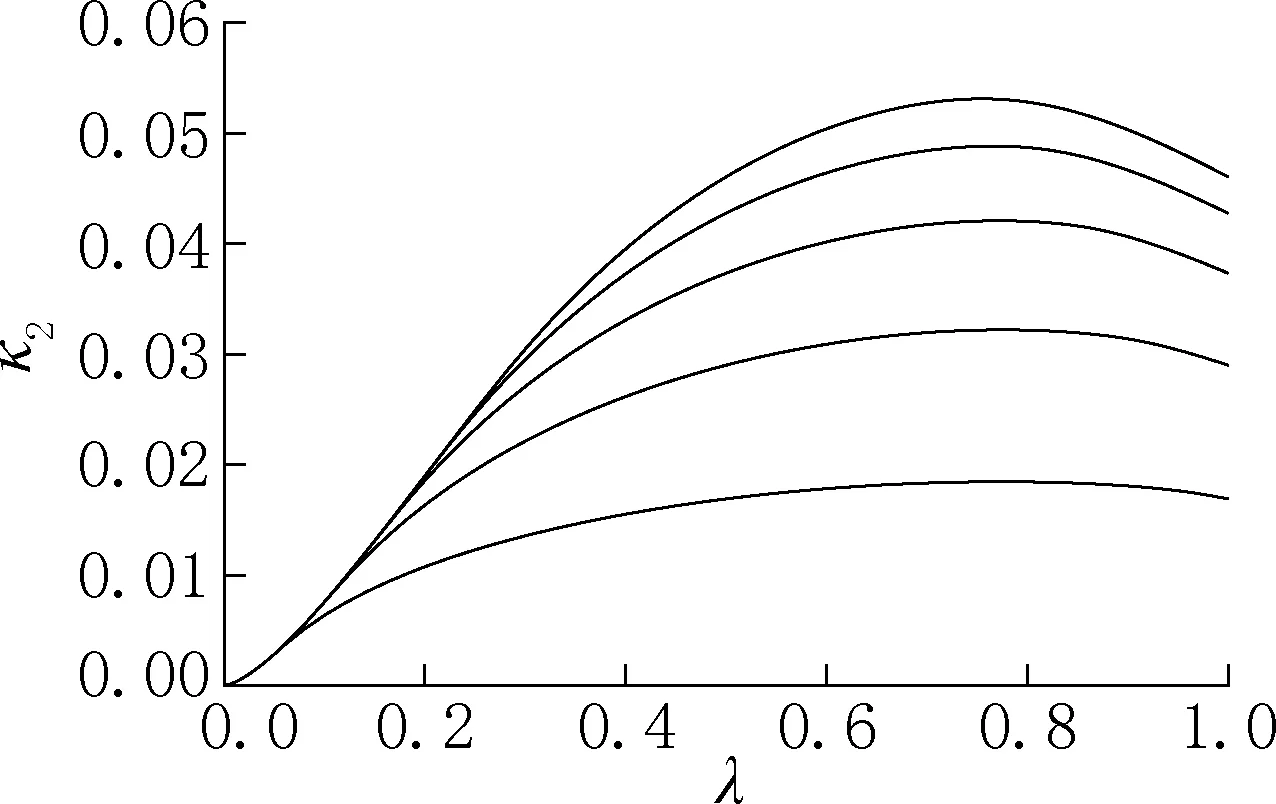
图7 弯矩系数κ2与λ的关系Fig.7 Relationship of the moment coefficient κ2and λ

对于顶管管道纵向弯矩的分布，后续可作进一步研究。

4 对截面压应力分布形态的讨论

以上公式全部建立在接头处压应力为线性分布的假定之上，这要求管道和垫板材料的弹性模量为常量，而Scherle（1983）［3］通过试验指出：适合做垫板的松木板和粘合板的弹性模量随着压应力增大而线性增大；对于松木，压应力为20MPa→60MPa时，弹性模量为30MPa→90MPa；对于粘合板，压应力为0MPa→60MPa时，弹性模量为40MPa→130MPa。这意味着接头处压应力分布不是线性的，而可能是二次方分布的。目前ASCE27［2］和CECS246［1］都是采用线性分布模型，而德国规范《Statische Berechnung von Vortriebsrohren：Arbeitsblatt》DWA-A161［4］要求有木垫板时采用二次方分布，没有垫板时采用线性分布。

4.1 接头截面压应力二次方分布条件下的解析公式

采用第1节相同的方法可推导解析公式如下，其中各参数定义和第1节相同，但以η1、η2、η3分别表示合力系数、力矩系数和合力偏心距系数，η1、η2取值分别见表3、表4。

表3 合力系数η1Tab.3 Resultant force coefficient η1

表4 力矩系数η2Tab.4 Moment coefficient η2

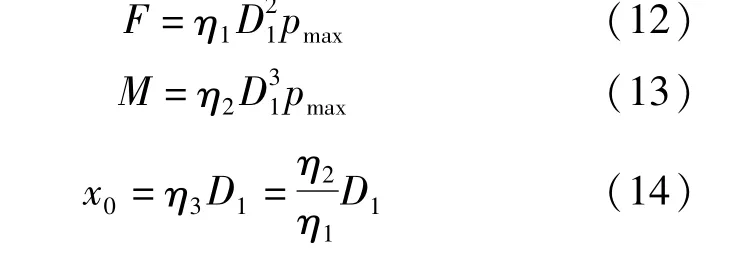
4.2 两种应力分布的对比

限于篇幅，本文仅作简单对比，结论如下：

（1）对于相同的λ，β在0.5～0.9范围内时，η1约为κ1的60%～70%。

（2）对于相同的λ，当λ＜1时，η2＜κ2；当λ＞1时，η2＞κ2；λ＝1时，η2＝κ2＝-（1-β4）π/64；κ2约在λ＝0.75～0.8时最大，η2在λ＝1时最大。

5 结论

1.基于顶管接头接触面压应力为线性分布的假定，以管道接头接触面受压区间比和内外径比为基础变量，可推导顶力合力、力矩和偏心距的解析公式。

2.由顶管接头的变形约束条件，可推导受压区间比基于管道偏转角、管线转弯半径的解析公式，以及顶管接头允许最大偏转角。

3.在上面两步骤的基础上，就可以基于受压区间比、顶力合力偏心距、管道偏转角、管线转弯半径这四个变量之一计算允许最大顶力，或由已知施工顶力计算允许最大偏心距、允许最大偏转角或允许最小转弯半径。

4.为方便应用，根据解析公式绘制了偏心折减系数关于受压区间比、顶力合力偏心距的图表供查询使用。

5.由偏心顶力对管端截面的力矩解析公式，可以对管端截面的纵向承载力进行计算，后续可根据管道偏转时管侧土压分布，对偏心状态下管道纵向弯矩分布进行研究。

6.根据Scherle（1983）［3］的研究，假定顶管接头接触面压应力为二次方分布，本文推导了顶力合力、力矩和偏心距的解析公式。两种假定条件下的计算结果相差较大，需要后续作进一步试验研究确定哪种应力分布模型更符合实际情况。