精益生产模式下的供应商评价Fuzzy-AHP模型

张顺堂,魏雪梦

(山东工商学院 管理科学与工程学院,山东 烟台 264005)

精益生产(Lean Production)起源于日本丰田公司创立的准时制拉动式生产体系,也叫丰田生产方式,倡导以人为本、持续改进、追求零浪费和零库存。通过实施精益生产,消除浪费,提升质量和效率,增强企业竞争优势。在此之前,企业主要采用大批量推动式生产,因不能以销定产,便产生库存堆积,导致资源浪费。至此,企业开始寻找一种能够消除浪费,降低成本的生产模式,精益生产应运而生。其核心思想是利用全员改善,消除浪费,追求企业的长期绩效。在精细供应链中,准时化生产具有降低供应链成本的作用;龙昀光,潘杰义等采用层级回归模型得出精益生产对制造业的经济环境、社会绩效具有正向促进作用;精益设计的提出,使精益生产进一步发展[1-8]。

考虑到产业的经济环境因素,精益运营需要在产业链上进行供应链深度拓展及合作,结合产业链的发展特点,整合产业链上下游资源,对产业链上的企业进行融资、信息、进出口服务、结算、仓储、物流、配送、交易撮合等系列服务,形成闭环的信息共享、资源共享、运作协同的价值链,其中供应商占据关键因素[9]。本文通过在精益生产方式下建立评价模型,优选供应商,这将极大促进产业生态供应链的形成,并为企业决策提供全面的信息。

一、面向精益生产的供应商评价体系的建立

精益生产强调“多品种小批量柔性生产”和“准时制生产”。在产业生态供应链上,企业同时追求经济效益和生态效益,利用精益思想改进供应链绩效,促使双方运营协同,使得经济效益最大化;建立精益供应链的整体优化模型和求解方法,增强竞争力,促进可持续发展。在精益生产方式下,学者从不同角度对指标体系的影响因素进行分析[10-14]。本文在精益生产方式下,将供应商选择的影响因素分为4个方面:

1.生产能力。精益供应对应于拉动式生产,采用订单驱动的方式满足客户需求。当企业收到订单时,利用生产看板,将信息逐步向前一道工序传递,直到工序的最前端,驱动整个供应链运作起来,供应商用最快速度、最低成本满足顾客需求。

2.服务。精益生产实现消除浪费的关键在于准时制生产,要求供应商准时供货,提供使顾客满意的服务。服务是供应商的软件部分,企业不仅关注供应商生产能力,还关注交货能力、售后服务及订货提前期等这些因素[15],这些因素影响着企业能否按时交货,是否耽误生产计划及生产进度,企业的生产计划与控制需要与供应商协同推进。

3.发展战略。在精益生产方式下,企业将供应商视为长期合作伙伴,用长远眼光评价供应商发展,综合考虑供应商的研究开发能力、人才引进能力、企业合作能力、财务状况以及生产设备、供应商是否重视新产品的开发、是否有自己的研发团队等,必要时,需要与供应商建立合作发展组织,协助供应商成长与发展。

4.外部环境。实施精益生产可降低或消除供应链各环节不必要的成本与浪费,利用快速换模技术及全员设备维护方法等实现精益供应的柔性以及敏捷性。在选择供应商时,不仅考虑供应商本身的内部因素,还要考虑供应商所处的地理位置、政治、文化环境等。综上所述,基于精益生产的供应商指标体系模型如图1所示。

图1 供应商指标体系模型

该结构模型将指标体系分为四部分。目标层主要建立供应商评价体系,系统地考虑指标要素;生产能力、服务、发展战略及外部环境属于准则层,为实现预订目标所设定的中间环节;指标层包含22个评价指标,综合分析影响供应商选择的主要因素;方案层是选择三家供应商对评价体系进行验证,检验其有效性。

二、层次分析法

层次分析法的基本原理是:构建一个层次结构模型,利用较少定量信息,把决策的思维过程数学化,从而为求解多目标的复杂决策问题提供简便方法。李延平提出多品种分批次采购供应商选择的多层次决策模型并利用蚁群算法进行求解;李春好,李薇等基于SW判断模式和多属性决策属性价值公度方法提出了ToAHP目标导向层次分析法[16-20]。

层次分析法的一般步骤为:

1.构造层次分析模型。构建供应商的评价指标体系,确定目标层、准则层和指标层。

2.构造判断矩阵。将两两元素进行比较,得出判断矩阵,根据比率标度将矩阵定量化,常用的1～9标度方法如下[21]。

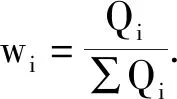
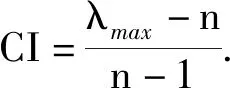
当随机一致性比率CR=CI/RI〈0.1 时,则认为结构符合一致性,其1～9阶RI取值如表所示。

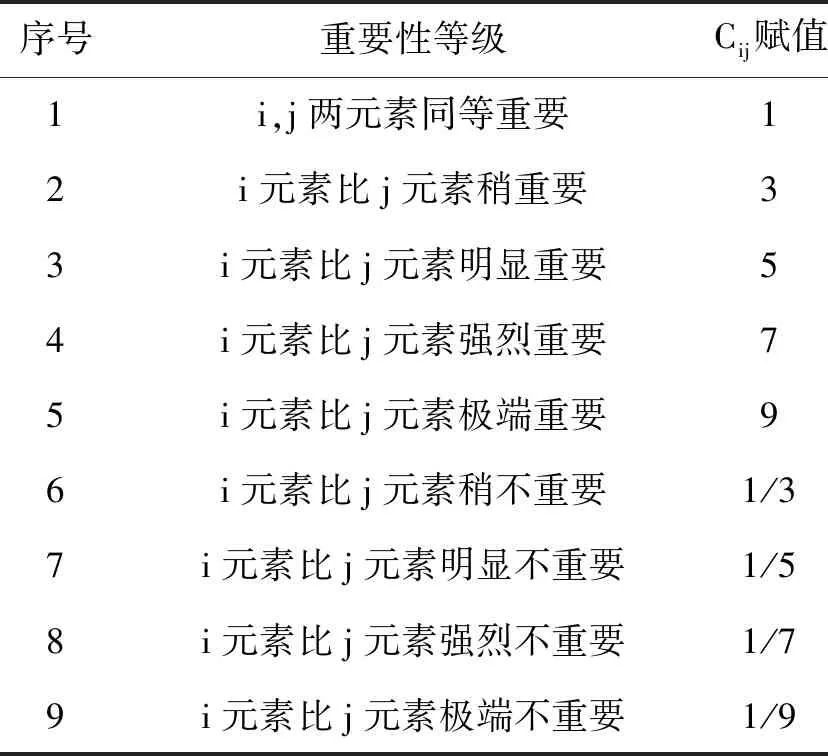
表1 判断矩阵标度及含义

表2 平均随机一致性指标

4.层次总排序。计算各层元素对系统目标的合成权重。

三、模糊综合评价模型

模糊综合评价是利用模糊数学思想,将一些不易定量的因素定量化,采用隶属度等级状况对被评价事物进行评价。将模糊评价的思想运用到精益生产中,有助于改善企业情况[22-24]。模糊综合评价法一般步骤如下。

1.确定因素集。假设一共有n个一级评价指标u={u1,u2,…,un},每个一级指标中含有多个二级指标,表示为ui={ui1,ui2,…,uin},i=1,2,…,s,且同时满足 n1+n2+…+ns=n,U1∪U2∪…∪US=U,对任意的i≠j,Ui∩Uj=Φ.

2.确定评语集。v={v1,v2,…,vn}表示每种因素所处状态的n种决断(即评价等级)。

3.构造权重向量。权重向量用W表示,即w=(w1,w2…,wm),其中wi>0,且∑wi=1,本文用层次分析法确定指标权重。

4.构造模糊评判矩阵。对因素集Ui作综合评判,记Ri为单因素评判矩阵,得到一级评判向量:Bi=Ai∘Ri=(bi1,bi2,…,bim),i=1,2,…,s。将Ui看作一个因素,记作:K={u1,u2,…,us},得到K的单因素评判矩阵:

每个Ui作为U的一部分,得出二级评判矩阵:B=A∘R=(b1,b2,…,bm),其中,符号“∘”表示广义的合成运算。

5.评价指标处理。得到决策集B之后采用模糊分布法,对上述决策集B进行归一化处理得到B′,根据最大隶属度分析评判结果。

四、实例分析

M公司是一家实施精益生产下的汽车零部件制造型企业,主要生产流程是从供应商处采购不同汽车型号零部件的毛坯件,对其进行弯管、抛光、电镀、焊接和包装销售。公司订单特点是多品种小批量,公司经营战略要求利用精益思想实施准时化拉动式生产,力求达到库存最小的情况下又能满足发货需求,本文以该公司为研究对象,从生产能力、服务、发展战略和外部环境4个方面来分析指标体系,并对3家供应商进行评价,验证指标体系有效性。

1.层次分析法求解指标权重。根据层次分析法确定评价指标构造判断矩阵,数据来源于公司有关部门的专家对指标重要程度进行打分,根据建立的指标模型,确定A-B判断矩阵如表所示。

在MATLAB中输入以下命令,执行软件得出判断矩阵的特征值及特征向量。

A=[1 3 4 6;1/3 1 2 4;1/4 1/2 1 2;1/6 1/4 1/2 1]

[V,q]=eig(A)

根据输出结果,最大特征值λmax=4.05,其特征值所对应的特征向量为QA=(0.89,0.39,0.21,0.11)T.

对特征向量进行归一化处理得wA=(0.56,0.24,0.13,0.07)T.

符合一致性检验。准则层相对于目标层的权重向量为wA=(0.56,0.24,0.13,0.07)T.

采用同样的方法依次计算出B1-C,B2-C,B3-C,B4-C的判断矩阵。

表3 总目标层的A-B判断矩阵

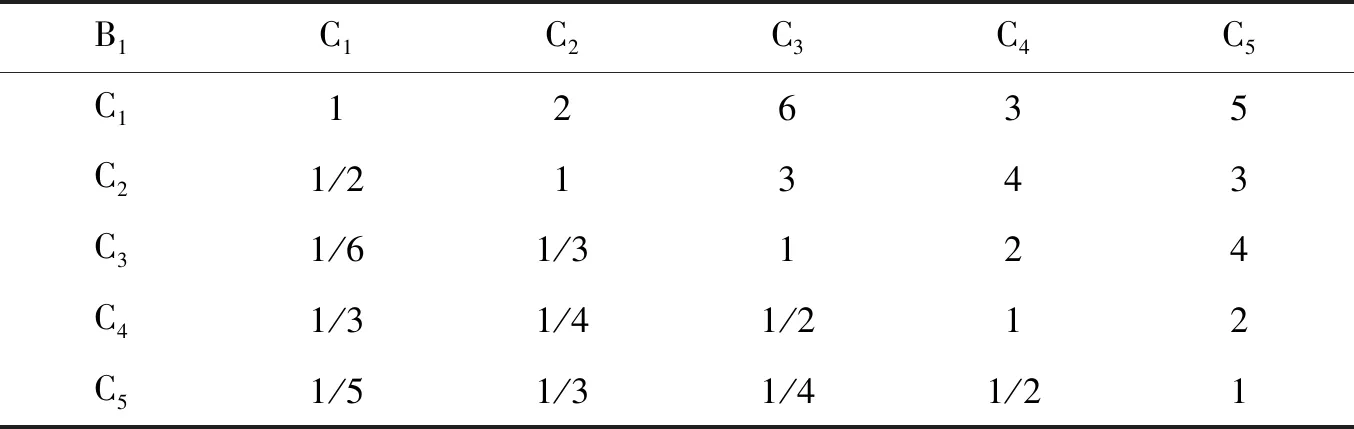
表4 产品B1-C的判断矩阵

根据输出结果知最大特征值λmax=5.35,其特征值所对应的特征向量为QB1=(0.81,0.49,0.25,0.17,0.11)T.

对特征向量进行归一化处理得wB1=(0.44,0.27,0.14,0.09,0.06)T.

符合一致性检验。指标层相对于准则层的权重向量为wB1=(0.44,0.27,0.14,0.09,0.06)T.

根据输出结果得到λmax=6.46,其特征值所对应的特征向量为QB2=(0.77,0.42,0.32,0.27,0.2,0.14)T.

表5 服务B2-C的判断矩阵

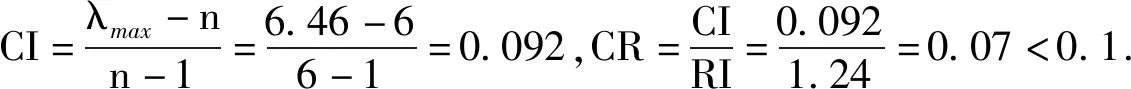
符合一致性检验。指标层相对于准则层的权重向量为wB2=(0.36,0.2,0.15,0.13,0.09,0.07)T.

符合一致性检验。指标层相对于准则层的权重向量为wB3=(0.36,0.25,0.21,0.12,0.07)T.

表6 发展战略B3-C的判断矩阵

表7 外部环境B4-C的判断矩阵

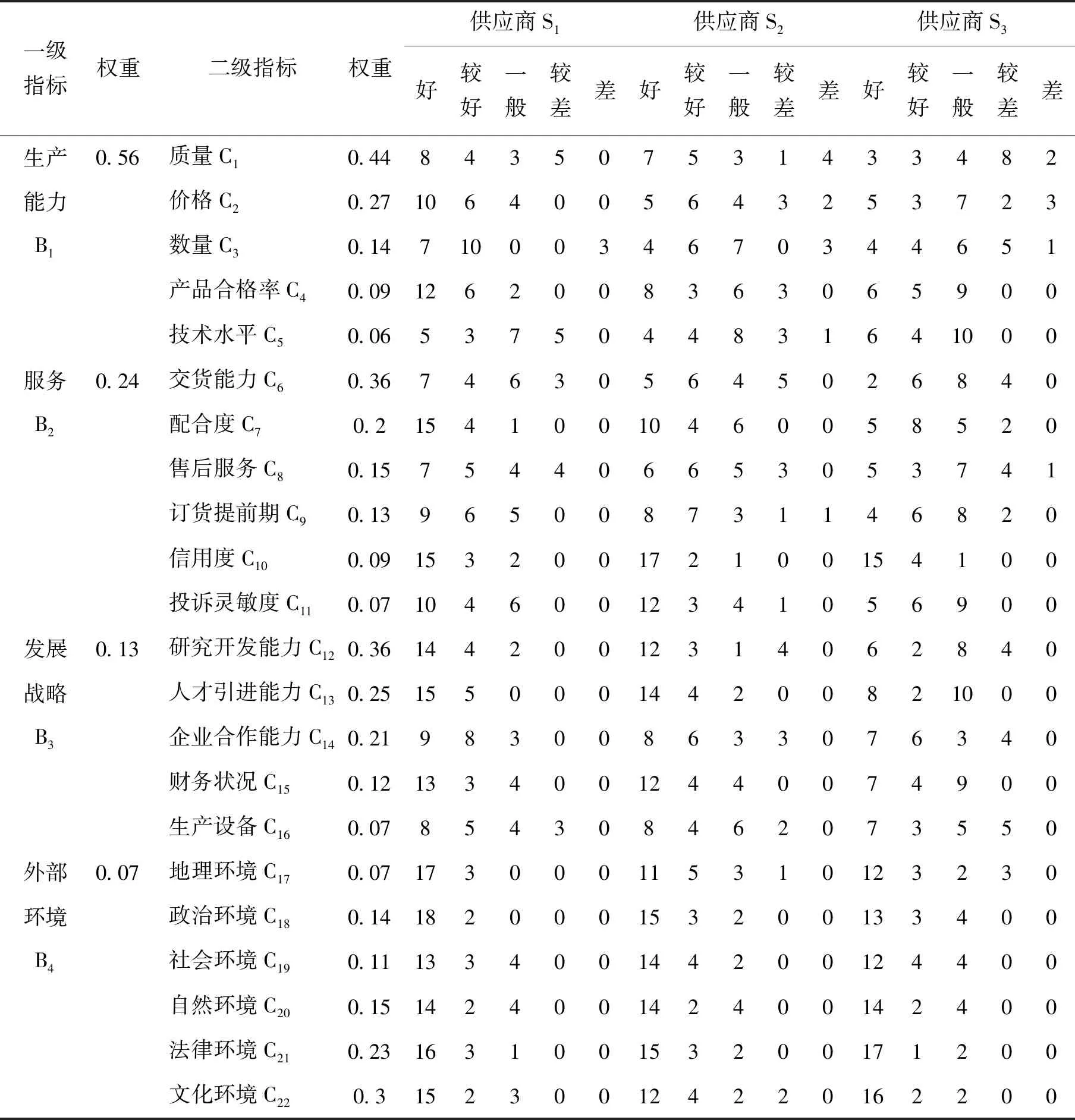
表8 专家打分成绩表

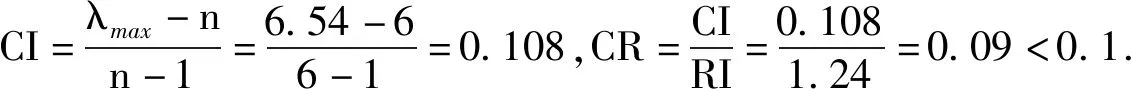
符合一致性检验。指标层相对于准则层的权重向量为wB4=(0.07,0.14,0.11,0.15,0.23,0.3)T.

最后,计算得出层次单排序及各级指标权重,对数据进行综合排序,如表8所示。

2.模糊综合评价。首先,建立因素集。使用层次分析法求出权重向量后,用模糊综合评价法确定评价因素和评价等级。评价指标集分为两个层次:第一层:准则层u=(B1,B2,B3,B4);第二层:指标层B1=(C1,C2,C3,C4,C5);B2=(C6,C7,C8,C9,C10,C11);B3=(C12,C13,C14,C15,C16);B4=(C17,C18,C19,C20,C21,C22).其次,建立评语集。把评价等级主要分为5个等级,分别为优、良、中、一般、差,即v={v1,v2,…,vn}={优，良，中，一般，差}。再次,构造评判矩阵及模糊合成。现聘请20位专家组成评审团对供应商S1,S2,S3进行评价,以问卷调查的形式对评价指标体系进行综合评价,由此可以得到打分成绩如表所示。

根据专家得分结果,对供应商S1得分进行归一化、标准化处理得BB1=wB1∘RB1=(0.429,0.266,0.15,0.125,0.021),BB2=wB2∘RB2=(0.4895,0.216,0.2105,0.084,0),BB3=wB3∘RB3=(0.6555,0.2765,0.078,0,0),

BB4=wB4∘RB4=(0.771,0.1205,0.1085,0,0).

其次,二级综合评判为

=(0.4969,0.2452,0.1523,0.0902,0.0118),归一化处理得到B′=(0.4987,0.2461,0.1529,0.0905,0.0118).

根据最大隶属度原则,说明该供应商评价结果为优。采用同样方法,依次评价供应商S2,S3,得出结果如表。

根据表9可以得出,供应商S1,S2的评价结果为好,S3的评价结果为一般,所以供应商S1,S2优于S3。

根据精益生产建立评价模型,在考虑质量、价格等因素的基础上,同时考虑供应商能提供产品的数量上限、交货能力及信用度等,使得在精益生产模式下选择供应商具有更加全面的科学依据,有助于企业在生态供应链中推行精益生产方式理念。通过使用模糊层次综合评价法,把定性评价转化为定量评价,避免了主观性和人为原因而导致的误差,使评价结果更具有合理性。同时产业生态供应链强调物质在供应链内循环流动形成“闭合回路”,使物料达到100%的利用率,对环境无危害,更加关注环境的重要性。但本文建立的模型存在一定的劣势,即当指标过多时,数据统计量大且权重不易确定,存在一定的局限性。

表9 供应商评价结果