风电与多能源储能联合调峰多场景动态鲁棒优化模型
2020-05-19万玉良吴晓丹顾大可王泽镝
万玉良, 刘 鑫, 吴晓丹, 顾大可, 王泽镝
(1.国网内蒙古东部电力有限公司, 内蒙古 呼和浩特 010000; 2.东北电力大学,吉林 吉林 132012; 3.沈阳工业大学, 辽宁 沈阳 110870)
0 前言
具有波动性与不确定性的风电大规模入网,会给电网调峰带来巨大挑战[1]~[3]。为应对高比例风电入网所导致的调峰难问题, 功率响应速率快、效率高的电池储能系统已成为一种重要的调峰资源[4],[5]。 但是,从电池储能系统高建设成本、“三北地区”弃风和冬季供暖需求考虑,电池储能系统建设规模仍受限制[6]。 因此,考虑电池储能与电锅炉协调运行的多源储能系统优化,是解决大规模风电并网后调峰问题的有效途径。
针对大规模风电并网后的大量弃风及电网调峰困难的问题,为提高风光储运行效率,文献[7]通过电池组SOC 特性分析,提出了电池模块化运行的优化模型。 为抑制风电波动,提高电网稳定性,文献[8]提出考虑频率响应的大规模电池储能系统并网控制策略。 为提高风电消纳能力,考虑调峰、风电消纳等多方面收益,文献[9]提出一种电池储能的容量优化配置模型。 文献[10]为平抑风电波动,考虑锂电池与超级电容的优势互补,提出了考虑超级电容的锂电池功率分配策略。
以上研究虽然在一定程度上解决了调峰问题,但未能深入考虑在风电不确性和调峰多场景下的多能源储能优化运行。 基于此,本文考虑了风电波动下的调峰多场景划分,建立了风电与电热多源协调储能鲁棒优化模型。
1 电热多能源储能系统模型
本文考虑多源协调优化运行,利用电池储能与电锅炉及储热装置构建了电热多源储能系统(E-HMESS), 配合风电协调运行进行调峰。E-HMESS 的拓扑结构如图1 所示[11]。
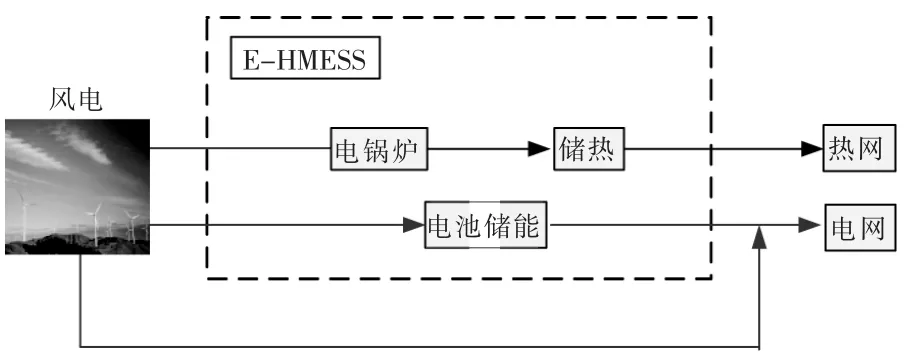
图1 E-HMESS 拓扑结构Fig.1 The topology of E-HMESS
1.1 电池模型
电池储能系统通过电能的存储与释放进行削峰填谷,其容量与储放功率关系如下:

式中:Ees(t)为 t 时刻电池容量;Pes(t),Peo(t)分别为t 时刻电池储、放功率;ηes,ηeo分别为电池储、放效率;Δt 为运行时段。
1.2 电锅炉模型
电锅炉可将风电转为热能进行供暖, 当存在大规模弃风电量时可以提供一定调峰容量,其电热转换模型为
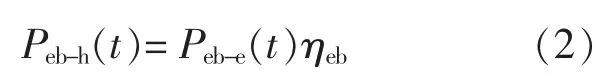
式中:Peb-h(t),Peb-e(t)分别为电锅炉制热、耗电功率;ηeb为电热转换效率。
1.3 储热模型
电锅炉实现电制热后, 可利用储热罐存储热能,为电网提供更多的调峰容量,其储热模型为
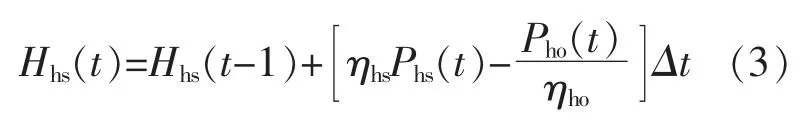
式中:Hhs(t)为 t 时刻的储热容量;Phs(t),Pho(t)分别为 t 时刻储热的储、放功率;ηhs,ηho分别为储热装置的储、放效率。
2 考虑风电波动的调峰多场景划分下的鲁棒运行模式
2.1 调峰多场景划分
针对大规模风电的高不确定性特点,在风电与E-HMESS 协调运行前, 基于研究周期内的N条风电曲线, 根据E-HMESS 容量对调峰需求的影响划分调峰场景。
(1)场景一
场景一为风电低出力时的调峰场景, 即系统中电负荷出现峰值且处于风电低出力, 须要E-HMES 协调运行供电。
①给出可信基准 α1, 选取风电曲线 Pw(K1),定义超过 α1的风电出力 Pwb-H的最小基准为Pwb-H(K1),Pw(K1)组成的集合为 PwΩ1,风电日均出力最大曲线为Pm1。
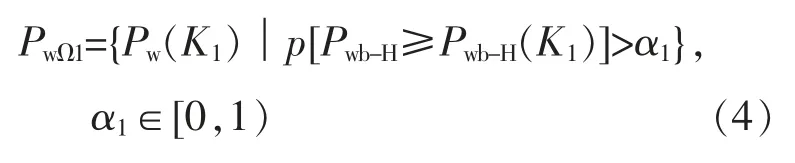
②考虑在场景一的情况下E-HMESS 的供电可信度。 E-HMESS 须具有一定电量备用,进而给出可信基准 β1。 从 PwΩ1中选出曲线保证Pwb-H(K1)不大于的概率超过 β1。构成的集合为中最大风电出力曲线为Pn1。
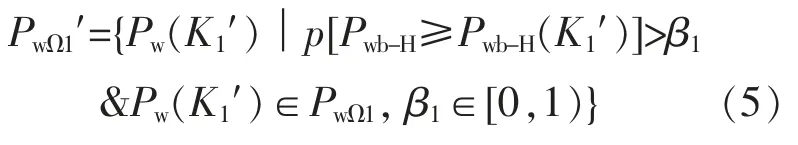
③确定可信基准为α1的情况下, 场景一Pw1及其概率pw1为
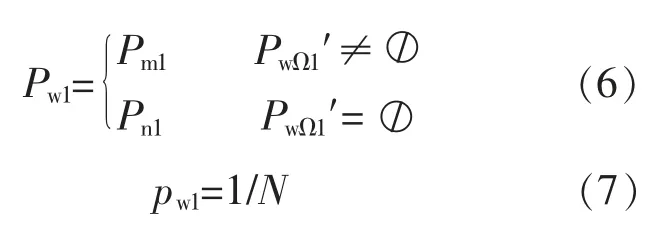
(2)场景二
场景二为风电高出力时的调峰场景, 即系统中电负荷出现峰值且风电处于高出力, 需要E-HMESS 协调运行储电。
①给出可信基准 α2, 选取风电曲线 Pw(K2),定义超过 α1的风电出力 Pwb-L的最大基准为Pwb-L(K2),Pw(K2)组成的集合为 PwΩ2,风电日均出力最大曲线为Pm2。
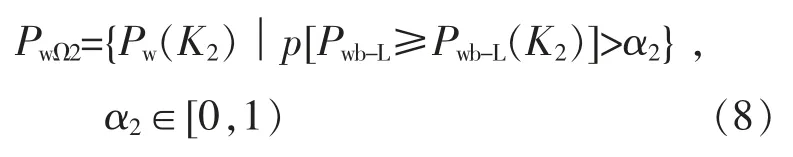
②考虑在场景二情况下E-HMESS 的储电可信度,E-HMESS 须具有一定电量存储裕度。 从PwΩ2中选出满足E-HMESS 容量能够存储最大的风电曲线 PwΩ2′, 则 PwΩ2′中最小风电出力曲线为Pn2。
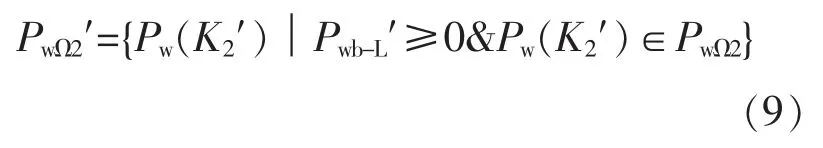
③确定可信基准为α2的情况下,Pw2及其概率pw2为

在风电与E-HMESS 协同调峰运行中, 考虑两个场景进行优化, 通过电池与电储热的协调运行来保证系统运行可靠性, 也可反映出系统的调峰需求。
2.2 E-HMESS多场景鲁棒运行模式
基于对风电与E-HMESS 协调运行的调峰多场景划分,图2 给出调峰多场景下E-HMESS的鲁棒运行模式和鲁棒储放优化轨迹, 保证E-HMESS 在Δt 时段内实现多场景间的储放电过渡。
Δt 时段E-HMESS 储电放电范围为
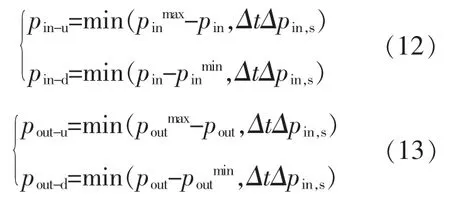

图2 E-HMESS 鲁棒运行轨迹Fig 2 The robust trajectory of E-HMESS
式中:pin-u,pin-d,pout-u,pout-d分别为 E-HMESS 在 Δt时段可提供电能储、放裕度;pin,pout分别为E-HMESS 电能储、 放功率;pinmax,pinmin,poutmax,poutmin分别为 E-HMESS 储、电放电出力的上、下限;Δpin,s,Δpout,s分别为 E-HMESS 储、放的最大速率。
由图2 可知, 鲁棒运行点可根据风电波动及电网调节需求,在不同场景下切换运行方式,与风电协调运行, 灵活调峰。 此模式可在大规模弃风时,通过电池和电锅炉的协调来消纳风电,在电负荷峰值时供电,缓解调峰压力,实现风电利用最大化。 E-HMESS 比传统调峰机组的灵活性更高。
3 电-热多源协调储能鲁棒优化模型
3.1 目标函数
针对本文提出的调峰多场景及鲁棒运行模式,建立风电利用最大化下的E-HMESS 调峰运行成本最低的鲁棒优化模型。 该模型主要考虑E-HMESS 运行成本,以弃风电量最小为目标。
(1)E-HMESS 运行成本最小目标
运行成本最小目标:
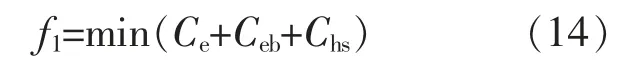
式中:Ce,Ceb,Chs分别为电池、电锅炉、储热的运行成本。

式中:Ce,r,Ceb,r分别为电池储能、 电锅炉的运行成本系数;Chs,r为储热装置的维护成本系数;Pe(t),Phs(t)分别为电池和储热装置在t 时刻的电、热储放功率,正为储,负为放;Peb(t)为电锅炉在 t 时刻的耗电功率;NT为E-HMESS 的运行总时段。
(2)弃风最小目标
弃风电量为风电预测与并网功率之差:
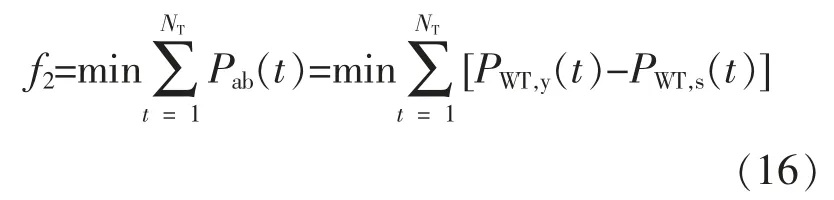
式中:Pab(t)为 t 时段的弃风功率值;PWT,y(t)为 t 时段风电预测值;PWT,s(t)为 t 时段风电实发功率值。
3.2 多场景鲁棒约束
本文建立多场景下风电与E-HMESS 协调调峰的鲁棒可行域 Ω(α,μ,υ,S),除了对传统的等式与不等式加以约束, 还考虑在多场景下公式(12),(13)中 E-HMESS 的储放范围。Ω(α,μ,υ,S)为

式中:qin(s),qout(s)分别为 pin,pout的自适应变量,根据场景 s 的切换而变;Γ(α,μ,υ,S)为场景 s 下解的存在条件。
式(17)表示至少存在一组解{pin,pout,qin(s),qout(s)}满足 Γ(α,μ,υ,S)。Γ(α,μ,υ,S)由如下鲁棒约束条件给出。
多源调峰系统功率平衡鲁棒约束:
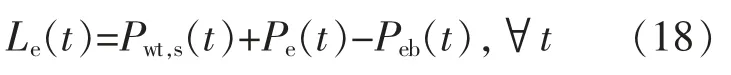
式中:Le(t)为 t 时刻电负荷需求。
E-HMESS 鲁棒约束:
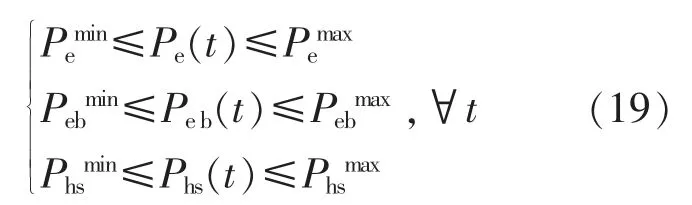
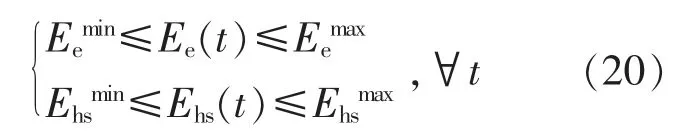
考虑多场景风电与E-HMESS 调峰时间尺度鲁棒约束,qin(s),qout(s)须满足 E-HMESS 在 Δt 时间尺度下的调节范围。
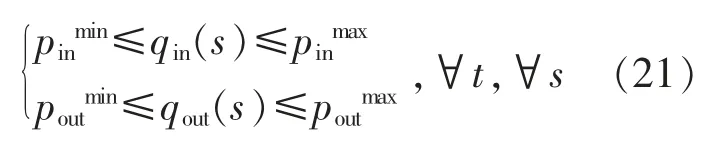
3.3 求解
针对本文的多目标优化模型, 采用多目标进化算法求解,实现风电与E-HMESS 调峰多场景鲁棒优化[12]。 多目标进化算法求解过程如图3 所示。
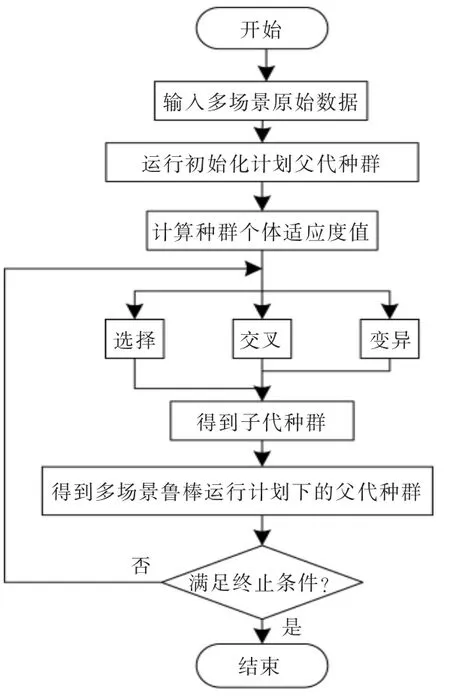
图3 求解流程Fig.3 The flow chart of solution
4 仿真验证
利用某地区配网总用功负荷及风电实际数据,建立电-热多源协调储能鲁棒优化仿真模型。考虑在风电波动下的E-HMESS 多场景调峰优化运行模式, 与采用纯电池储能调峰进行经济性与弃风电量对比。
配网实际总负荷为1 500 MW,风电装机容量为800 MW,配有100 MW 的电池储能系统。 利用本文提出的电-热多源协调储能鲁棒优化模型,考虑大规模消纳弃风与经济运行成本最低, 配置50 MM 的电池储能与100 MW 电锅炉和150 MW的储热装置。风电与负荷曲线及场景划分见图4。
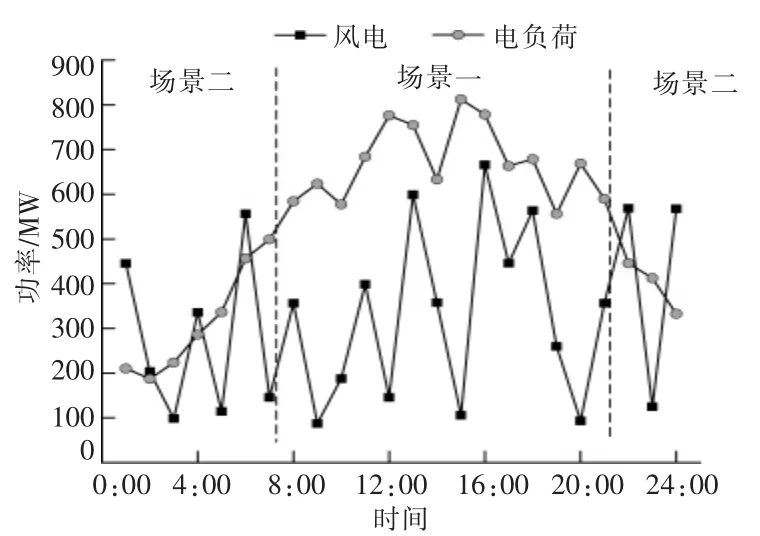
图4 风电与负荷曲线Fig.4 The wind power and load curve
针对如图4 所示的日风电与负荷曲线, 考虑多场景划分及电网调峰需求, 得出如图5 所示的E-HMESS 鲁棒优化运行曲线。
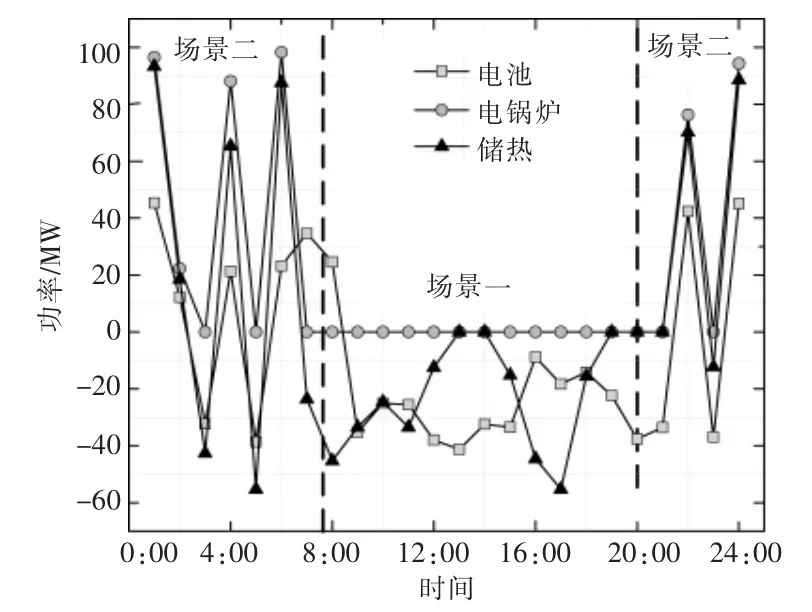
图5 E-HMESS 鲁棒优化运行曲线Fig.5 The robust optimization operation curve of E-HMESS
由图5 可见, 针对大规模风电波动下的电网调峰需求,E-HMESS 在其多场景划分的基础上,可以灵活切换运行方式,实现风电的全利用。在场景一的工况下, 电池、 电锅炉及储热装置协调运行,消纳风电,减少风电弃电量。 在场景二的工况下,电池储能为电网调峰供电,满足电网峰值时的部分需求,储热协调运行进行热能储放。 对比E-HMESS 的鲁棒优化运行与纯电池储能的调峰方式,其运行成本与弃风量如表1 所示。
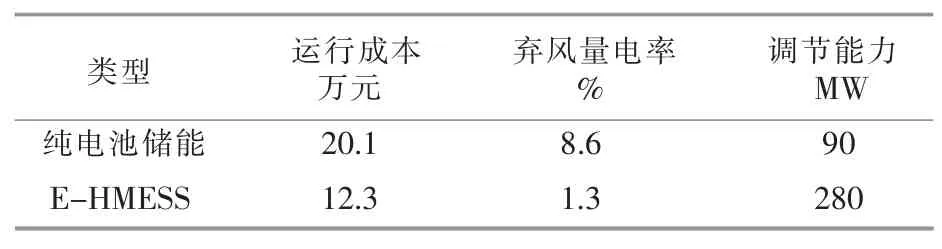
表1 优化对比Table 1 Optimization contrast
由表1 可知,与传统的风储联合调峰相比,本文提出的E-HMESS 鲁棒优化模型在多场景灵活运行的同时, 考虑了电锅炉与储热装置的协调运行,有效地降低运行成本。 在大规模风电波动下,E-HMESS 的弃风电率下降,其调节能力优于纯电池储能。
针对本文多目标鲁棒优化求解,得到Pareto解集图(图 6)。 由图 6 可知,风电与 E-HMESS在联合运行调峰过程中, 弃风电率与运行成本相互制约,若要减少弃风,势必导致运行成本的上升。 因此, 须考虑 E-HMESS 的鲁棒运行模式, 根据实际不同运行场景合理地选择最优调峰方式。

图6 E-HMESS 优化模型Pareto 解集Fig.6 Pareto solution set of E-HMESS optimization model
5 结论
针对火电调峰机组在应对大规模风电波动时调节灵活性低和电池储能系统成本高等问题,提出了考虑电池与电锅炉及储热装置协调的电热多源储能系统, 根据风电波动性及负荷需求划分调峰场景。在此基础上,建立电热多源协调储能的鲁棒优化模型, 并通过仿真算例与电池储能进行对比。
优化结果表明,本文考虑风电工况的调峰多场景划分及E-HMESS 的鲁棒运行方式, 可实现风电利用最大化并满足电网调峰需求。 EHMESS 鲁棒运行模式,可实现多场景下的灵活切换,实现容量配置多时空尺度最优。
与电池储能调峰相比,本文提出的E-HMESS鲁棒优化运行模型,具有更优的运行成本,有效地减少弃风电量。
