基于虚拟阻尼前馈的VSG储能系统功率调频解耦控制策略
2020-05-19杜立群
赵 芳, 杜立群
(1.内蒙古建筑职业技术学院, 内蒙古 呼和浩特 010070; 2.内蒙古农业大学 机电工程学院, 内蒙古呼和浩特 010018)
0 引言
光伏、 风电等可再生能源的输出功率具有间歇性且难以预测[1],其大规模应用给电力系统的可靠运行及优化调度带来了巨大的挑战[2],[3]。
为应对上述问题,风电、光伏配备电池储能系统或区域电网内配置调峰、 调频用储能装置逐渐成为研究热点。 电池储能系统作为一种柔性负荷可根据需求实现功率的吞吐。 文献[4]介绍了一种风电场中储能介质类型的选择方法及容量配置策略。 文献[5]研究了超级电容与电池混合的储能系统在平滑风电出力中的作用。 文献[6]进一步给出了微电网不确定运行下多种介质储能的优化分配原则,提高了储能系统的功率、容量等级。 文献[7]对混合储能系统的配置问题开展了研究, 给出了一种基于混合先进算法的配置策略。 文献[8]研究了级联多电平拓扑结构在大规模储能系统中应用的可能, 并给出了一种模块间电池均衡的调制方法。 虽然储能系统在调节可再生能源稳定运行方面起到了积极作用, 但现有实际应用的并网储能系统多以PQ 源形式运行, 孤岛运行时多采用Vf控制或下垂控制。该传统控制方法由于缺乏惯性,加剧了可再生能源占主导地位的微电网对扰动及故障的抵抗能力,降低了系统运行的可靠性。文献[8]建立了储能系统VSG 控制的宽频带小信号模型,为VSG 虚拟参数的整定提供了参考依据。 文献[9]研究了光储柴一体系统中的虚拟同步发电机控制方法。 文献[10]对双馈异步风力发电机的虚拟同步发电机控制稳定性进行了分析, 讨论了不同场景下虚拟惯性时间常数和虚拟阻尼对小干扰稳定的影响。文献[11]对VSG 控制变流器在LC滤波器情况下发生振荡的机理进行了分析并给出了一种抑制方法。 上述文献均建立在同步发电机二阶暂态模型的基础上, 对电网频率存在偏差情况下,VSG 的一次调频特性与阻尼环路存在的有功功率耦合问题并未阐明。 文献[12]通过对有功的指令调节误差积分来消除稳态误差, 并未对一次调频和阻尼回路的耦合问题进行讨论。 文献[13],[14]通过在阻尼反馈回路叠加高通滤波环节,实现了稳态情况下调频与阻尼的解耦,但该方法引入过多参数变量,加剧了VSG 有功环路稳定性分析的难度。
本文提出了一种虚拟阻尼前馈的改进型VSG 控制方法,与传统方案对比,该方法未引入额外变量,且在电网频率存在稳态偏差时,实现了VSG 一次调频特性与阻尼功率环节的解耦,保证了储能系统一次调频的准确性。 最后,在Matlab/Simulink 中搭建的仿真模型, 验证了本文所提策略的可行性及参数分析的有效性。
1 传统VSG控制储能系统的数学模型
本文储能系统控制采用同步发电机的二阶经典模型[13],[14]。 VSG 控制储能系统的整体框图如图1 所示。
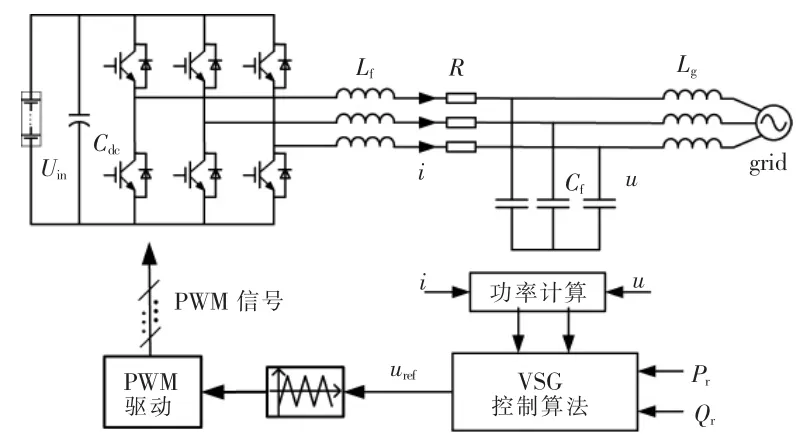
图1 VSG 控制储能系统整体框图Fig.1 Overview of VSG based energy storage system
图中:Uin为储能电池电压;Cdc为直流侧滤波电容;Lf,Lg分别为 LC 滤波器电感、 并网线路电感;R 为并网线路上寄生电阻;Cf为LC 滤波器的滤波电容。
参考同步发电机的转子运动方程,得出VSG有功控制表达式为
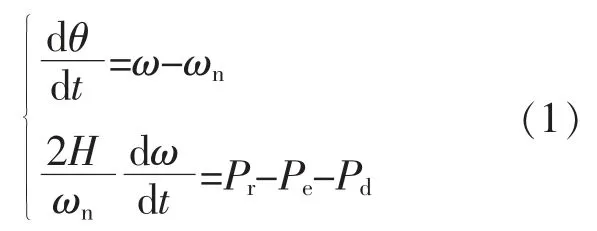
式中:θ,ω 分别为 VSG 虚拟转子的功角、角速度;ωn为额定角速度;Pr,Pe和 Pd分别为 VSG 控制中的给定功率参考、虚拟电磁功率和虚拟阻尼功率;H 为VSG 转子的虚拟惯性时间常数。
为实现储能系统的一次频率调节功能, 本文采用P-f 下垂环节进行模拟,其表达式为
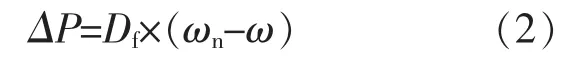
式中:ΔP 为一次调频有功增量;Df为一次调频下垂系数。
根据式(1),(2),可得本文储能系统 VSG 控制的有功控制框图,如图2 所示。
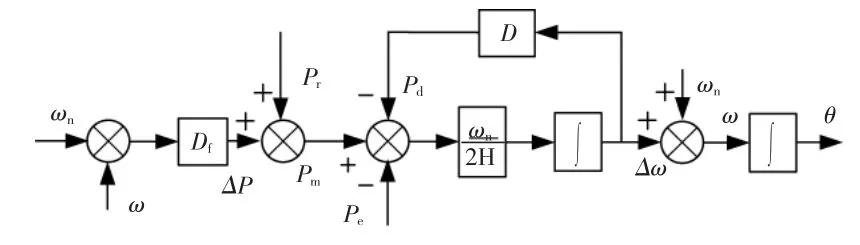
图2 VSG 有功功率控制框图Fig.2 VSG active power of the control diagram
对于模拟同步发电机的一次电压调节特性,本文采用Q-U 下垂控制。 无功控制环路表达式:
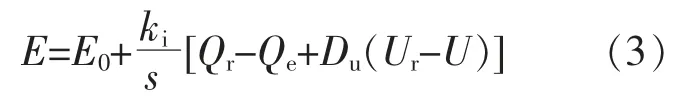
式中:E0为稳态虚拟电势;Qr和 Qe分别为 VSG 无功参考及输出无功功率;Ur为储能系统输出电压幅值参考;Du为一次电压调节下垂系数;ki为虚拟励磁系数。
VSG 无功功率控制框图如图3 所示。
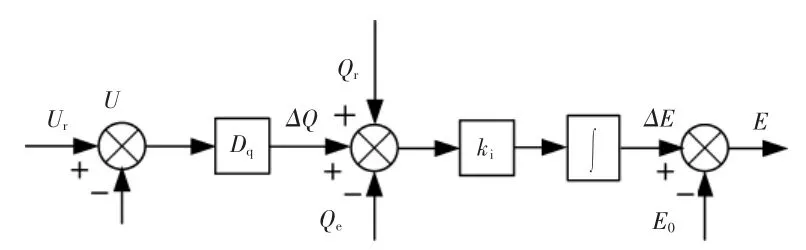
图3 VSG 无功功率控制框图Fig.3 VSG reactive power of the control diagram
2 VSG一次调频与阻尼环路耦合机理分析
根据VSG 有功功率控制结构,得出传统VSG有功闭环控制框图,如图4 所示。
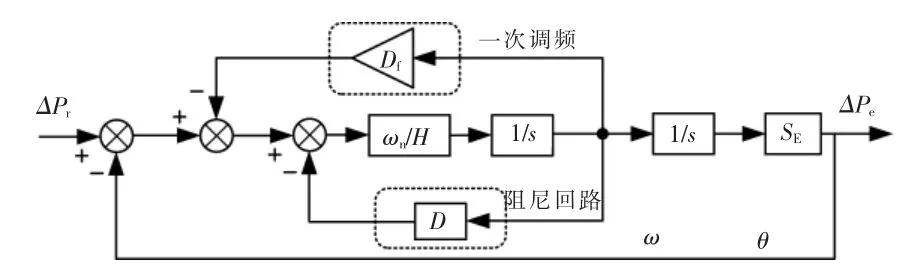
图4 传统VSG 有功回路控制框图Fig.4 Closed-loop control block of active power control
图中SE为VSG 最大输出有功功率, 其表达式为

式中:X 为储能系统至电网的线路阻抗,本文忽略了线路寄生电阻对电网的影响;θ0为额定功率输出时的虚拟功角。
根据图4, 可推导出扰动时储能系统输出有功功率增量的频域表达式为
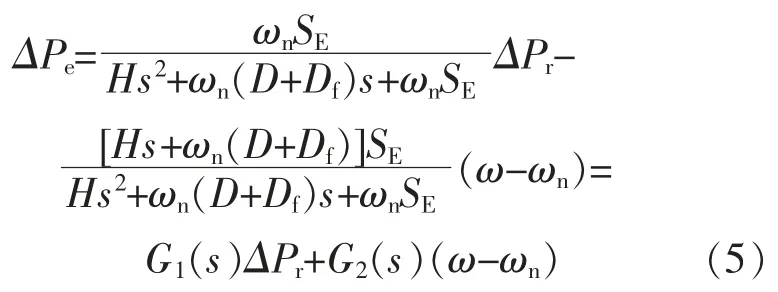
式中:G1(s)和 G2(s)分别为 VSG 功率指令波动和频率扰动至输出有功功率的闭环传递函数。
由式(5)可以看出,输出功率受VSG 功率指令及电网频率波动的影响。 稳态时输出功率增量表达式为
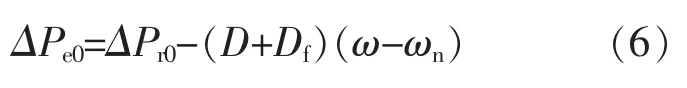
传统VSG 中,不同阻尼系数对一次调频的影响,如图5 所示。

图5 传统VSG 有功环路闭环传递函数阶跃响应Fig.5 Step response of traditional close-loop transfer function of VSG
由式(6)和图5 可知,当电网频率存在偏差,且在稳态的情况下,VSG 输出有功功率的一次调频特性与虚拟阻尼环节存在耦合关系,即VSG 虚拟阻尼特性影响了一次频率调节的精准度。 当系统中存在多机并联运行时, 该问题会严重导致各储能单元输出功率的不匹配。 针对此问题, 文献[13]提出了暂态阻尼概念,使得阻尼环节仅在扰动过程中起到增强稳定性的作用, 而不影响系统稳定情况下的频率调节。 该方法在有功环路中引入了一个额外参数,提高了参数整定难度。
本文提出虚拟阻尼前馈的改进型VSG 控制策略,如图6 所示。
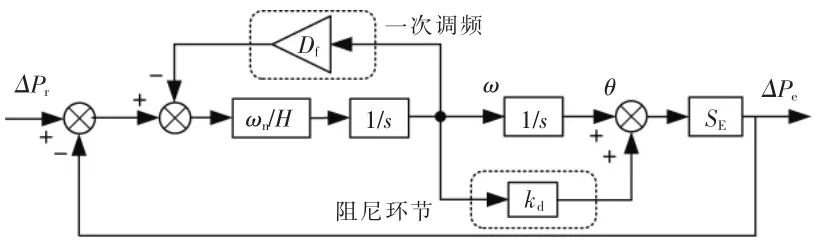
图6 改进VSG 有功闭环控制框图Fig.6 Improved VSG active power control loop based on feedforward damping term
由图6 得到本文所提虚拟阻尼环路前馈后系统的闭环传递函数表达式为
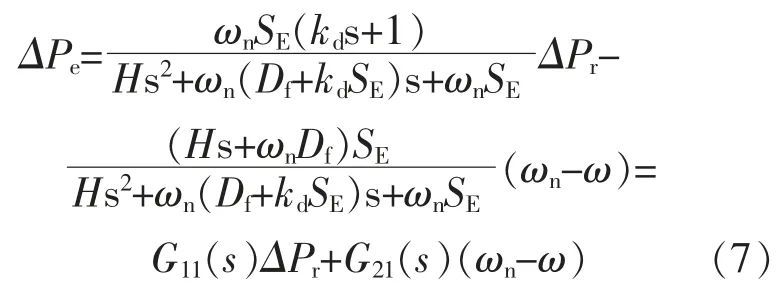
根据终值定理可知, 稳态情况下储能系统输出功率增量表达式为
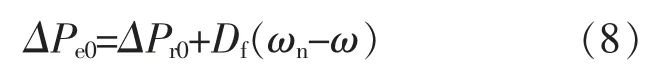
由式(8)可以看出,有功增量为参考指令增量与一次频率调节功率增量之和。对比式(6)可以看出,此时VSG 有功环路中的一次调频特性与阻尼特性实现了功率解耦,VSG 达到了一次调频无稳态误差功率输出。
同样,根据式(8),得出改进后VSG 有功环路控制闭环传递函数的阶跃响应,如图7 所示。除前馈阻尼系数,其余参数与图5 保持一致。
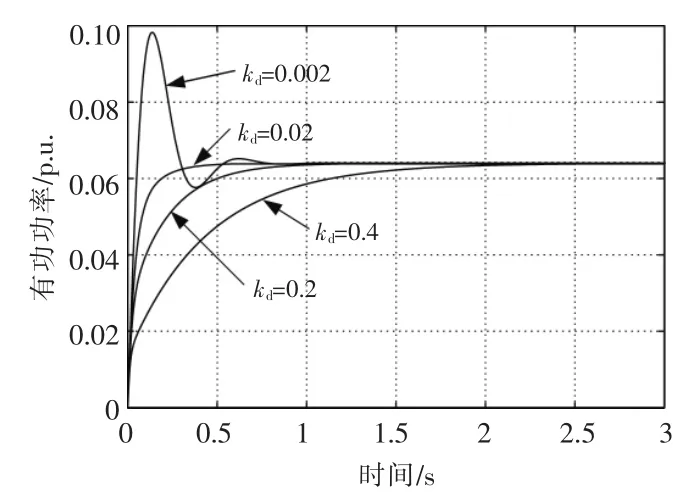
图7 不同前馈系数下改进VSG 有功环路闭环传递函数阶跃响应Fig.7 Step response of traditional close-loop transfer function of improved VSG
对比图5,7 可以看出,不同前馈阻尼系数下,当频率受到扰动情况时, 储能系统输出功率始终与整定的一次调频特性保持一致。 验证了本文所提出的一次调频与阻尼环节功率解耦的正确性。
3 改进VSG控制的稳定性分析
本文将对前馈阻尼控制下VSG 的稳定性进行分析,并与传统VSG 控制方法进行对比。 根据式(7),得出改进后VSG 的自然振荡频率及环路阻尼系数分别为
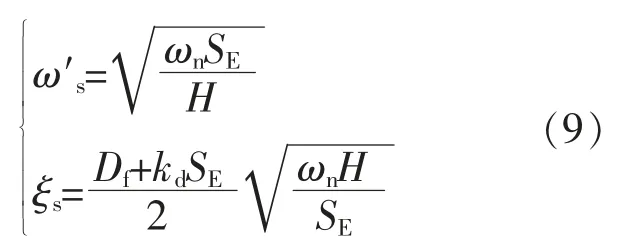
本文中改进后的VSG 的自然振荡频率未发生变化,且阻尼特性仍取决于前馈阻尼系数kd,即可通过调整前馈系数的值,使得VSG 表现出不同的阻尼特性。 图8 给出了本文所提策略中不同前馈系数时有功环路的Bode 图,图9 给出了不同虚拟惯性时间常数和前馈系数下VSG 控制的根轨迹曲线。

图8 改进后VSG 有功环路频率响应图Fig.8 Frequency response of Improved VSG control
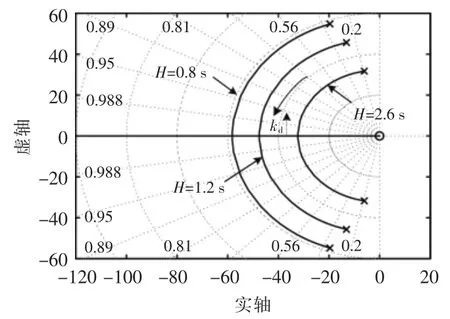
图9 改进后VSG 有功环路根轨迹曲线Fig.9 Root loci of improved VSG control
由图8 可以看出,改进后的VSG 控制在不同的前馈阻尼系数时,稳态情况下均具有单位增益,即前馈阻尼系数的引入不影响有功环路对给定功率参考的跟踪。 再结合图9 所示的根轨迹曲线可以看出, 在一定范围内, 随着前馈阻尼系数的增加,系统的阻尼特性逐渐增强。 因此,本文所提前馈阻尼策略具有与传统阻尼方法相同的表现,且不影响系统的一次频率调节,改进后的VSG 控制的具体参数可根据图8,9 进行整定。
4 仿真验证
为验证本文所提出的前馈阻尼VSG 控制策略以及参数分析的有效性, 利用Matlab/Simulink搭建了380 V/20 kW 的VSG 控制储能系统的仿真模型,其主要电路参数及控制参数见表1。

表1 VSG 控制储能变流器主要参数Table 1 Main parameters of VSG based converter
利用搭建的仿真模型对传统VSG 控制中的一次频率调节与阻尼环节的耦合特性进行验证。仿真开始时刻, 储能系统输出有功功率为0,1 s时,电网频率突变为50.05,49.95 Hz,仿真结果如图10 所示。
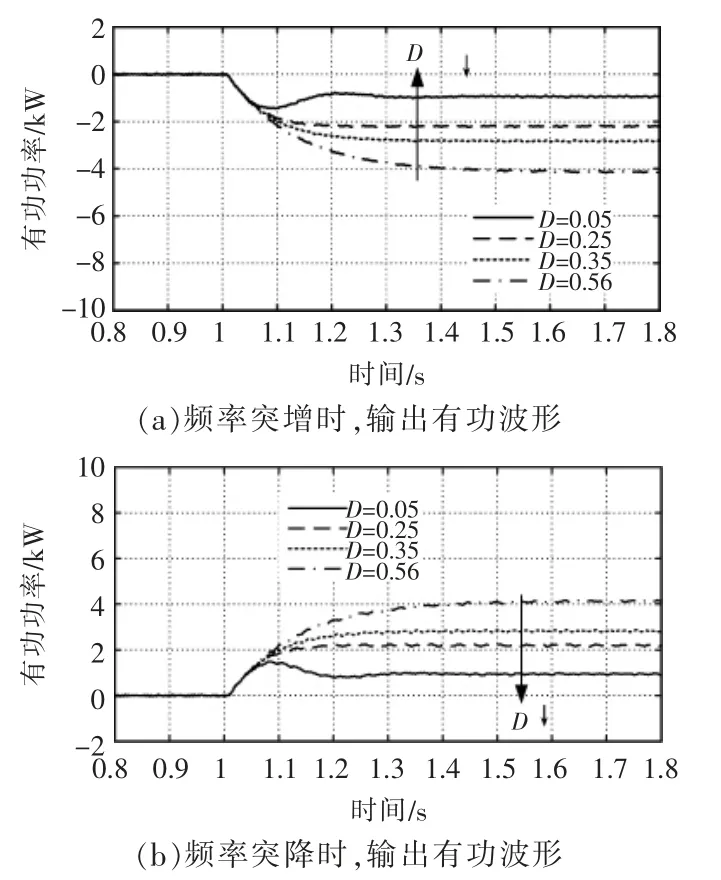
图10 电网频率波动±0.05 Hz 时,不同阻尼系数下仿真结果Fig.10 Simulation results under different D,with±0.05 Hz step
由图10 可知, 当电网频率发生变化, 传统VSG 控制中一次调频策略的有功增量受到阻尼环节严重干扰, 且阻尼系数越大, 干扰程度越严重。 本文提出了通过改变阻尼回路的反馈路径实现两者解耦的改进型VSG 控制策略。
当电网频率波动±0.1 Hz 时, 传统VSG 控制输出功率波动的仿真结果如图11 所示。
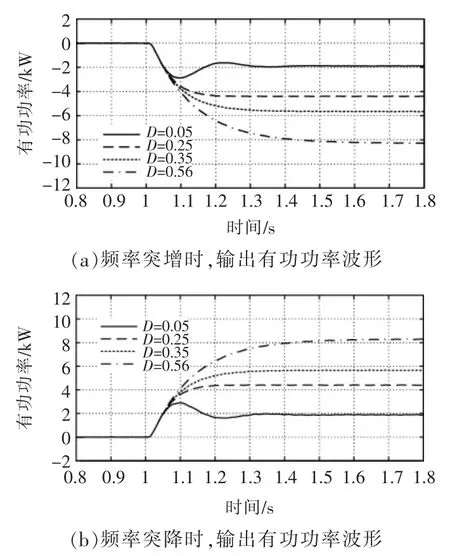
图11 不同阻尼系数下仿真结果Fig.11 Simulation results under different D
由图可以看出, 仿真结果与频率波动±0.05 Hz 时相似。 均表明传统VSG 控制下,阻尼系数对一次调频存在干扰。
根据图6 改进储能系统VSG 的有功控制环路,设定初始输出功率为0,在1 s 时刻电网频率突降0.05 Hz,仿真结果如图12 所示。
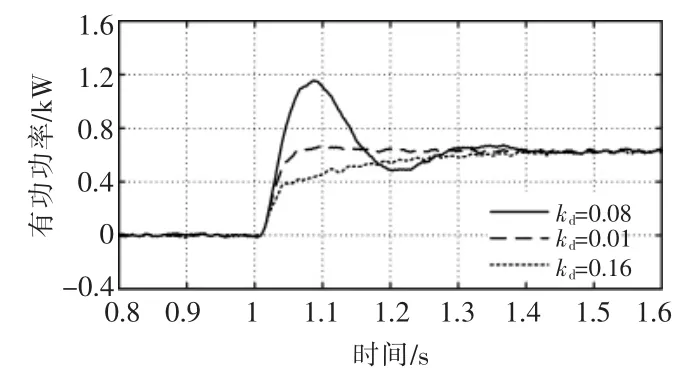
图12 前馈阻尼回路控制下仿真结果Fig.12 Simulation results under different kd
由图12 可以看出: 不同的前馈阻尼系数对VSG 暂态过程产生不同的影响,且前馈阻尼系数越大,系统超调越小,稳定性越强;电网频率突变后,稳态时储能系统输出功率保持一致,即不同的阻尼系数对一次调频功率增量不产生影响。 电网频率波动±0.1 Hz 仿真,结果如图13 所示。

图13 前馈阻尼回路控制下仿真结果Fig.13 Simulation results under different kd
由图13 可以看出,此时有功功率变化趋势与图12 所示仿真结果保持一致。对比改进前后的仿真结果可以看出, 本文所提出的虚拟阻尼前馈VSG 控制具有可行性。
在前馈虚拟阻尼kd=0.1 作用下,进行VSG 系统的满功率阶跃响应仿真,其结果如图14 所示。
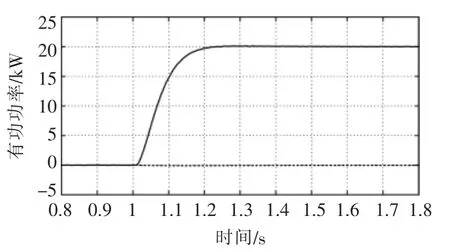
图14 改进VSG 控制下储能系统功率阶跃仿真结果Fig.14 Active power step response of ESS with the improved VSG control
由仿真结果可以看出,有功功率变化平缓,不存在超调,动态响应特性较好,证明了所提方法的有效性。
5 结论
针对传统虚拟同步发电机控制中阻尼环路与一次调频特性存在功率耦合的问题, 本文提出了一种虚拟阻尼前馈的改进型VSG 控制方法。通过建立的频率数学模型分析可知, 本文所提出的阻尼控制策略可实现储能系统准确的一次调频功率输出,且VSG 控制的阻尼特性未发生改变。最后,在Matalb/Simulink 中搭建了380 V/20 kW 的储能并网仿真模型, 通过对不同电网频率突变情况下储能系统输出功率波形的对比仿真, 验证了本文所提解耦控制策略的可行性以及参数分析的有效性。
