无梁板在极小半径弯桥中的应用及其受力分析

朱 纯 海

(江苏中设集团股份有限公司，江苏 无锡 214000)

0 引言

无梁板桥在我国已有多年的发展历史了，此种桥型大致有以下特点：1)上部结构高度小，桥下空透，可有效缩短总体桥长；2)整体性强，纵横双向受力；3)构造上机动灵活，适应性强；4)施工模板制作简单[1]。鉴于无梁板桥的上述特点，使其在平曲线半径很小，净空严格受限的条件下有其独特的适用性。

1 概述

海门市某工程在两条相互垂直且相隔一条河道的道路间需要修建一座连接桥。桥梁处于平曲线半径为25 m的弯道上，桥梁跨越的河道水面宽约37 m，河道在洪水期为泄洪通道，水位较高，要求桥下应有足够的过水断面，结构建筑高度需控制在0.7 m以内。桥位处河床以下约2.5 m厚为承载能力低的淤泥质土层。

鉴于平面极小半径的限制，预制空心板梁、T梁或工字形梁无法满足布设要求，现浇施工的箱形截面梁不满足建筑高度要求，而现浇施工的无梁板桥可有效降低上部结构梁高并便于施工；同时考虑到桥位处地质条件可适应墩梁固结时的温度效应，固结体系既可以解决支座设置的困难，又能规避弯梁桥在梯度温度等外部荷载作用下面外运动的风险，采用了三跨连续的无梁板连续刚构体系。

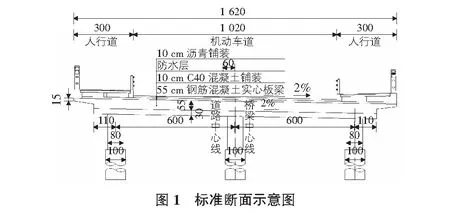
桥梁顺弯道方向跨径布置为3×13 m，桥墩径向布置。桥梁总宽16.2 m，断面组成为3 m人行道+10.2 m机动车道+3 m人行道=16.2 m。上部结构采用55 cm等厚实心板，下部结构采用柱式墩，钻孔灌注桩基础，桥墩与板梁均采用固结形式形成连续刚构体系，墩顶两侧各设置30×30 cm的倒角增加抗冲切面积。桥台根据台后填土高度分别采用桩柱式桥台与薄壁式桥台，钻孔灌注桩基础见图1。

鉴于本桥平曲线半径仅25 m，宽跨比约为1.25，空间受力性能明显，常规的平面计算已不能满足分析要求，故采用空间有限元软件来计算分析该桥的受力特性。

2 空间计算模型的建立

2.1 单元的选取

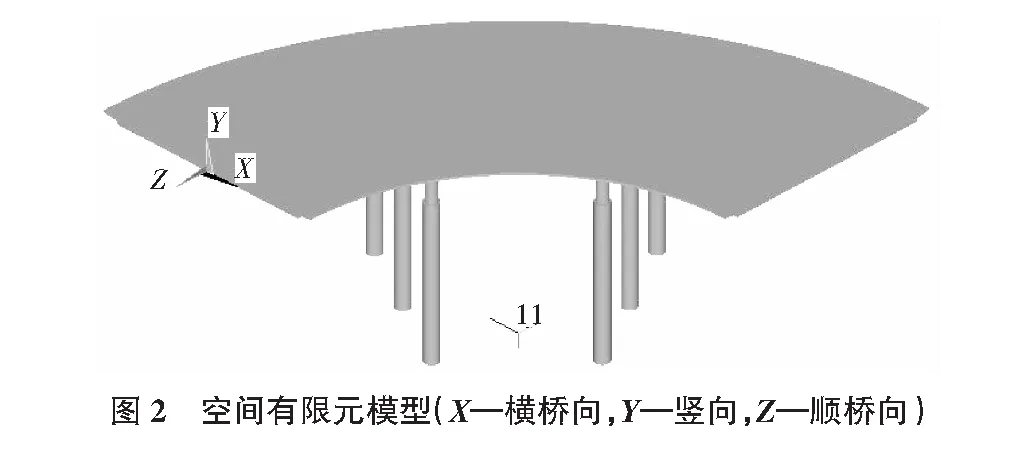
为建立能真实反映此桥受力状况的有限元计算模型，并考虑上、下部共同作用，本文采用空间实体单元模拟上部无梁板，采用空间梁单元模拟桩和柱，采用弹簧单元模拟桥台处橡胶支座和土对桩的弹性约束。

2.2 边界条件的确定

模型的边界条件严格按照实际桥梁结构的外部约束确定，且考虑支座的弹簧刚度，地基土对桩基弹簧约束刚度的确定可参照文献[2]。

2.3 荷载工况的确定

根据设计的需要，应分别计算支点、跨中、4分点等几个控制断面在恒载(一恒+二恒)、汽车活载、人群活载、收缩徐变、整体升降温、温度梯度、沉降等组合作用下的最不利状态，且对不同的控制断面应选用不同的荷载组合。本文为清晰地观察此无梁板连续刚构的空间受力特点，分别计算几种荷载单项作用效应，具体空间有限元模型如图2所示。

3 计算结果分析

3.1 无梁板变形和应力结果分析

小半径弯梁桥的受力特点告诉我们其内外弧受力差异是明显的[3]。然而小半径弯梁桥多用于城市匝道桥，其桥面宽度通常在10 m以内，底板宽度更是多在6 m以内，故在实际断面配筋设计中并没有明显体现出内外弧钢筋布置的差别，只需计入一定的偏载增大系数得到内力控制截面配筋即可。本文中的无梁板桥由于其桥面宽度相对跨度较大(16.2 m)，底板也较宽(14.2 m)，若仍均匀布置顶底板钢筋势必造成外侧局部受拉钢筋应力水平偏高，内侧局部受拉钢筋应力水平偏低的不合理受力状态，故计算分析断面内、外侧的受力差别是十分必要的。

本文主要从荷载作用下无梁板的变形和应力分布情况来说明此种差异的存在，具体取恒载工况计算，恒载作用下上部无梁板的变形如图3所示。

由上述变形图可知在恒载作用下边跨无梁板的变形较大(最大约为2.64 cm)，中跨变形相对较小，断面内、外侧变形差异明显。恒载作用下无梁板的应力分布如图4所示(单位:Pa)。

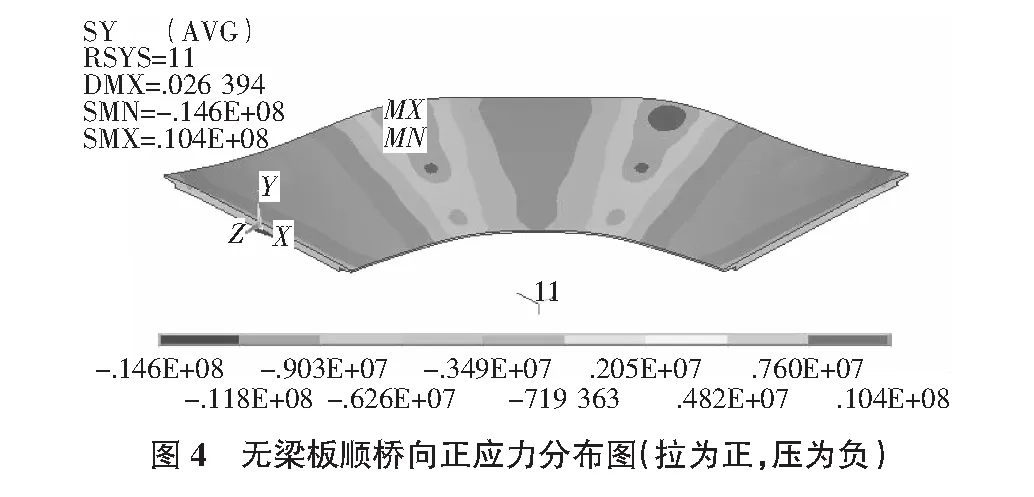
图中无梁板顺桥向正应力分布表明无论是中间固结墩支点还是跨中，横断面正应力的分布内、外侧差异明显。上述现象可近似理解如下：该桥外侧单位板宽跨径比内侧单位板宽跨径要大，故相同径向位置截面弯矩外侧自然比内侧要大。

通过上述对无梁板的断面受力不均匀性的分析，在具体设计中根据各控制断面在各自最不利荷载工况下的应力计算结果，分别取内、外侧单位宽度断面进行应力积分即可得到内、外侧单位宽度范围内的内力，进而得到纵向受力配筋，最终将这种横截面内外弧的差异性反映到设计配筋中。

除了需要沿纵向配置受力主筋外，我们还应关注无梁板的横向受力尤其是端横梁和固结墩处横向受力，图5(单位：Pa)反映了恒载作用下无梁板的横向应力。

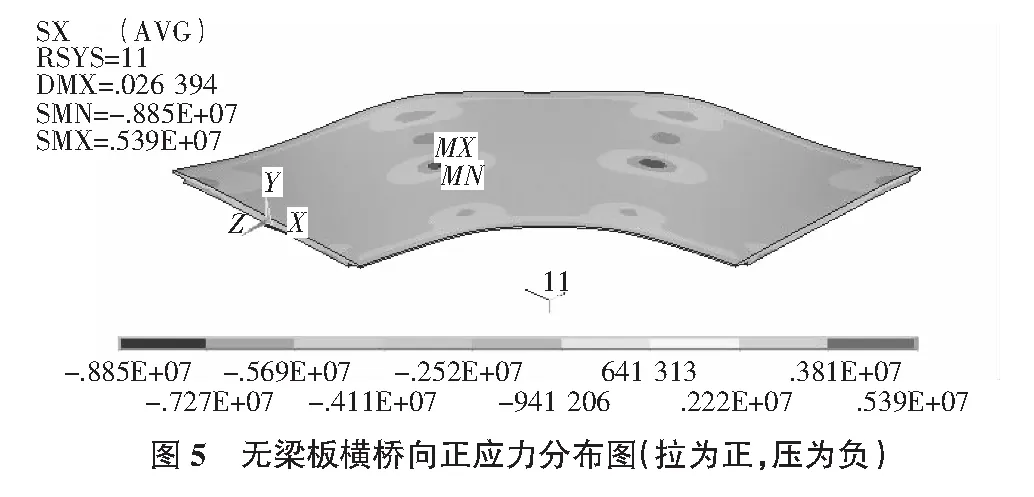
从图5可以直观看到此无梁板固结墩处明显呈现出梁体受力特性，即支点处上缘受较大拉应力(最大达可5.4 MPa)，下缘受较大压应力(最大约6 MPa)，横梁跨中处则下缘受较大拉应力，上缘受较大压应力，故在设计时应取出横梁计算其最不利工况截面内力并按暗梁方式配筋。横梁计算截面宽度建议取自墩顶两侧倒角边缘向外各延伸一半板厚，根据应力合成内力单独配筋。

3.2 无梁板刚度计算结果分析

鉴于无梁板桥的梁高与跨度比值较小，需解决三个问题：1)无梁板刚度是否能满足规范要求；2)梁体是否需设置预拱度；3)若需要设置预拱度，横向又应如何设置。

下面就这三个问题一一分析如下：

1)考虑长期效应影响活载单独作用下的刚度验算。

从图6可知活载单独作用下上部无梁板的最大竖向挠度为0.92 cm，长期挠度系数η=1.425，则考虑长期挠度后的活载挠度为1.425×0.92=1.31 cm

2)是否设置预拱度的判断。

根据荷载频遇效应组合并考虑长期效应影响可得长期挠度为4.66 cm>L/1 600=0.8 cm，故应设预拱度。

3)预拱度的设置方法。

由文献[4]可知预拱度的设置应按结构自重和1/2可变荷载频遇值计算的长期挠度值之和反向设置即可，得到最大的预拱度值为4.2 cm。而应引起注意的是该桥由于位于平面极小半径R=25 m的弯道上，故其预拱度的设置不同于一般直桥的设置方法，在同一径向横断面上沿径向不同位置处应设置不同的预拱度值，全桥预拱度的设置应是一个空间的概念。本文建议设置方式如下：先得到边跨、中跨中部内外侧最小、最大预拱度值，在同一径向横断面内预拱度从内往外按线性插值设置，边跨和中跨顺桥向的预拱度设置方式按二次抛物线变化即可。

4 结语

1)在此种净空严格受限的极小半径弯桥中，无梁板连续刚构体现出了一定的优越性：

a.上部无梁板结构有效降低了结构高度；b.无梁板的外形简洁，施工方便；c.墩梁固结的刚构体系一方面可解决支座设置的困难，另一方面可有效地规避梯度温度等外部荷载作用下的面外运动风险。

2)在此类无梁板的设计配筋中应注意内外弧纵向受力的差异，外弧纵向钢筋间距应适当加密；设计中还应注意无梁板在边、中支承位置的横向受力，上述计算结果表明在这些位置可参考箱形梁的横梁配筋，作为梁体单独计算配筋。

3)由于无梁板的结构高度相对跨度比值较小，其整体刚度较低，在恒、活载作用下的挠度较大，应设置合适的预拱度，而预拱度的设置则同样应区分小半径内外弧上的差别。