三七育苗播种压轮仿形开沟装置的设计与试验

杨文彩，徐路路，杜一帆，郎冲冲，潘吴建

（1. 云南农业大学机电工程学院，昆明 650201；2. 上海衡拓船舶设备有限公司，上海 200031）

0 引 言

三七是驰名中外的名贵药材，是中国国家地理标志产品。由于三七的特殊生长条件，全国种植面积和产量的98%均来自于云南。目前云南省三七种植面积达到66 666 hm2以上[1]。三七育苗播种行距、株距很小，均为50 mm，播种深度仅为10 mm，属于超精密播种[2]。但三七播种农艺极其特殊，目前还没有适宜的三七育苗播种机问世，传统的人工种植模式占主导地位。使得播种季节用工成本居高不下，且播种质量不均匀。开沟装置是播种机的重要工作部件，其开沟质量的好坏直接影响种子播种后的粒距均匀性与播深一致性，进而影响种子的发芽生长[3-5]。

目前国内外对开沟装置的研究方法主要有仿形技术、仿生技术、多功能组合法等。仿形技术方面：研究了后置仿形轮、液压高程仿形、弹簧压缩水平仿形板和双向仿形平行四杆机构等，从多方面设计以控制开沟深度一致的平稳性[6-8]，Jia 等[9]设计了仿形弹性镇压辊以改善苗床特性和出苗一致性；仿生技术方面：设计了仿蚯蚓运动、野兔前爪、穿山甲鳞片、及蝗虫口器、蝼蛄前足和褐飞虱表皮的开沟器，以改善土壤耕种层结构、减粘降阻，提高破茬防堵性能[10-14]；多功能组合方面：研究了组合式同沟分层施肥播种开沟器、犁旋组合式油菜播种开沟起垄装置和多功能集成式播种开沟器，以解决土壤壅堵、土壤扰动、种床土壤紧实度不足、保证沟型垄体稳定和开沟深度均匀性问题[15-18]，Vamerali 等[19]设计了一种宽扫开沟器，实现了较高的作物残茬掺入量和开沟均匀的播种深度；以上设计的开沟器存在仿形滞后、结构相对复杂或一体化协调性不佳的问题，且针对不同作物的土壤类型也不尽相同。已有的开沟器主要是面向大豆、玉米、马铃薯等大行株距大田作物，开沟深度较深、沟距较宽，且面向的土壤紧实度相对较高，不适于行株距小、播深浅的三七育苗播种。

基于三七育苗农艺要求，急需研发开沟时对土壤扰动小和种沟底部适当紧实的密集型开沟装置，本文采用仿形技术和多功能组合法，将仿形功能、开沟功能与沟底紧实功能集中于压轮，设计三七育苗播种的压轮仿形开沟装置，并通过理论分析和试验优化方法，探索适合三七育苗播种的最佳工作参数，为后期三七育苗播种研究提供参考。

1 压轮仿形开沟装置整体结构和工作原理

1.1 整体结构

压轮仿形开沟装置整体结构主要由机架、电机、地轮、安装轴、压轮连接板、压轮和弹簧等组成，结构示意图如图1 所示。整机主要参数如表1。

图1 压轮仿形开沟装置整体结构示意图 Fig.1 Structural diagram of the overall pressing wheel profiling ditching device

表1 压轮仿形开沟装置整机主要参数 Table 1 Main parameters of the pressing wheel profiling ditching device

1.2 工作原理

压轮仿形开沟装置通过安装轴与播种机相连，播种机为自走式，由电机提供动力。作业时，压轮随着播种机前进，一边向前滚动一边在自重和压轮连接板重力作用下压出种沟，即沿着压轮侧面向两侧运动的土壤与相邻压轮同样作用下的土壤形成倒V 型土堆，开出平底V型的种沟。未开沟时，弹簧处于拉伸状态。开沟过程中弹簧的拉伸状态不会改变，只改变拉伸程度。在相同的土壤条件下，所需开沟深度可通过安装轴和仿形弹簧拉力调节螺栓在开播前进行调试。

播种前育苗槽内的土壤可能会存在纵向波浪式不平整或横向高低不平的现象，为保证压轮压出的种沟沟深一致，将压轮按分段进行组合，进而使种子播深一致。当压轮在前进方向上遇到土壤波浪式凸起或凹陷时，压轮与地面间的接触压力增大或降低，弹簧拉伸量变化使压轮上移或下移，实现纵向仿形；在前进方向的垂直方向土壤表面不平整时，各段压轮随土壤凸起或凹陷，通过上移或下移实现横向仿形。

2 压轮仿形开沟装置关键部件设计

2.1 压轮顶宽和斜边倾角设计

前期试验发现，土壤紧实度不足易导致开沟后土壤回落量大，因而，将压轮设计成平底V 型，压轮结构示意图如图2a、2b 所示。压轮的斜边倾角结合红壤土的休止角进行设计，红壤土休止角经测定仪进行5 次测定取平均值，即得到红壤土休止角为40～50°；压轮顶部宽度考虑三七种子的三轴尺寸和土壤回落量进行设计，压轮顶宽ζ 及斜边倾角α 如图2c 所示；其他尺寸依据文献[20]选取：压轮直径150 mm，压轮厚度为20 mm，两相邻压轮间距为30 mm 保障土壤流通性。

图2 压轮结构示意图 Fig.2 Structural diagram of pressing wheel

2.1.1 压轮顶宽设计

压轮顶宽尺寸要能保证土壤回落后三七种子也能完全落入种沟底部，而三七种子三轴尺寸的平均值主要集中在5.0～6.3 mm 之间，最大值为7.2 mm[21]，故设计平底V 型压轮的顶宽为8 mm。

2.1.2 压轮斜边倾角设计

适适宜三七育苗播种的红壤土或棕红壤土，土质疏松、通透性好[22]，将土壤视为散粒体并假定开沟过程中压轮做匀速运动，耕深稳定[23]。结合红壤土的休止角，对压轮斜边的分析如图3a 所示，ZZ2和I2I 为压轮的斜边，Z2I2为压轮的顶宽。开沟时土壤被挤压到两轮之间，压轮压出种沟离开后会有少量土壤滑落种沟底部，最终形成稳定的垄峰I2H E2交汇于H 点。沟底的理论宽度等于压轮顶宽Z2I2，I′E′为相邻两压轮间的土壤在土壤表面的投影距离，也是压轮间的理论间距，I2I′为压轮V 形斜面在土壤表面的投影距离，其长度由压轮的厚度ZI（20 mm）和顶宽Z2I2（8 mm）共同决定，通过计算可知I′H′为垄峰中心线HH′到压轮侧面I I′的距离，其长度由压轮间距I′E′决定，且I′E′关于HH′对称，可知I′H′ = I′E′/2 = 15 mm。设垄峰高度HH′为l，则l 可按下式计算

图3 相邻压轮触土间距分析与滑坡稳定性验证 Fig.3 Analysis of contact position of adjacent pressing wheel and verification of landslide stability

根据红壤土的休止角α 为40°～50°，可计算得垄峰高度h 为17.62～25.03 mm，故而压轮斜边倾角设计满足三七育苗播种时开沟深度为20 mm 的要求。

压轮斜边倾角α 为45°时，垄峰高DH 为21 mm，考虑土壤回落情况，现对垄峰斜坡进行滑坡稳定安全系数验证，用微元法取垄峰斜坡土壤对其进行受力分析，如图3b。土壤的抗滑力根据直线破裂面法假定土壤颗粒的下滑为土壤体沿着临界坡面自然下滑，滑坡稳定安全系数K 的计算如下[25-26]

式中M 为滑体自重力，kN/m；τ 为土壤抗滑力，kN/m；σ 为土壤的正应力，kPa；α0为滑面倾角，（°）；φ 为滑动面上土体的内摩擦角，（°）；c 为滑动面上土壤的黏聚力，kPa；T 为土壤滑动力，kN/m；K 为滑坡稳定安全系数；β 为滑坡倾角，（°）；J、J1、J2为滑体的三个顶点；|JJ1|为J、J1两点间滑面的长度，m；

根据式（2），砂质壤土滑坡稳定安全系数可取为

因为c·|JJ1|/(M·sinβ)＞0 恒成立，当φ＞β 时，K＞1，此时抗滑力τ 大于滑动力T，满足滑坡稳定条件，压轮斜边倾角设计合理。

2.2 压轮连接板设计

2.2.1 结构设计

压轮连接板包括压轮中间连接板和压轮侧连接板，根据杠杆原理，结合整体机架宽度和开沟行距进行压轮连接板结构设计，每块连接板上安装两个压轮，每组压轮用一块加强筋加固，分多组设计便于实现横向仿形，其中一组结构示意图如图4 所示。压轮中间连接板上端U的圆孔用于连接弹簧，V 端圆形孔与压轮连接头配合，连接头再与压轮进行配合；安装轴套筒2 套在安装轴上并以安装轴为杠杆支点（与安装轴套筒同轴心的位置）进行固定和高度调节。

2.2.2 主要参数确定

压轮连接板的尺寸由安装轴离地面的高度、开沟深度、弹簧预拉力、杠杆支点位置及V 端压轮连接板质量与压轮质量之和共同决定，当压轮中间连接板A1B1与土壤表面的夹角θ（见图5）最大时，依据弹簧预拉力最小和安装轴安装位置最低时的空间，确定弹簧连接孔与V端圆形孔之间的总长度A1B1为270 mm，为确定杠杆支点O 的位置，设A1O 为x1、B1O 为x2，则x1+x2=270 mm，x1、x2的取值通过压轮中间连接板的受力分析进行计算，压轮中间连接板受力简图如图5, 考虑压轮开沟深度浅，与土壤接触面积小且接近压轮最底端，故将FQ简化为垂直方向的力。

在临界条件下，假设土壤为非刚性表面承受载荷，由土壤下陷量公式[27]计算得压轮受到的载荷FQ

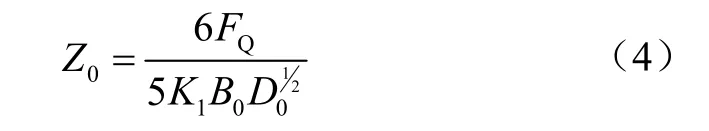
式中Z0为压轮的下陷量（即开沟深度），mm；FQ为压轮作用于地面的压力，N；B0为压轮的宽度，mm；D0为压轮的直径，mm；

K1为土壤特性系数；α1为与土壤性质有关的参数，由农业机械学[28]取α1=1.4。开沟深度取临界值20 mm，由式（4）、（5）可得单个压轮受到的载荷FQ=27.83 N。

根据图5，受力平衡时有

FT用拉力计通过试验最优法测量，由式（6）、（7）可计算得x1为165 mm，x2为105 mm，即最终确定杠杆支点O 的位置。

2.2.3 变形量分析

压轮连接板结构尺寸将决定其是否发生扭转变形、焊接处断裂等情况，进而影响播种。因此借助ANSYS 软件进行压轮连接板的应力、应变和变形分析。材料定义为Q235 钢材；网格划分选用自动划分法（Automatic），共划分为8 634 个单元，16 337 个节点；施加的载荷按开沟深度为20 mm 时，单个压轮所受载荷FQ为27.83 N；根据该装置设计的实际情况，约束条件选择固定约束并设定在安装轴套筒两端；最后进行求解，压轮连接板的应力、应变和变形量云图如图6所示。

图6 压轮连接板的应力、应变和变形云图 Fig.6 Stress, strain and deformation contours of pressing wheel connecting plate

由图6a、6b 可知，应力、应变最大处均位于压轮中间连接板与安装轴套筒连接处的上侧面以及下侧面，应力、应变最大处到安装轴套筒的受力及变形过渡性较好且没有发生突变，说明压轮连接板结构设计合理；由图 6c 可知，最大变形量位于压轮中间连接板的U 端顶部，这与弹簧拉力最大处相对应。从结构表面看，压轮连接板不存在扭转变形，说明对称式压轮连接板设计结构合理，压轮中间连接板在弹簧拉力的作用下，具有较大的变形量，但由于加强筋的作用使各连接板受力变形相对较小。

通过以上分析可知：压轮连接板应力最大处应变也最大，但在加强筋的作用下最大应力应变处的变形量显著降低；在压轮中间连接板的U 端变形量较大，说明此结构能有效降低扭转变形和断裂的可能性，对U 端最大变形量处可再增添小型加强筋与现有加强筋垂直固接在U 端上表面，进行加固。

2.3 弹簧选型

压轮工作时，土壤表面存在凹凸不平的变化，使压轮作用于连接板的力与弹簧的拉力都发生相应的变化，如图7所示，当压轮中间连接板A1B1绕O 点转动到C1D1位置时，压轮中间连接板A1B1与土壤表面E1F1的夹角∠B1A1F1也发生变化，通过测量得∠B1A1F1=30°转变为∠D1C1F1´=9.59°，此时对应压轮的仿形量即压轮中间连接板绕O 点转动时压轮摆动的垂直高度C1E1为55 mm，而开沟深度增加了5 mm，故利用开沟深度不同时与压轮的仿形量对应的弹簧变化量求得弹簧刚度，进而选取弹簧的型号。

因压轮的仿形量不同时弹簧的拉伸变形量也不同，根据图 7 由压轮中间连接板变化的几何关系得：A1C1=C1E1/sin∠C1A1E1=60.79 mm，由E1F1平行于C1F1′、∠B1A1F1=30°、∠D1C1F1′=9.59°，求得∠C1OA1=20.41°、∠OA1C1=85.21°、∠C1A1E1=64.79°；由三角形比例关系B1D1/A1C1=D1O/OC1，得拉力弹簧变化量 B1D1为38.69 mm。

图7 仿形量示意图 Fig.7 Diagram of profiling amount

当压轮中间连接板由A1B1转动到C1D1位置时，A1B1与土壤表面的夹角由30°转变为9.59°，此时开沟深度将从15 mm 加深到20 mm，根据式（4）和（5），土壤作用于每个压轮的支撑力分别为：FQ1=20.87 N、FQ2=27.83 N，此时压轮处于平衡状态。压轮受力情况如图8 所示，FQ1、FQ2简化为垂直方向的力。

图8 压轮受力分析 Fig.8 Force analysis of the pressing wheel

以任一组压轮仿形开沟装置为例，根据开沟深度稳定性和力矩原理列出平衡方程：开沟深度为15 mm 时

开沟深度为20 mm 时

计算得：开沟深度为15 mm 时，弹簧拉力大小为FT1=107.86 N；开沟深度为20 mm 时，弹簧拉力大小为FT2=187.52 N。

拉力弹簧变化量Δx 为38.69 mm，弹簧拉力变化量为ΔF=FT2-FT1=79.66 N。根据胡克定律F=k·x，则有

求得弹簧刚度k=2.06 N/mm。

当开沟深度为 15 mm 时，弹簧的伸长量L1=FT1/k=52.36 mm，当开沟深度为20 mm 时相对于开沟深度15 mm 时的变化量Δx 为38.69 mm，所以拉力弹簧伸长量的最大值L=L1+Δx =91.05 mm 时，根据弹簧刚度值，按照《GB2088—2009 普通圆柱螺旋拉伸弹簧及其参数》选取LI A 4.0×45×12.25 GB/T2088 型号的拉力弹簧，相关参数如表2 所示。

表2 拉力弹簧参数 Table 2 Tension spring parameters

3 开沟试验

为验证本文设计的三七育苗播种压轮仿形开沟装置，试制样机后进行二次正交旋转组合试验，田间试验开沟过程如图9 所示。

图9 田间开沟试验 Fig.9 Field ditching test

3.1 试验条件

2018年12月在云南农业大学大河桥三七育苗基地进行育苗播种试验。育苗槽参数：长度80 m，宽度1.5 m，土层深度30～35 cm，土壤湿度在20%～30%。测量工具：数显游标卡尺（精度0.01 mm）、湿度测量仪、ARN-JSDY土壤紧实度仪、休止角测定仪、量角器、钢板尺等。

3.2 评价标准及测量方法

开沟质量用开沟深度稳定性来评价，测量方法根据NY/T740—2003《田间开沟机械作业质量》执行。开沟深度平均值和开沟深度稳定性分别为

式中Ha为开沟深度平均值，mm；hi为第i 个测量点的深度值，mm；N0为在作业区选择的测量点数，N0=10。

式中S 为开沟深度标准差，mm；W 为开沟深度变异系数，%；Q 为开沟深度稳定性系数，%。

3.3 二次正交旋转试验与结果分析

3.3.1 试验设计

根据对仿形结构、开沟结构与压实结构的分析和相关学者的研究[29-31]，选取土壤紧实度、播种机前进速度和弹簧预拉力为试验因素，各因素水平的取值范围在课题组单因素试验的基础上分别选取在100～300 kPa、6～8 m/min 和180～220 N，以开沟深度稳定性为试验指标，按照三因素二次正交旋转组合试验设计方法，试验因素水平编码如表3 所示。

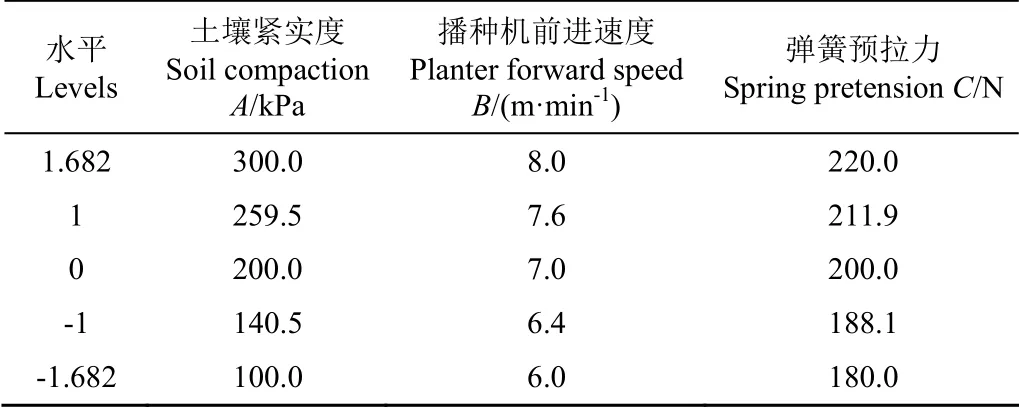
表3 试验因素水平编码 Table3 Test factor and level

3.3.2 试验方案与结果

进行23 组试验，每组试验重复3 次取平均值，试验方案与结果如表4 所示。

3.3.3 回归方程与显著性检验

运用Design-Expert 10.0.3 软件对试验数据进行回归分析[22,26,32]，得到开沟深度稳定性Y1的方差分析表5 和回归方程。

根据表5 可知，开沟深度稳定性Y1的回归模型达到极显著（P＜0.01），说明该回归模型与自变量具有显著的函数关系；对于失拟项不显著（P＞0.1），说明模型是合适的，开沟深度稳定性回归模型拟合度较高。在开沟深度稳定性回归方程中A 对开沟深度稳定性影响显著（P＜0.05），B 对开沟深度稳定性影响极显著（P＜0.01），AC 交互作用极显著（P＜0.01），A2极显著（P＜0.01）和C2显著（P＜0.05），其他因素影响不显著。通过F 检验，得出影响开沟深度稳定性的主次顺序为播种机前进速度、土壤紧实度、弹簧预拉力，与显著性检验结果吻合。

表4 试验方案与结果 Table 4 Test design and results

表5 开沟深度稳定性的方差分析 Table 5 Variance analysis of ditching depth stability

将表5 中不显著因素剔除后，得到试验因素与试验指标的回归方程如下

式中A 为土壤紧实度，kPa；B 为播种机前进速度，m/min；C 为弹簧预拉力，N；

由方差分析可知AB、BC 对开沟深度稳定性的交互作用并不显著，但在田间试验时发现AB、BC 对开沟深度稳定性的交互作用存在影响，为确定这种影响关系的影响程度，将进行AB、BC 对开沟深度稳定性的交互作用响应曲面的分析。

3.3.4 各因素对试验指标的影响效应分析

应用Design-Expert10.0.3 软件分析得到土壤紧实度、播种机前进速度、弹簧预拉力3 个因素中任意两个因素分别对开沟深度稳定性的交互影响，响应曲面如图 10 所示。

图10 各因素对开沟深度稳定性的响应曲面 Fig.10 Response surface of various factors to ditching depth stability

由图10a 可知，当弹簧预拉力为210 N 时，若土壤紧实度固定，开沟深度稳定性随着播种机前进速度增加而基本缓慢降低，播种机前进速度最优范围在 6.21～7.5 m/min；若播种机前进速度固定，开沟深度稳定性随着土壤紧实度增加而降低，土壤紧实度最优范围在100～270 kPa。

由图10b 可知，当播种机前进速度为6.41 m/min 时，当土壤紧实度固定在100～186.93 kPa，弹簧预拉力固定在180～197.83 N 内，开沟深度稳定性随着土壤紧实度和弹簧预拉力的增加而增加，但开沟深度稳定性低于85%；当土壤紧实度固定在186.93～266.12 kPa 内，弹簧预拉力固定在197.83～212.11 N 内，开沟深度稳定性随着土壤紧实度和弹簧预拉力的增加先快速增加，后略有缓慢降低，但开沟深度稳定性最低值大于85%；当土壤紧实度固定在266.12～300 kPa，弹簧预拉力固定在212.11～220 N 内，开沟深度稳定性随着土壤紧实度和弹簧预拉力的增加而降低，开沟深度稳定性低于85%。

由图10c 可知，当土壤紧实度为252.40 kPa 时，若播种机前进速度固定，开沟深度稳定性随着弹簧预拉力增加而缓慢降低，弹簧预拉力最优范围在180～216 N；若弹簧预拉力固定，开沟深度稳定性随着播种机前进速度增加而缓慢的降低，播种机前进速度最优范围在6～7.5 m/min。

由试验因素对开沟深度稳定性的交互影响分析，确定了土壤紧实度、播种机前进速度和弹簧预拉力交互试验因素下的最佳工作范围，为参数优化提供试验因素优化范围。

3.3.5 参数优化

为获得开沟深度稳定性最佳的开沟参数，以土壤紧实度、播种机前进速度和弹簧预拉力为自变量，以开沟深度稳定性最佳为目标，结合3.3.3 节中得到的回归方程，建立如下优化数学模型

借助Design-Expert 10.0.3软件的Optimization模块对其进行求解，得到开沟深度稳定性最佳的各变量取值为：土壤紧实度259.50 kPa，播种机前进速度6.40 m/min，弹簧预拉力211.90 N，此时开沟深度稳定性为89.41%。

采用上述最优参数组合开展土槽试验，对开沟深度稳定性进行试验验证。为消除随机误差进行4 次试验取平均值。由土槽试验得到开沟深度稳定性平均值为86.43%，与模型优化求解的结果89.41%误差为2.98%，验证了优化后最佳参数组合的可信性，试验效果如图11 所示。

图11 优化后开沟深度 Fig.11 Diagram of optimized ditching depth

4 结 论

结合三七行株距小、播深浅且对播种深度一致性要求高的特殊播种农艺，设计了一种三七育苗播种压轮仿形开沟装置。该装置可实现横纵向仿形开沟、同时可对疏松土壤进行适当压实。

通过三因素二次正交旋转组合试验方法进行试验，并对试验结果进行方差分析，得出影响开沟深度稳定性的因素依次为播种机前进速度、土壤紧实度、弹簧预拉力。建立开沟深度稳定性优化模型，运用Optimization 模块对其进行求解，得到压轮仿形开沟装置各试验因素的最优组合为：土壤紧实度为259.50 kPa，播种机前进速度为6.40 m/min，弹簧预拉力为211.90 N，此时开沟深度稳定性为89.41%；土槽试验验证得到开沟深度稳定性为86.43%，与软件优化值基本吻合。从最终开沟效果来看，本文设计的压轮仿形开沟装置开沟效果较好，满足三七开沟的作业质量要求。