新课标下高中函数值域、最值求解方法的探究
2020-05-19杨煜东内蒙古自治区呼和浩特市第二中学
杨煜东 (内蒙古自治区呼和浩特市第二中学)
函数值域问题和最值问题是两个不同的概念。简单地说,存在最值的函数,其未必有确定的值域;反之,值域确定的函数未必有最大值、最小值。只是在常见的一些函数中,函数值域与最值的求解方法是相通的、类似的。归纳起来,常用的方法有:观察法、配方法、分离常数法、判别式法、反解法、数形结合法、换元法、均值定理法、对勾函数法、导数法
一、观察法
某些函数形式比较简单,可以通过观察法较为迅速地得出函数值域,例如求下列函数的值域:
(2)f(x)=1-2x,x∈R
分析:以上三个函数分别属于含绝对值函数、一次函数、分段函数,其定义域已经给定,其各自的值域我们可以通过观察的方法迅速得到,分别为:(1){-1,0,1};(2)R;(3){0,1}
二、配方法
以二次函数的相关性质、图像为依托,利用数形结合思想求解某函数在给定区间的最值和值域问题。这种方法一般适用于形如:
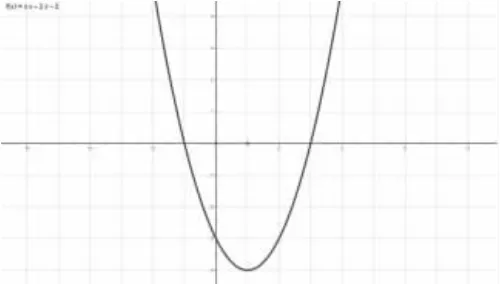
求函数的值域:f(x)=x2-2x-3,x∈[-2, ]2
分析:f(x)=(x-1)2-4
此函数为标准一元二次函数,其图像为
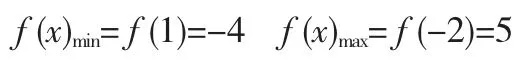
小结:对二次函数型值域问题,我们通常可以采用配方并结合图像的方法求解。
三、分离常数法
分析:由x2+x+1>0 得,该函数定义域为R

令 u=x2+x+1,则
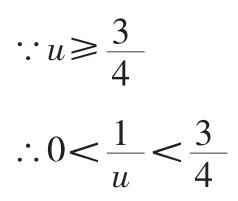
小结:分离常数的方法也可用于上述类型函数值域的求解,同时,以上解法中整式相除的方法值得关注,会为我们解题带来便利。
当然上述例题也可以用其他方法求解.
四、判别式法
(1)在△≥0中,应考虑“=”是否成立
(2)由于在变形过程中涉及去分母,故应考虑函数的定义域是否为R
(3)应讨论 f(y)=0 的情形
(4)原函数定义域应为自然定义域
分析:原函数变形为(x2+x+1)y=3x2+3x+1整理得(y-3)x2+(y-3)x+y-1=0,(*)
(1)y-3=0 时,方程式不成立
(2)y-3≠0 时,(*)式在 x∈R 时有解,
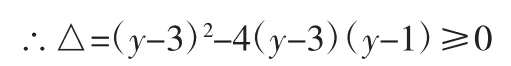
小结:该解法将函数值域问题转化为判断方程根的问题,利用一元二次方程的判别式求解值域。
注:本解法更适用于定义域为R 的两个二次式相除的值域问题。
五、反解法
分析:原函数变形得2y+ycosx=2-sinx
即sinx+ycosx=2-2y
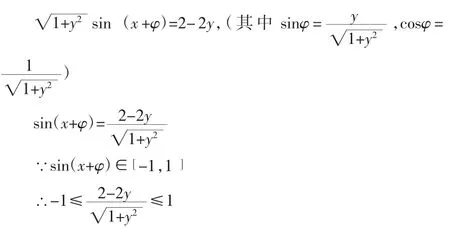
小结:这种方法是利用某些函数的特性,例如有界性,将原函数反解,转化为关于函数值y 的不等式,进而求解出原函数的值域。
一题多解是数学中培养学生思维能力的很有效的一种方法,像上述这道题我们还可以借助于数形结合的思想探究该问题。
六、数形结合法
数形结合是高中数学核心素养中要求学生掌握的一种重要的思维方法。形是数的外在表象,数是形的灵魂实质,华罗庚先生曾讲:数缺形时少直觉,形少数时难入微,数形结合百般好,隔离分家万事休。足见数形结合思想的重要性。
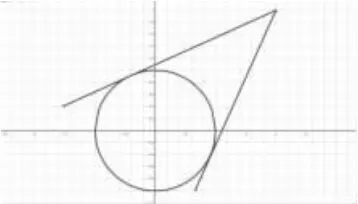
我们可以给上式赋予一定的几何含义——斜率k
可以理解为点 P(-cosx,sinx)和点 Q(2,2)连线的斜率,而P 点是单位圆上的点,结合上图
由图可知:PQ 连线介于图中两条切线之间,我们可以建立PQ 的直线方程为:
y-2=k(x-2),即 kx-y+2-2k=0
数形结合思想将“数”与“形”有机地结合在一起,使得我们的抽象思维具有现实的依托,更便于我们对知识的理解与探究。
七、换元法
很多时候,试题中的已知和待求的结论很难看出直接联系,甚至是相去甚远。因此,为了建立已知和未知的联系,我们常常会引进一个(或几个)新的变量来替代原有的变量,旨在揭示出已知与未知之间被表面形式掩盖着的实质,从而探究出解题的切入点。换元法是一种重要的解题方法,掌握这种方法的关键是构造变换式,常见的换元形式有:代数换元、三角换元、参数换元。
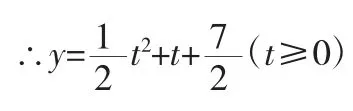
小结:处理上述类型无理函数常用的方法是将其转化为有理函数,通过换元的方法,将原函数转化为t 的二次函数问题。
八、基本不等式法(均值定理)
均值定理的核心:如果若干个正数的积(或和)为常数,则当且仅当这若干个正数相等时,它们的和(或积)有最小(或最大)值。
求下列函数的值域
分析:
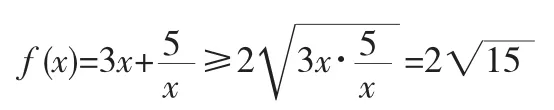
分析:
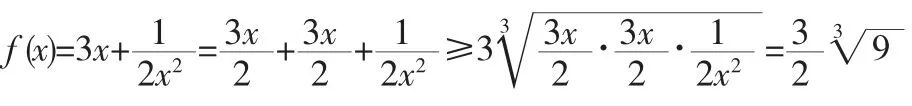
小结:针对某些函数,我们可以通过变形,构造均值定理的基本形式,利用均值定理求解函数值域,但应注意均值定理适用的条件——“正,定,等”,如果我们遇到“貌合神离”的试题又应如何处理呢?比如下面这个例题
九、对勾函数法
求下列函数的值域
分析:
若该函数用均值定理求解值域,不满足等号成立的条件,于是上法不可取。
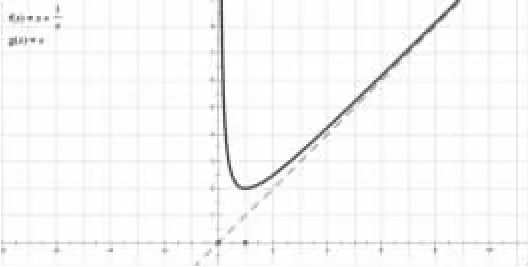
该函数图像如图
结合图像可知:f(x)在[2,+∞)上单调递增
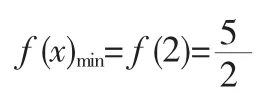
分析:
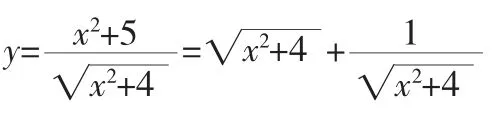
由对勾函数可得
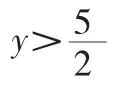
课程改革之后,将微分学的初步知识引入到了高中教材之中,为我们求解函数值域问题带来了很大的方便,使得利用导数知识研究函数问题成为一种常用的方法。
十、导数法
求下列函数的最大值和最小值
利用导数研究函数单调性,再根据定义来确定函数的值域与最值
(1) f(x)=x3-2x2+1,x∈[-1,]2的最大值和最小值
分析:
f'(x)=3x2-4x,令 f'(x)=0,得
得列表
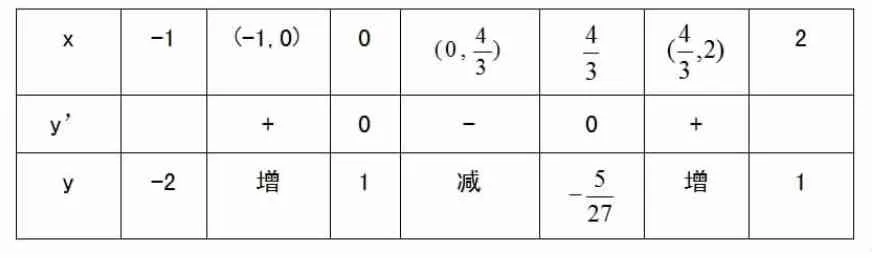
?
由表可得f(x)max=1,
所以,x∈[-1,2]时,f(x)=x3-2x2+1 的最大值为1,最小值为-2
分析:
f'(x)=3x2-3ax=3x(x-a),令f'(x)=0,得x=0或x=a
分析:
∴f(x)在区间[0,a]上单调递减,在[-1,0]和[a,1]上单调递增
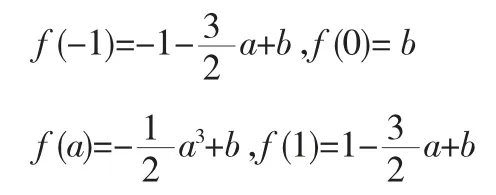
由f(x)的单调性可知,f(x)最大值只可能在f(0)和f(1)中选取f(x)最小值只可能在f(-1)和f(a)中选取
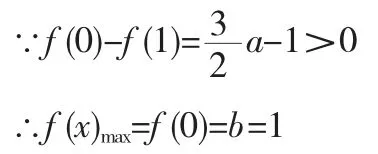
分析:
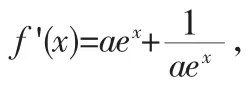
当 f'(x)>0,即x>-ln a 时,f(x)在(-lna,+∞)上单调递增;
当 f'(x)<0,即x<-lna 时,f(x)在(-∞,-lna)上单调递减;
i)当 0 <a <1 时,-Ina>0,f(x)在(0,-lna)上递减,
在(-Ina,+∞)上递增,
∴f(x)在[0,+∞)内的最小值为 f(-1ma)=2+b
ii)当 a≥1 时,-Ina≤0,f(x)在[0,+∞)上递增,
以上给出的是求函数值域的常用方法,有时还要把这些方法结合起来使用,同时在求解函数值域时也应特别关注函数的定义域、奇偶性、周期性、对称性等一系列性质,这将对我们解答试题以及探究函数问题提供很大的帮助。
