基于传热学的炉温曲线研究

摘  要：文章针对设计回流焊炉焊接系统各温区对应下的最优温度和传送带过炉速度，使用牛顿冷却定律与傅里叶定律，构建了沿传送带方向试件经过各温区温度的差分模型;进一步设计一种搜索算法，在允许的范围内，寻求出试件最大传送带过炉速度;最终设立合理的指标，使用蒙特卡洛法和模拟退火算法全局寻优，得到了各温区对应下的最优温度和传送带过炉速度。

关键词：回焊炉;炉温曲线;传热学;差分方程;搜索算法;模拟退火算法

中图分类号：TP273;TN405      文献标识码：A 文章编号：2096-4706（2020）20-0018-05

Furnace Temperature Curve Research Based on Heat Transfer

FANG Haohang

（School of Mechanical Engineering Yangtze University，Jingzhou  434023，China）

Abstract：In order to design the optimal temperature and the conveyor belt passing speed in each temperature area of the reflow furnace welding system，Newtons law of cooling and Fouriers law were used to construct the difference model of the temperature of specimens passing through each temperature area along the conveyor belt direction. A search algorithm is further designed to find the maximum conveyor belt passing speed within the allowable range. In the end，a reasonable index was set up，Monte Carlo method and simulated annealing algorithm were used to search for global optimization，and the optimal temperature and conveyor belt passing speed under each temperature region were obtained.

Keywords：reflow furnace;furnace temperature curve;heat transfer;difference equation;search algorithm;simulated annealing algorithm

0  引  言

回流焊是目前应用于集成电路板最广的焊接工艺，本文对2020年全国大学生数学建模竞赛题进一步研究，为提高回流焊接工艺的效益，提出一种设计回焊炉内各温区最佳温度的方法。通過测量的电路板在炉内任一位置温度（炉温曲线），调整模型中各参数。提出一种搜索算法，寻求出电路板最大过炉速度。由于焊接过程需要满足一定的要求，建立了合理的评估指标，最终使用蒙特卡洛法与模拟退火算法进行全局寻优，寻求出回焊炉各个温区的最佳温度以及电路板的最佳过炉速度。作者基于参加2020全国大学生数学建模竞赛的经验，对回焊炉有一定了解，希望通过建模的方法探寻最佳炉温系统，在整个过程中主要负责数学模型的推导与构建以及代码的实现。

1  回焊炉介绍

1.1  回焊炉组成

回焊炉分成4个大温区：预热区、恒温区、回流区、冷却区，如图1所示。本文中根据赛题中已知的回焊炉尺寸以及一次回流焊数据进行模型的构建，其中含有11个小温区及炉前区域和炉后区域，小温区长度为30.5 cm，间隙5 cm，炉前、炉后区域长25 cm。

1.2  回焊炉内环境与生产要求

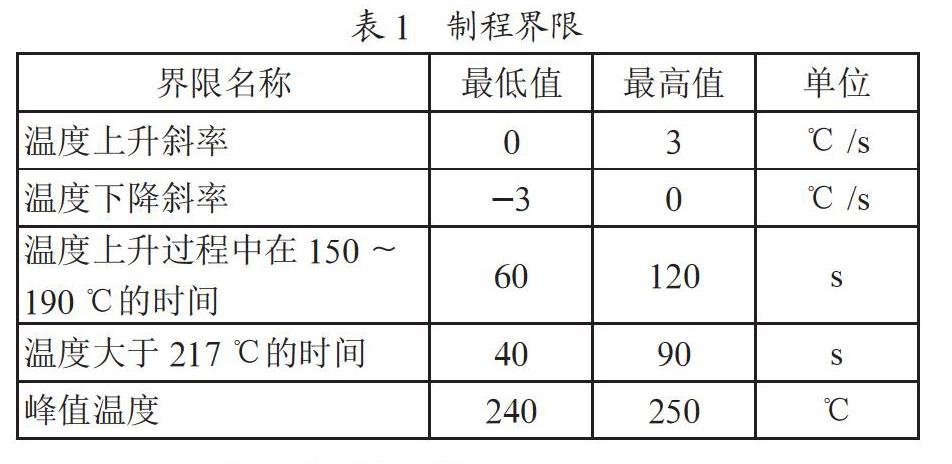
回焊炉启动后，炉内温度短时间稳定。间隙不做特殊控制，其温度与相邻温区的温度有关。实际生产时各小温区设定温度可以进行±10 ℃调整。调整时要求小温区1～5中的温度保持一致，小温区8～9中的温度保持一致，小温区10～11中的温度保持25 ℃。传送带的过炉速度调节范围为65～100 cm/min。在回焊炉电路板焊接生产中，炉温曲线应满足一定的要求，称为制程界限，如表1所示。

1.3  回焊炉内温度分析

小温区空气温度可视为均匀分布。沿着传送带方向焊接区域温度沿着传送带方向不尽相同。因此本文仅研究传送带中心环境的一维传热过程，将回焊炉分为如图1所示的三类区域：小温区对应传送带上的区域Di（i=1，2，…，11），间隙对应传送带上的区域Bj（j=1，2，…，10），单热源影响区域对应传送带上的区域Ck（k=1，2）。

2  模型的建立

2.1  模型构建思路

由于电路板温度与轨道焊接区域温度直接相关，而焊接区域温度又与两边小温区温度相关，则本文建模主要分两部分：

第一部分构建模型旨在设计回焊炉焊接区域不同位置的温度分布，考虑在热传导与热对流的两种热传递方式下，运用牛顿冷却定律以及傅里叶定律，构建炉内气体传热模型以及间隙环境传热模型。分别构建出小温区环境温度、间隙环境温度、炉前炉后环境温度模型并整合为环境温度分布模型。

第二部分构建模型旨在探究电路板温度与焊接区域温度之间的关系，由于回焊炉主要加热方式为小温区持续喷射出的热风与电路板直接的热传递，因此本文主要考虑对流传热，运用牛顿冷却定律，构建电路板温度变化差分模型。

综上所述绘制出本文模型构建的思维导图，如图2所示。

2.2  环境温度分布模型

2.2.1  小温区Di环境温度模型

小温区产生的热量持续向空气输入最终趋于平衡。则传送带中心位置气体温度Uat=Ui。Ui为第i个小温区温度。

2.2.2  间隙Bj的环境温度模型

由热力学定律可知，热量可以自发地从高温物体传给低温物体。工程上任何复杂的传热现象都是由传导导热、对流传热、热辐射三种基本传热方式组成[1]。间隙Bj的环境温度变化主要通过热传导和热对流产生。为探求间隙的环境温度变化，进行如下推导。

2.2.2.1  炉内气体传热

传送带不同区域上的温度变化是以气体作为介质，易热传导的方式热量交换。设两个小温区i、i+1温度分别为Ui、Ui+1（Ui+1>Ui），间隙的温度还未平衡时，由热力学第二定律，热量能够自发地从高温物体传递给低温物体。根据傅里叶定律：单位时间内流过单位横截面积的热量q与温度的下降成正比[2]。

（1）

其中，负号为热量流动方向与温度升高方向相反，λ为导热系数， 为温度沿x方向变化率。

如图3所示，设任意位置x0处t时刻的温度为U（x0，t），如图做两个垂直热流方向的横截面积ΔS。dt时间内通过x0+dx处ΔS横截面流入小柱体内的热量为：

流出小柱体内的热量为：

由上述两式可得dt时间内小柱体净流入量为：

（2）

由于，故可化简为：

（3）

记dV=ΔSdx，则dt时间内小柱体单位体积内的净热量为：

（4）

已知，热传导介质的密度为ρ，比热容为c，dt时间内引起小柱体单位体积温度升高所需的热量为dq=cρ（Ut+ dt-Ut），而dt时间内流入小柱体的热量即为使小柱体温度升高所需的热量由于，整理可得一维的热传导方程为：

（5）

当温区间的温度稳定后，温度将不随时间变化，因此炉内空气温度是关于位置的函数U（x），温度梯度  也不随时间变化。

2.2.2.2  间隙气体对流传热模型

通过气体对流进行热量交换的方式为热对流，其能量交换满足牛顿冷却定律[2]：

Q=Sα（Uat-U）                             （6）

其中，Uat为小温区焊接区域气体温度，U为间隙焊接区域气体温度，S为垂直高温气流方向的截面积，α为换热系数，反映对流换热程度的强弱。

由式（6）可知单位时间小温区焊接区域气体吸收的热量dQ=Sα（Uat-U）dt，与气体温度升高dU需要吸收的热量dQ=ρcVdU相等，即：

Sα（Uat-U）dt=ρcVdU                         （7）

式中，ρ為小温区焊接区域气体密度，c为小温区焊接区域气体比热容，V为电路板体积。设时间从t到t+dt时，温度从U1变化到U2，对式（7）两边同时积分得 ，两边同时求原函数并取对数得Uat-U1=（Uat-U2） 记 （τ>0），则：

U2=U1+（Uat-U1）（1-）                  （8）

根据以上推导，最终选择直线U（x）为间隙焊接区域气体温度分布：

U（x）=                 （9）

理由如下：式（9）满足传导传热规律，当温度不随时间变化，温度是关于位置的函数U（x），温度梯度  也不随时间变化;式中U（x）满足对流传热过程中的牛顿冷却定律;对于回焊炉内间隙长度为5 cm较小，用直线拟合产生的误差也较小;气体温度分布满足流体的连续介质假说[3]。

2.2.3  单热源影响区域Ck温度

单热源影响区域是指受单个热源影响的区域。由于单热源影响区域一边温度较高，热传导的能量会从另外一边散失的很快，该区域气体温度升高所需的能量的主要是通过对流换热，其温度变化应满足牛顿冷却定律。U0为生产车间的温度，Us为单热源的温度，Ux为距离单热源x位置处的气体温度，由式（8）可得温度在单热源影响区域的分布为：

Ux=Us+（U0-Us）（1-e-xψi）                 （10）

其中，ψi为第i个单热源对邻近区域温度的影响程度，其大小反映了介质导热能力的强弱，不同单热源影响的区域，参数ψi不同。

2.2.4  环境温度分布模型

根据上述模型的推导，联立式（9）（12）可得炉内环境温度在传送带上的一维分布：

（11）

2.3  炉温曲线差分模型

由于电路板附近热气流从小温区喷射出，最终到达电路板表面与其发生热传递。传送带周围的气体与电路板之间热传递的方式为热对流，则电路板表面温度应满足对流换热式（8）。

将式（8）写成差分形式：

（12）

其中，U（t）为t时刻电路板的表面温度，Uat（vt）为电路板在t时刻的位置所对应的环境温度，β为电路板与环境的换热系数。

实际电路板表面的温度随时间的变化有一定的滞后性[4]，即：

U′（t）=U（t-γΔt）=U（t-Δt-γΔt）+[Uat（vt-vγΔt）

-U（t-γΔt-Δt）]（1-）                      （13）

将此模型记为模型Ⅰ，式中，γ为电路板表面温度的延时常数。

3  参数确定

本文根据赛题中第一问数据：各温区设定的温度分别为175 ℃（小温区1～5）、195 ℃（小温区6）、235 ℃（小温区7）、255 ℃（小温区8～9）及25 ℃（小温区10～11），传送带的过炉速度为70 cm/min的实际与理论炉温曲线的偏离程度作为评判，利用实验数据调整炉温曲线差分模型中各参数，最终得到的ψ1=0.160，ψ2=0.014，ψ3=0.019，β=50，γ=2，最终理论与实际炉温曲线对比图如图4所示。

4  寻求最大过炉速度

实际生产过程中，电路板的过炉速度越快，则电路板焊接数量越多，效益越好。然而过炉速度并不能无限制增大，还需满足制程界限如表1所示。因此为了使效益最大化，本文选取各温区温度的设定值分别为182 ℃（小温区1～5）、203 ℃（小温区6）、237 ℃（小温区7）、254 ℃（小温区8～9）炉温曲线满足制程界限的情况下，寻求出符合要求的最大传送带过炉速度。

4.1  最大过炉速度模型建立

约束条件可由制程界限推导出。目标函数：需寻求出符合要求的最大传送带的过炉速度。则目标函数为：max v，v为传送带过炉速度。

最大过炉速度模型（模型Ⅱ）：

max v

（14）

其中，t1为第一次达到150 ℃对应的时间，t2为第一次达到190 ℃对应的时间， 为降温至150 ℃时间， 为降温至190 ℃时间。

4.2  最大过炉速度模型求解

4.2.1  搜索算法的构建

模型Ⅱ本质上是一个单变量最优化问题，提出一种搜索算法其过程为：

（1）确定初始搜索区间[v1，v2]，搜索步长为Δv;

（2）在搜索区间[v1，v2]内按步长Δv从大到小搜索，记录第一个满足约束条件的速度v;

（3）更新搜索区间[v-Δv，v+Δv]，并缩小搜索步长Δv，使其变为  ;

（4）重复步骤（2）、（3），直到Δv

上述算法流程图如图5所示。

以上算法初值与参数的设定：

传送带过炉速度调节范围为v∈[65，100]，初始搜索步长设定为1。参数n=10，即每次更新后步长变为原来的  ;参数p=10-4，即最终输出速度的精度为10-4。

4.2.2  模型Ⅱ运算结果

模型Ⅱ通过以上搜索算法利用Matlab软件编程求解，得到允许的最大传送带过炉速度为：

vmax=75.76 cm/min

5  最优炉温系统设计

理想的炉温曲线还应使超过217 ℃到峰值温度所覆盖的面积尽可能小，进一步还希望以峰值温度为中心线的两侧超过217 ℃的炉温曲线应尽量对称。因此合理调节回焊炉各个温区温度，既能保证电路板的焊接质量，又能使得效益最大化。

5.1  最优炉温系统模型建立

首先要求在制程界限求出最优炉温曲線以及其对应各温区设定温度、传送带过炉速度即可得对应约束条件。各温区最合适温度表示为Ub=[Ub1，Ub2，Ub3，Ub4]，其中Ub1∈[165，185]表示小温区1～5的设定温度，Ub2∈[185，205]表示小温区6的设定温度，Ub3∈[225，245]表示小温区7的设定温度，Ub4∈[245，265]表示小温区8～9的设定温度。最合适的传送带速度为vb。

目标函数的确定：

设A为超过217 ℃到峰值温度所覆盖的面积，ta为第一次到达217 ℃的时间，tb为温度到达峰值的时间，则覆盖面积为：

令Δt=，则原式表达为：

（15）

为描述两边曲线的对称程度，令（Ti，Ui）与（ti，ui）分别是差分方程U′（t）上距离对称轴（峰值所在的x轴垂线）最近的第i个点。当Δx较小时，Ti与ti重合，要使得峰值温度两侧超过217 ℃炉温曲线尽可能对称，即是使得|Ui-ui|足够小，则：

Ui-Ui+1≈ui-ui+1                           （16）

由式（16）可得 ，εi为第i个方程的偏差。方程偏差越小，说明中心线两边曲线的对称性越好。根据方差的定义，该方程每一个偏差越小说明偏差的方差也越小。即研究对称性目标函数为：

（17）

为建立更合理的评价指标，本文将综合考察曲线对称性和面积大小两个因素。

将炉温曲线超过217 ℃到峰值所覆盖的面积映射到[0，1]，消除量纲的影响，避免面积的数值远大于斜率偏差方差所造成的“大数吃小数”现象，所以面积大小比率为：

（18）

此外，由于焊接材料熔点为217 ℃左右，温度在217 ℃到峰值温度覆盖的面积意义在于：若电路板温度高于217 ℃时间过短或者温度峰值太低会导致焊接材料融化不完全，焊接效果较差;若电路板温度高于217 ℃时间过长或温度峰值太高会导致焊接材料最终融化为液体四处流动，焊接效果较差。然而，使得超过217 ℃的炉温曲线尽可能对称的意义在于焊接材料不会发生骤冷或者骤热，从而避免焊接材料由于降温太慢或太快导致其最终形成的焊接材料韧性太差或者脆性太强，实际材料的骤冷骤热对材料的性能虽有影响，但影响并不是很大。权衡上述两方面因素，材料温度条件的重要性高于超过熔点部分炉温曲线的对称条件。所以衡量炉温曲线优劣程度的指标Assess，取权重为ω1，ω2作为衡量这两个因素的重要性，本文取ω1=0.7，ω2=0.3。最终，得到综合评价指标：

Assess=0.7η+0.3σ                          （19）

其中，面积大小比率η由式（18）求得，斜率偏差方差σ由式（17）求得。

则计算超过217 ℃到峰值温度的最小覆盖面积的模型Ⅲ为：

minAssess=0.7η+0.3σ

（20）

5.2  最优炉温系统模型求解

本文使用退火算法求解，其优点在于其会按照一定概率跳出局部最优，以达到寻找全局最优解的目的，并且算法收敛速度很快，用于求解多变量组合优化问题十分有效。通过退火算法，运用计算机求解，可得各温区对应下的最优温度和传送带过炉速度如表2所示。

计算出斜率偏差方差σ=0.533 6，面积比率η=0.583 8，模型的评价指标为Assess=0.568 7。对应炉温曲线如图6所示，其中虚线是电路板已经离开回焊炉或已经通过回焊炉。

6  结  论

本文针对一种型号的回焊炉的炉温曲线进行研究，首先根据机理构建了一维的炉温曲线差分模型，使用一次实验测量的数据进行模型各参数的调整后，模型的理论炉温曲线与实际炉温曲线基本重合，因此本文模型较为精确。在模型精确的前提下，进一步使用搜索算法，蒙特卡洛法以及模拟退火算法全局寻优，寻求出了使得经济效益最大时对应的试件的最大过炉速度以及各温区应被控制稳定的温度。

因此，若要探究其他型號回焊炉的最优炉温系统，只需测量一次该种型号回焊炉炉温曲线，然后根据实验数据调整本文模型内各参数，本文模型即可适用于该种回焊炉。若制程界限有所不同，对应调节本文模型Ⅱ与模型Ⅲ的约束条件，采用相同的研究方法即可设计出不同型号回焊炉对应的最优炉温系统。

参考文献：

[1] 汪学军.多温区自动测控系统控制模型的建立与研究 [D].长沙：中南大学，2007.

[2] 张玉民.热学：第2版 [M].北京：科学出版社，2006.

[3] 360百科.连续介质 [EB/OL].[2020-09-13]. https：//baike.so.com/doc/897475-948678.html.

[4] 高金刚.表面贴装工艺生产线上回流焊曲线的优化与控制 [D].上海：上海交通大学，2007.

作者简介：方灏航（1999.05—），男，汉族，湖北黄冈人，本科在读，研究方向：机械工程。