矩-面积定理的拟图乘法证明及局部图乘法导出

阙仁波

(厦门大学嘉庚学院土木工程分院 福建漳州 363105)

0 引言

矩-面积第一定理和第二定理是直接从梁的挠曲线近似微分方程出发，将积分表达式从梁的挠曲线几何性质角度进行解释，从而求出弯矩图面积和面积矩来代替直接求积分而求解两截面间由于弯曲所引起的相对转角和相对挠度的方法[1-6]。若两截面中其中一个的绝对转角或绝对挠度为已知，则可以之为参考点，其绝对转角和绝对挠度为两截面之间的刚体转动和刚体平动，容易求得由它们所引起的、待求截面处的转动和平动，再叠加上相对转角和相对挠度，即可得待求截面处的绝对转角和绝对挠度。但该方法在运用时，往往存在为确定方向而要画变形示意图和建立局部坐标系的麻烦。

图乘法亦是将积分表达式从弯矩图的几何性质角度进行解释，从而以求两个弯矩图的几何参数之积来代替直接求积分、以求解由于弯曲所引起的两截面间的相对转角和相对挠度或指定截面处的绝对转角和绝对挠度的方法[7]。但该方法必须对结构的所有构件都进行图乘，计算量较大。

为此，本文先采用拟图乘法对矩-面积定理进行证明，找出两者的统一性。并将两者的思想相融合，导出局部图乘法。采用该方法，对于某些问题，可在一定程度上减少了上述两种方法各自的麻烦和计算量。

1 矩-面积定理简介

1.1 矩-面积第一定理

光滑连续弹性挠曲线上任意两点的转角之差，等于M/(EI)图中这两点间曲线所围的面积[1-5]。

如图1(a)和(b)所示：

(1)

其中，AAB表示M/(EI)图中AB段的面积，它前面的负号表示正的弯矩面积将引起两点间产生逆时针方向的相对转角，即:B点切线相对于A点切线逆时针转动。

1.2 矩-面积第二定理

光滑连续弹性挠曲线上B点相对于A点切线的偏移量tB/A，等于M/(EI)图中A、B两点间曲线所围的面积对过B点铅垂线的静矩[1-5]。

如图1(a)和(b)所示：

(2)

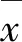
图1 挠曲线、M/(EI)图和M图

2 图乘法证明

2.1 位移的分解

如图2(a)所示，可设想将杆件从AB变位到A′B′的过程分解为有先后顺序的3个，即沿竖向刚体平动ωA到A′B″、然后刚体转动θA到A′B‴、再变形即相对侧移ΔωB/A和相对转动ΔθB/A到A′B′，则：

θB=θA+ΔθB/A

(3)

在小变形情况下：

ωB=ωA+θAlAB+ΔωB/A

(4)

注：图2(a)中之所以让B′点位于A′B‴下方而不是像图1(a)中让B点位于AC上方，主要是为了让几个位移之间不相重叠，看起来更清楚，更便于阐释。

图2 位移的分解

2.2 类比与证明

若不考虑刚体平动和转动，以A′B″为基线重绘图2(a)可得图2(b)。

根据前述正负号的规定，由图1(a)可得：

θB=θA+θB/A

(5)

ωB=ωA+θAlAB+tB/A

(6)

对比式(3)和(5)、式(4)和(6)、以及图1(a)和图2(b)可得:

ΔθB/A=-θB/A

(7)

ΔωB/A=-tB/A

(8)

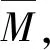
(9)

负号表示方向与施加的单位力偶相反，即逆时针。

图3 B端单位力偶所引起的弯矩图

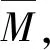
(10)

图4 B端单位竖向力所引起的弯矩图

负号表示方向与施加的单位力相反，即从C点到B点沿y轴负向。

由上述可看出，矩面积第一定理和第二定理，亦可按拟图乘方式推导得出，但与要对所有构件都进行图乘的通常的图乘法(在此不妨称之为全局图乘法)相比，拟图乘法仅对要求相对转角和相对挠度的A点和B点之间的节段进行图乘，且将AB段看成是一端固定的悬臂梁，故在此不妨称之为局部图乘法。

但需注意，图4和图1(c)中AB段图乘的结果与图5和图1(c)中AB段图乘的结果(等于tA/B)一般不相等，故一般tB/A≠tA/B。

图5 A端单位竖向力所引起的弯矩图

由式(4)可见，若ωB=ωA=0，如支座在A点和B点处的简支梁或伸臂梁、或A点和B点处无垂直于杆轴向侧移的刚架杆等，则：

θA=-ΔωB/A/lAB

(11)

即此时可将θA的求解转换为tB/A的求解。

3 局部图乘法的实施步骤和应用要点

由上述可得到启示，可将矩-面积定理改用局部图乘法来实现。实施步骤和应用要点如下：

(1)B点相对于A点的转角之差ΔωB/A，可由实际荷载作用下A点和B点之间的弯矩图(图1(c))，与将A端固定、B端自由的悬臂梁在B端施加单位力偶所产生的弯矩图(图3)进行图乘而得到。若所得结果为正，则表示B点切线相对于A点切线的转动方向与单位力偶同向；反之，反向。

(2)B点相对于A点切线的偏移量ΔωB/A，可由实际荷载作用下A点和B点之间的弯矩图(图1(c))，与将A端固定、B端自由的悬臂梁在B端施加垂直于杆轴向的单位力而产生的弯矩图(图4)进行图乘而得到。若所得结果为正，则表示从A点切线与经过B点的垂线交点(图1(a)中的C点)到B点的偏移方向与施加的单位力同向；反之，反向。

(3)若ωA=ωB=0，则欲求解θA时，可按上述(2)的方法先求得ΔωB/A，再按式(11)求θA，负号表示θA沿从AB转向AC的方向。因为ωB=0，故可根据ΔωB/A的正负确定出C点位于AB的哪一侧，然后由AB到AC的转向，即为θA的转向。

若已知参考点A处的θA和ωA，则可进一步通过式(3)和(4)求得B处的绝对转角和绝对挠度。

由于同一刚结点处的各根杆件的转角相同，故，如图6所示，对处于同一直线上的两根杆件，求ωB用式(4)，而求ωB′则用：

ωB′=ωA-θAlAB′+ΔωB′/A

(12)

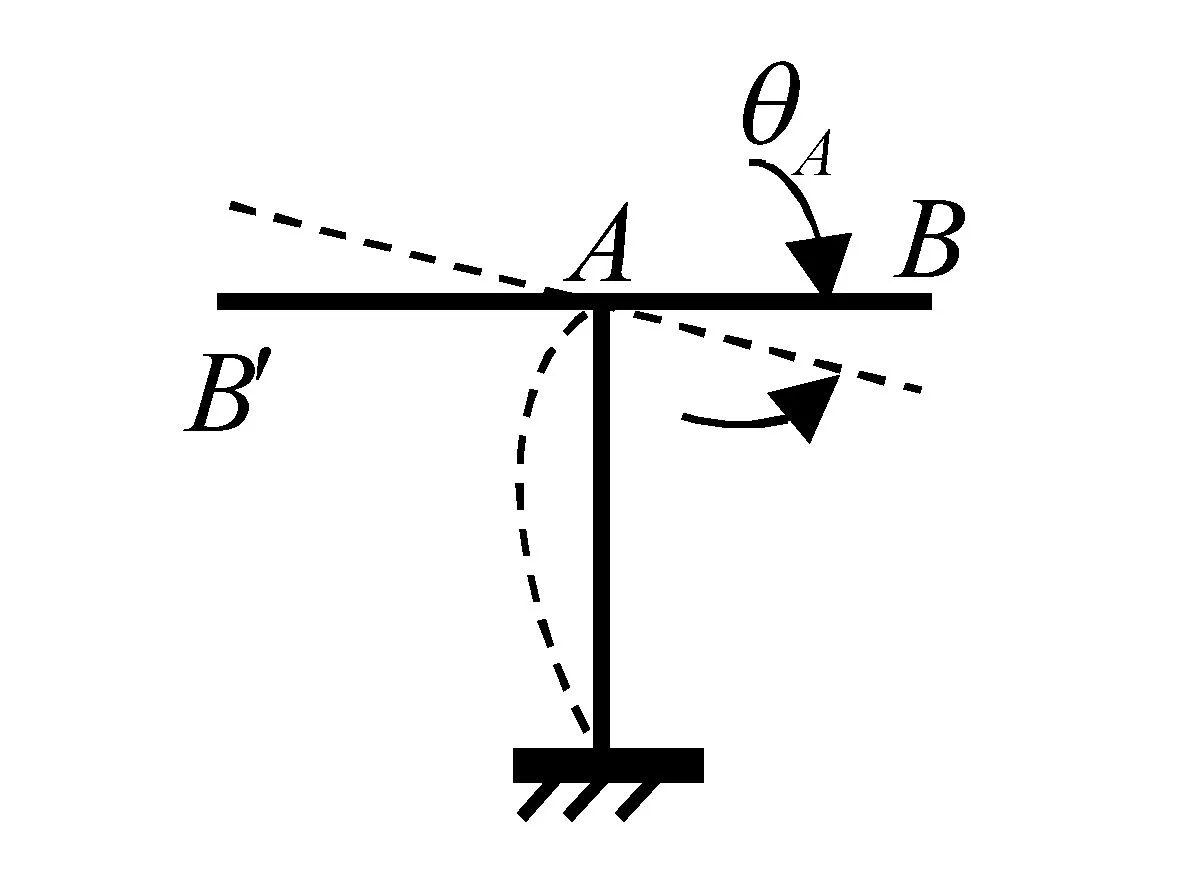
图6 刚体转动引起的位移示意图

4 示例

4.1 例1

计算图7(a)所示结构中的θA和ωc，设杆件的截面抗弯刚度为EI。

解：将图7(b)的AB段弯矩与图7(d)的弯矩进行图乘，可得：

将图7(b)的AC段弯矩与图7(f)的弯矩图乘，可得：

/(EI)=10Fa3/(3EI)(↓)

由式(4)可得：

ωC=ωA+θAlAC+ΔωC/A=-Fa2/(2EI)×4a+10Fa3/(3EI)=4Fa3/(3EI)(↓)

图7 例1的结构受力图和弯矩图

4.2 例2

计算图8(a)所示结构中的θB和ωC，设各杆件的截面抗弯刚度均为EI。

解：将图8(b)的AB段弯矩与图8(d)的图乘可得：

图8 例2的结构受力图和弯矩图

忽略杆件轴向变形,则由于BC和CE的水平向支撑，AB杆中B点无垂直于杆轴向的位移，即ωB=0，又ωA=0，故由式(11)可得：

将图8(b)中的BC段弯矩与图8(f)的图乘可得：

忽略杆件的轴向变形,则由于AB杆的竖向支撑，BC杆中的B点无垂直于杆轴向的位移，即ωB=0，又因为同一刚结点处各杆件的转角相同，故由式(4)可得：

ωC=ωB+θBlBC+ΔωC/B=Fa2/(3EI)×a+Fa3/(6EI)=Fa3/(2EI)(↓)

4.3 例3

图9(a)所示的超静定刚架，已通过力法求解得到了其弯矩图，横梁和立柱的截面抗弯刚度分别为2EI和EI[7]。试进一步求θB、θC和ωG。

解：将图9(a)的BD段弯矩与图9(b)的图乘可得：

又θD=0，故:

将图9(a)的BC段弯矩与图9(c)的图乘可得：

图9 例3的结构受力图和弯矩图

将图9(a)的GB段弯矩与图9(d)的图乘可得：

忽略杆件的轴向变形，则由于杆件BD的支撑，BG杆件中ωB=0，故应用式(12)可得：

ωG=ωB-θBlBG+ΔωG/B=-θBlBG+ΔωG/B

=-(-40)/(EI)×2-25/(EI)=55/(EI)(↓)

4.4 例4

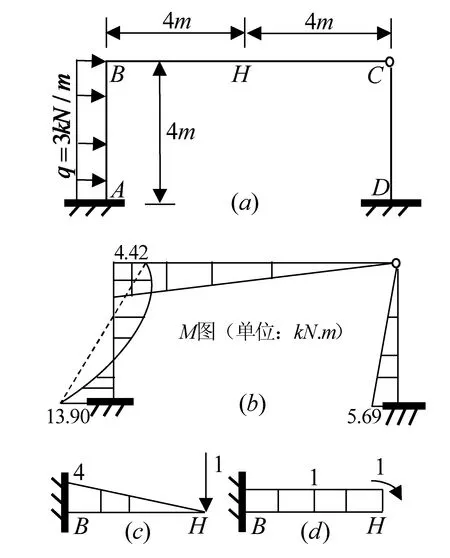
图10 例4的结构受力图和弯矩图

解：忽略杆件的轴向变形，则由于BA杆的竖向支撑，在BC杆中的B点处无垂直于杆轴向的位移，即ωB=0，又因为θB已通过位移法求出，故可选B点作为参考点来求BC跨中任一点的绝对转角和挠度。

将图10(b)的BH段弯矩与10(c)的图乘可得：

将图10(b)的BH段弯矩与10(d)的图乘可得：

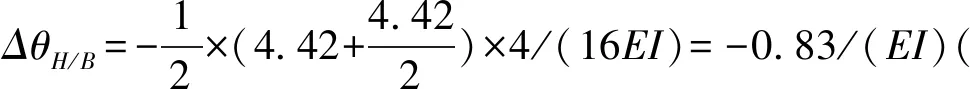
ωH=ωB+θBlBH+ΔωH/B=θBlBH+ΔωH/B=(0.737×4-1.84)/(EI)=1.11/(EI)(↓)

5 结论

基于采用拟图乘法证明了矩-面积第一定理和第二定理，并导出了局部图乘法；通过例子展示了局部图乘法的应用；局部图乘法不仅可用于静定结构，若与力法或位移法相结合，还可用于超静定梁和刚架；可总结出局部图乘法具有如下特点：

(1)转角和挠度的方向只需根据最后求得的结果的正负号并结合在悬臂梁上施加的单位荷载方向，即可确定，无需像矩-面积定理一样要靠画变形示意图和建立如图1(a)所示的坐标系，然后根据式(1)和(2)中正负号的含义来判断。

(2)如例题所示，辅以适当的分析，很多问题可转化为用局部图乘法来求解，相比全局图乘法，计算量可减少，毕竟图乘中经常会涉及诸如求面积、求形心位置和对应的坐标、分段和分块等繁琐的工作。

(3)联合力法或位移法，可用于求解超静定梁和刚架的位移。

(4)在求绝对转角和绝对挠度时，全局图乘法无需选择参考点，因为它已包含了刚体平移和刚体转动；而局部图乘法和矩-面积定理一样，要选择参考点，后两种方法中，刚体位移与变形的概念泾渭分明。

(5)尽管相比矩-面积定理多了一些画单位力和力偶作用下的弯矩图，但对于悬臂梁而言，却非常方便。