基于综合应力的电子产品寿命预测仿真方法研究*
2020-05-18栾家辉朱兴高代永德
栾家辉,朱兴高,陈 皓,代永德
(中国航天标准化研究所,北京 100071)
0 引言
卫星电子产品在发射以及在轨条件下受到振动、温度、太阳辐照和通电等综合作用,对产品的寿命产生较大影响。而电子产品作为航天型号多个系统中的重要组成部分,具有分布广泛、功能集成度高、运行环境恶劣的特点,其寿命与可靠性一直是人们关注的重点内容。随着星上电子产品在轨的寿命要求不断提升,产品开展1∶1的寿命试验越来越困难,试验周期和成本都难以保证,试验覆盖的环境工况也相对有限。利用仿真方法开展寿命预测是一种有效的手段,可以针对试验条件难以覆盖的工况进行仿真研究,暴露产品的薄弱环节。因此,开展综合应力下的星载电子产品寿命仿真预测具有重要意义。
1 寿命预测流程
为了克服电子产品试验条件难以覆盖典型在轨工况、薄弱环节无法暴露、综合应力条件无法施加的技术缺陷,解决产品在设计过程中并未充分开展寿命与可靠性仿真和试验验证工作,并且对发射过程和在轨环境的研究并未完全深入等问题,提出一种多应力综合下的卫星电子产品寿命预测方法,具体流程见图1。
1.1 典型应力条件特征分析
根据产品设计参数及其在发射与在轨过程中的各种环境和载荷条件,重点分析振动、热应力和电应力参数的量级。振动应力是指电子产品在发生振动和冲击环境下的力学承受能力,在振动疲劳效应和共振现象中,产品出现力学余电性能下降、零部件失效、疲劳损伤甚至损坏的现象;在温度环境条件下,产品中的器件会出现性能参数的偏差乃至失效,产品封装结构由于材料膨胀系数不同导致变形不均匀而产生明显的断裂;电路板上的元器件因经历着内部电流和外部环境的影响而极易发生性能退化和失效。
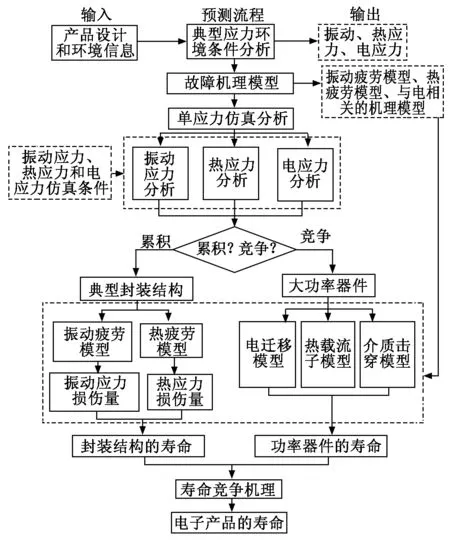
图1 电子产品寿命预测流程
1.2 故障机理模型分析
调研分析了电子产品在综合应力下的振动疲劳、热疲劳、电迁移、热载流子、介质击穿等故障机理模型。
1.2.1 与振动应力相关的机理模型
不考虑温度时的振动疲劳模型为:
(1)
其中:Nf为器件在振动疲劳故障前的应力循环次数;C为根据标准试验确定的常数,对于随机振动,C=2×106;x和y为该器件在电路板上的位置坐标;b为疲劳强度指数;z1和z2为产品结构系数,由最大功率谱密度和结构尺寸决定,功率谱密度可仿真求得。
考虑温度时的振动疲劳模型为:
(2)
其中:Nf(T)为不同温度下器件在振动疲劳故障前的应力循环次数;Δε(T)为总应变量,仿真求得;E(T)为弹性模量;σ0(T)为平均应力;σf(T)为应力强度,仿真求得;c为疲劳韧性指数;εf(T)为疲劳韧性系数,查材料参数表得出;T为温度。
1.2.2 与热应力相关的机理模型
热疲劳机理模型为:
(3)
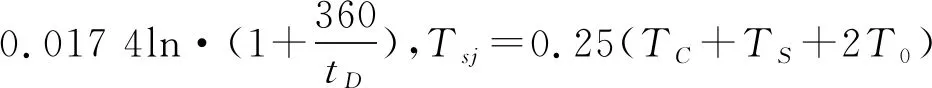
1.2.3 与电应力相关的机理模型
与电应力相关的机理模型包括电迁移(Electro-Migration,EM)、热载流子(Hot Carrier Injection,HCI)和介质击穿(Time Dependent Dielectric Breakdown,TDDB)模型。其中,电迁移模型适用于多晶程度高和晶体结构较为无序的铝薄膜器件;热载流子模型适应于金属氧化物半导体场效应晶体管;介质击穿模型分为两种模型,均适用于硅器件。器件失效前时间用TTF(Time to Failure)表示。
(1) 电迁移模型为:
(4)
其中:w为芯片金属化层的宽度;t为芯片金属化层的厚度;J为金属化层的电流密度,仿真求得;Ea为激活能;k为波尔兹曼常数,k=1.381×10-23J/K;C1为与金属的几何尺寸和温度有关的参数。芯片金属导线不同横截面积下C1、Ea的取值通过查材料参数表得出。
(2) 热载流子机理模型为:
(5)
其中:Id为漏电流;Isub为衬底电流,仿真求得;W为沟道宽度;H、m为两个拟合的参数,常取m=2.85,H=100。
(3) 介质击穿机理模型分为热化学退化模型和空穴诱生击穿模型。
热化学退化模型为:
(6)
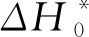
空穴诱生击穿模型为:
(7)
其中:t0为常数,t0=10-11s;G为空气的击穿场强度,G=350 MV/cm;Q为电荷量,Q=0.3 eV。
电子产品的故障机理模型由于环境条件和自身结构组成的不同而呈现出多样性,机理模型分析为后续产品的寿命预测提供了理论基础。
1.3 单应力仿真分析
根据应力条件特征分析结果,开展单应力仿真分析,获得振动应力、热应力和电应力的分析结果。
(1) 振动应力仿真分析流程如图2所示。
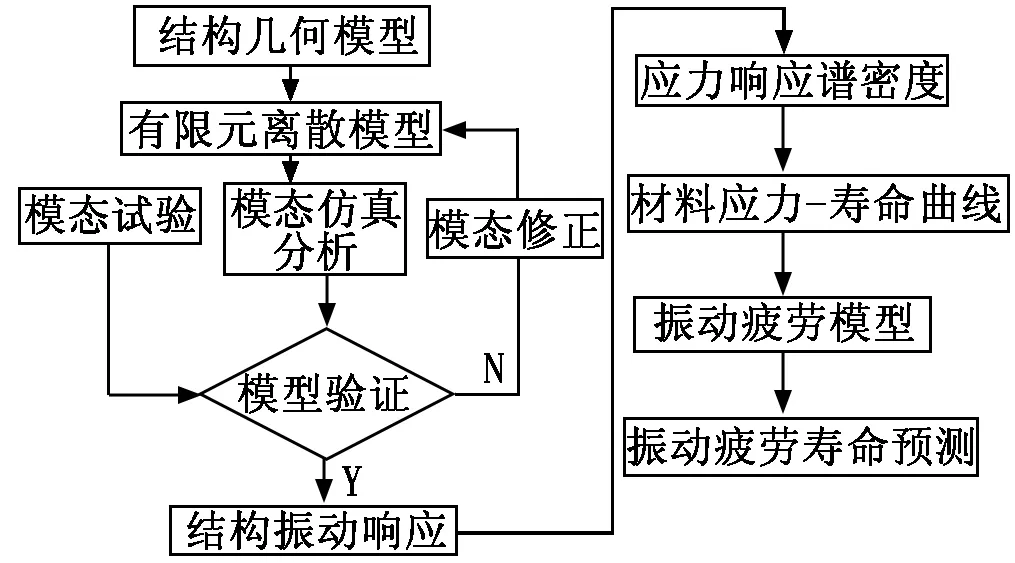
图2 振动应力仿真分析流程
电子产品在随机振动条件下的寿命仿真重点关注封装结构件的有限元模型简化与模型修正、危险部位应力响应谱密度提取方法、材料-寿命曲线的正确性和适应性。对结构进行响应分析,得到外载荷作用下结构危险部位和随机振动分析的响应结果,为后续将振动分析结果代入振动疲劳模型提供输入条件。
(2) 热应力仿真流程如图3所示。
电子产品在热应力条件下的寿命仿真重点会考虑封装结构的典型材料和结构(如引脚、引线和焊点等)组成在高低温下的热变形和热应力,在交变热载荷作用下的热疲劳,为后续将热应力分析结果代入热疲劳模型提供输入条件。
(3) 电应力仿真流程见图4。
电子产品在电应力条件下的寿命仿真为:建立器件模型,对该模型进行仿真,输出元器件对电流、电压的承受能力,通过与器件手册或者实验数据进行对比,使器件满足设计要求。在器件模型符合要求的基础上,根据电路原理图,开展电路建模,对电路性能进行仿真,找出影响产品寿命的关键参数,输出薄弱环节,为后续将电应力分析结果代入电迁移等模型提供条件。
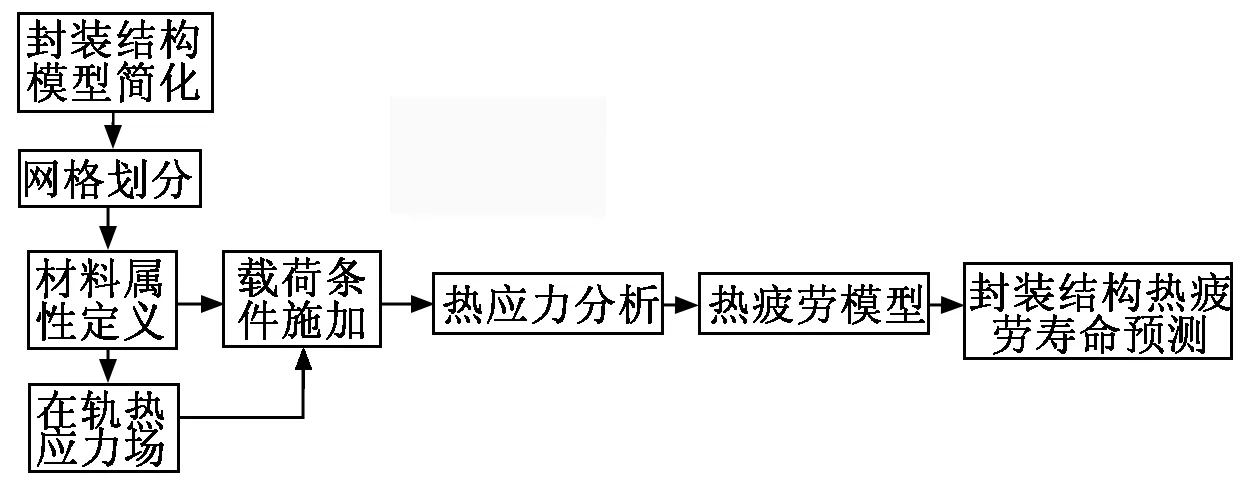
图3 热应力仿真分析流程
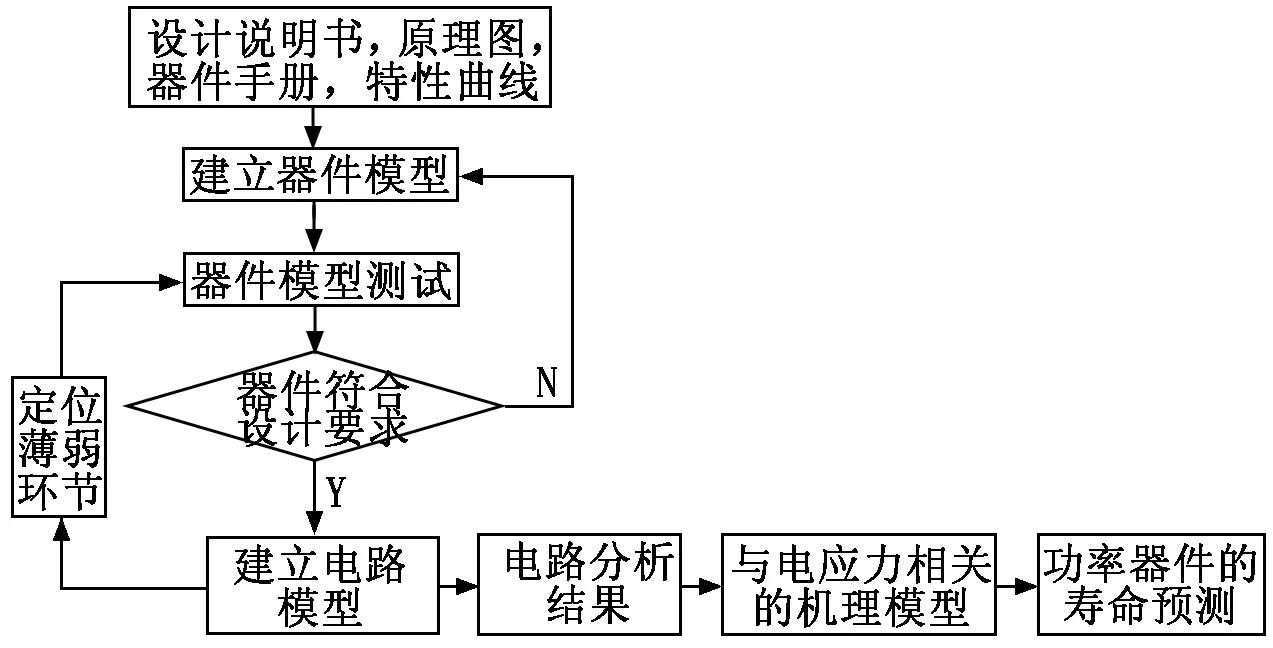
图4 电应力仿真分析流程
1.4 寿命预测方法
(1) 针对属于封装结构的部件,利用仿真得到的随机振动分析结果、热分析结果,采用振动疲劳模型和热疲劳模型求得结构的振动疲劳和热疲劳故障前的应力循环次数,提出采用热与振动同时作用下的累积损伤模型开展封装结构的寿命计算。
在振动应力损伤方面,采用考虑温度时的振动疲劳模型计算出不同温度下振动疲劳故障前应力循环次数,利用公式(8)求出振动应力下损伤量:
(8)
其中:Dv(total)为振动引起的总损伤量;Dv(T)为不同温度下的振动损伤量;fj为不同温度时间所占总时间的百分比。
在热应力损伤方面,采用热疲劳模型计算出热疲劳故障前的应力循环次数Nf1,利用公式(9)求得热应力下的损伤量Dth:
(9)
将结构的振动应力损伤量和热应力损伤量求和得到总损伤量,其倒数就是封装结构的疲劳寿命。总损伤量为:
Dtotal=Dv(total)+Dth.
(10)
则电子产品封装结构的疲劳寿命为:
(11)
(2) 针对功率器件,依据电应力仿真结果确定电路的薄弱环节,利用与电应力相关的机理模型计算器件寿命,采用竞争失效原则来处理,即最短故障前时间认为是器件的寿命。
(3) 电子产品的寿命通过在振动、热应力所造成的疲劳损伤和电应力引起的故障之间的竞争来确定,薄弱环节的寿命就是电子产品的整机寿命,至此完成电子产品的寿命预测。
2 典型案例应用
以某星载计算机的电路板(如图5所示)为例,开展典型案例应用。
经调研分析,电路板通电过程中同时受到随机振动和温度循环的综合应力作用,振动加速度均方根为6.65g,温度循环条件为-40 ℃~60 ℃;电路板的封装结构在随机振动和温度循环下的故障机理为振动疲劳和热疲劳,功率器件的故障机理为电迁移和热载流子和介质击穿等。

图5 计算机电路板
根据电路板的三维模型和输入条件,收集大量元器件的尺寸、位置、封装材料、管脚形状、焊点尺寸等参数,元器件的故障模式影响分析严酷度等级应为III级(严酷度等级I级为系统功能丧失和人员伤亡;II级为系统功能丧失,无人员伤亡;3级为系统性能退化)以上。
构建电路板的单应力仿真模型,如图6所示。图6中,U01,U02,…,U30为电路板设计时针对元器件做的编号,表示元器件在电路板上的位置。
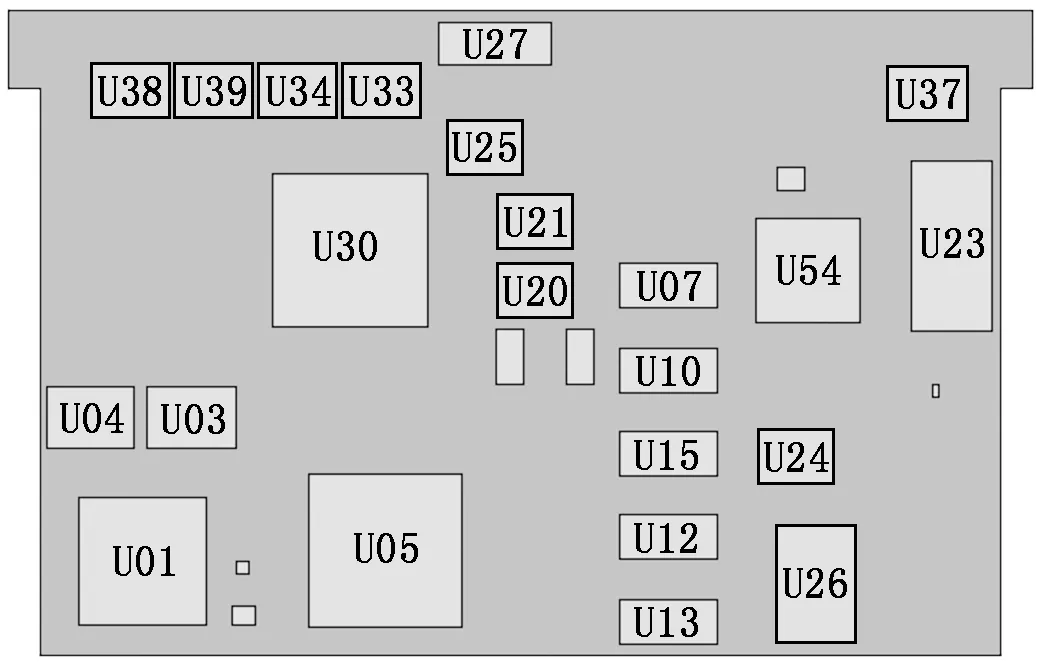
图6 电路板仿真模型
开展单应力仿真分析,得到振动和温度条件下的仿真结果,如图7和图8所示。
选择合理的故障机理模型,开展电路板的寿命预测,预测结果如表1、表2和表3所示。
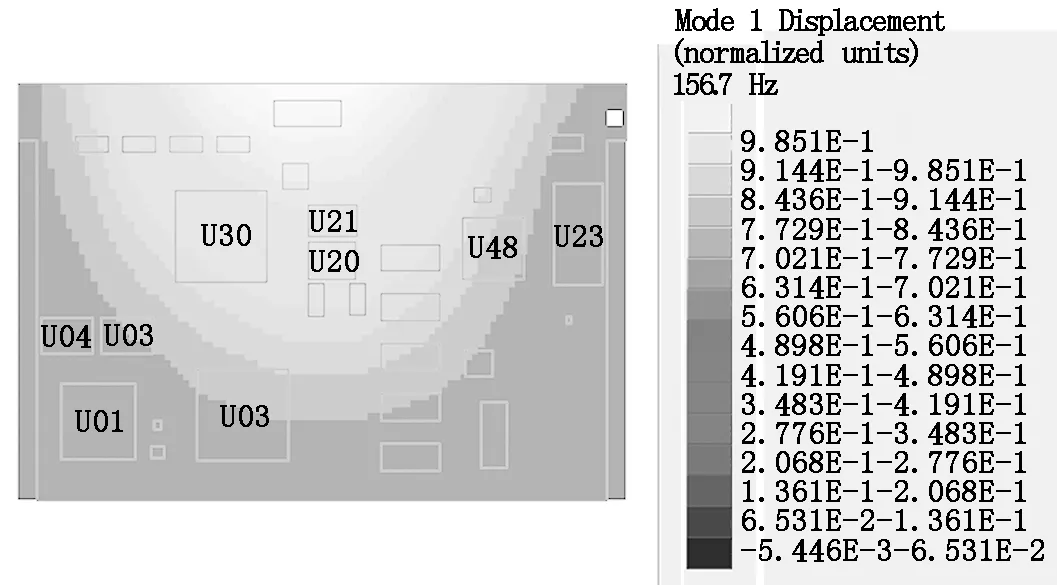
图7 振动应力分析结果

图8 热应力分析结果

表1 随机振动应力下的寿命预测结果

表2 热应力下的寿命预测结果
对于封装结构类,在振动和温度共同作用下的寿命预测结果如表4所示。
电应力作用下的功率器件寿命预测采用竞争失效原则,功率器件的寿命为16.43年;而对于整个电路板而言,考虑封装类结构寿命与功率器件寿命,根据竞争原则,最薄弱的寿命为整个电路板的寿命,为12.76年。
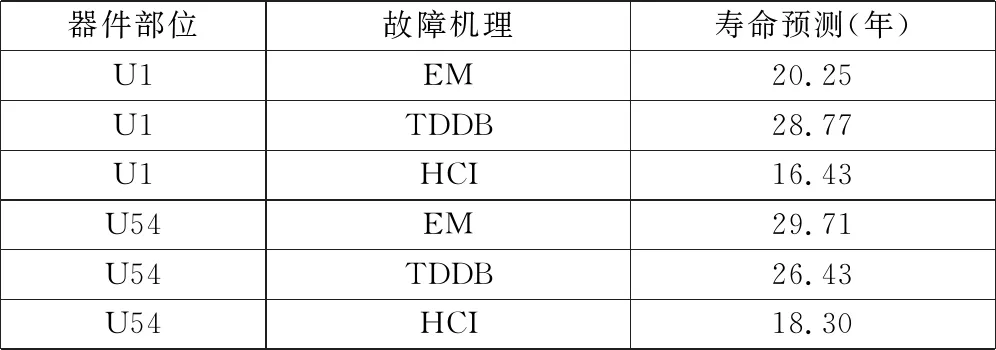
表3 电应力下的寿命预测结果

表4 振动与温度共同作用下的寿命预测结果
3 结束语
依据产品的综合应力条件特征,开展单应力仿真分析,根据产品寿命的累积损伤与竞争失效原则,提出了一种新的寿命预测仿真方法,给出了预测流程,并开展了典型产品的工程实例验证,有效节省了电子产品寿命评估的时间和成本,大大提高了寿命预测的准确度。
