SOA优化BP神经网络的水体氨氮预测模型①

潘 赢， 贾国庆， 郜伟伟

(1.青海民族大学物理与电子信息工程学院，青海 西宁 810007；2.中国科学院上海微系统与信息技术研究所无线传感网与通信重点实验室，上海 200050)

0 引 言

神经网络(Neural Network，NN)作为一种较新的数据融合方法，在水环境监测、水质参数预测等领域具有较广泛的使用。然而，神经网络仍然有网络训练易陷入局部极小值等问题，导致其预测精度不高。因此，实际应用中常常与其他优化算法进行结合以获得更优的结果[1-5]。

众多的研究表明，不断提高预测精度是人们追求的目标，与众多优化算法结合获得更高精度是一个有效的途径。本文提出一种混合海鸥优化算法(Seagull Optimization Algorithm，SOA)[6]和BP(即反向传播)神经网络的氨氮预测模型，通过使用具有较优全局和局搜索能力的海鸥优化算法来优化BP神经网络结构，再使用优化后的模型对水体氨氮进行预测。仿真结果表明，本文提出的优化算法可获得比传统BP神经网络算法更高的预测精度。

1 改进BP神经网络氨氮预测模型

1.1 BP神经网络

神经网络的种类众多，而其中BP神经网络使用最为广泛。主要思想为将学习分为信号的正向传播和误差的反向传播。在学习过程中，样本输入通过输入层输入，通过隐含层神经元的运算处理后，传向输出层，而后求取输出层的实际数据与预测数据的误差，将误差进入反向传播阶段。在反向传播过程中主要基于梯度下降策略不断调整各层神经元之间的连接权值及隐含层和输出层节点的阈值，直到最终预测值与实际值的偏离满足要求。

BP神经网络的模型如图1所示。假设BP神经网络模型中输入层有d个神经元，有一个隐含层共g个神经元，输出层有l个神经元。

图1 BP神经网络模型

输入为Xi=[Xi1，Xi2,…,XiN]T，其中i=1，2，···,d，N为样本总组数，输出为Yj，其中j=1，2，…,l，输入层的第i个神经元到隐含层第h个神经元的连接权重为Vih，隐含层第h个神经元阈值为θh。则隐含层第h个神经元的输入为

(1)

BP神经网络中隐含层转移函数为S型函数，即

(2)

隐含层的第h个神经元的输出为

Bh=f(Ah-θh)

(3)

隐含层的第h个神经元与输出层第j个神经元的连接权值为Whj，阈值为θj，则输出层第j个神经元的输入为

(4)

输出层的传输函数也选择S形函数，则得到输出层第j个神经元输出为

Yj=f(Cj-θj)

(5)

假设输出层第j个神经元的实际值为Rj，则第j个神经元误差Ej可由下式计算获得

(6)

网络输出总误差为

(7)

BP神经网络采用梯度下降法来调整网络的权值和阈值以获得较优的输出。将误差展开至隐含层有

(8)

进一步将误差展开至输入层有

(9)

隐含层的第h个神经元与输出层第j个神经元的连接权值变化量可以由输出节点的误差及输出层和隐含层的权值表示如下

(10)

其中η为学习率。Whj首先影响的为输出层第j个神经元的输入，进而影响输出，而后才是最终整个网络的误差，因此有下式

(11)

根据前面所述有

(12)

根据S函数的性质：

f′(x)=f(x)·(1-f(x))

(13)

则有

(14)

继而权值变化量为

ΔWhj=ηgjBh

(15)

权值的调整公式如下

Whj(n+1)=Whj(n)+ΔWhj

(16)

n=1,2,…,N-1为样本组数，阈值变化量用下式表示

(17)

阈值的调整公式如下

θj(n+1)=θj(n)+Δθj

(18)

同理，输入层的第i个神经元到隐含层第h个神经元的连接权值变化为

(19)

其中

(20)

权值的调整公式如下

Vih(n+1)=Vih(n)+ΔVih

(21)

阈值变化为

Δθh=-ηeh

(22)

阈值调整为

θh(n+1)=θh(n)+Δθh

(23)

综上，BP神经网络算法流程可总结如下图2所示：

1.2 海鸥优化算法

海鸥优化算法是Gaurav Dhiman提出的一种新的全局搜索算法，启发于海鸥的迁移和攻击行为，与常见的几种优化算法比具有更好的优化性能[15]。本文主要研究海鸥的迁移和进攻两种自然行为。

1.2.1 迁移

在海鸥迁移过程中，该算法模拟海鸥群如何从一个位置移动到另一个位置。在这个阶段，每一个海鸥应该满足三个条件：

1)避免碰撞

避免邻居(即其他海鸥)之间的碰撞。一个附加变量A用于计算新的位置

(24)

A=fc-(x×(fc/Maxiteration))

where:x=0,1,2,…,Maxiteration

(25)

图2 BP神经网络算法流程图

其中引入fc控制变量A的范围，变量A从fc线性减小到0。

2)向最佳位置方向移动

在避免了相邻海鸥之间的碰撞后，海鸥向最佳海鸥的方向移动。

(26)

B=2×A2×rd

(27)

其中rd为[0，1]之间的随机数。

3)保持与最佳海鸥的接近

最后，搜索海鸥可以根据最佳海鸥更新其位置。

(28)

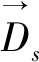
1.2.2 攻击

海鸥在迁移过程中可以不断地改变攻击的角度和速度，它们用翅膀和重量保持高度。当攻击猎物时，在空中发生螺旋式运动行为。在x,y和z平面上的这种行为可描述如下。

x′=r×cos(k)

(29)

y′=r×sin(k)

(30)

z′=r×k

(31)

r=u×ekv

(32)

其中r是螺旋的每一圈的半径，k是一个随机数(0k2π)。u和v是定义螺旋形状的常数，e是自然对数的底。使用公式(29-32)计算搜索海鸥的更新位置。

(33)

SOA从随机生成的总体开始，海鸥可以在迭代过程中根据最佳海鸥更新其位置。将SOA算法主要步骤总结如下表1所示：

表1 SOA算法主要步骤

1.3 改进的BP神经网络预测模型

本文使用SOA算法来优化BP神经网络的参数，提升BP神经网络的预测性能。主要步骤为：

1：初始化参数，Maxiteration=100fc=2，u=1，v=1，海鸥个数n=30，x=1。并将神经网络的权值和阈值编码为初始海鸥种群。

2：初始化海鸥的位置。

4：根据公式(33)更新每一个海鸥的位置。

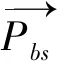
6：将最优的输出解码为BP神经网络的初始权值和阈值，对神经网络进行训练直到满足要求。

2 结果与讨论

2.1 数据预处理

采用青海省某河流中2016年5月-8月采集的数据，每天采集一次，采集指标包括水温(℃)，pH，溶解氧(mg/L)，电导率(us/cm)，浊度(NTU)，高锰酸盐指数(mg/L)以及氨氮(mg/L)，共收集到123组数据，采用前100组数据进行训练网络，后23组数据进行验证网络性能。

由于初始数据的来源多样，类型不同，较难处理，因此，首先必须将数据进行归一化处理，转化到同一参考系下。本文采用改进的方法进行归一化处理，即

yi=(0.8-0.2)×(xi-ximin)/(ximax-ximin)+0.2

(34)

其中xi和yi分别为归一化前后的数据，ximax和ximin分别为归一化前数据的最大值和最小值。在使用样本数据进行训练之前，将缺失或者明显错误的数据进行预处理，降低其对预测结果的影响。

对于缺失数据一般采用线性插值的方法，即取相同条件下的相邻数据来拟合缺失值。即

(35)

其中，xt和xt+j分别为已知t时刻和t+j时刻的水质参数值，xt+i为t+i时刻缺失的水质参数取值。

所有数据经过归一化和剔除异常数据后即可输入神经网络进行训练。

2.2 仿真结果分析

本文BP神经网络采用3层结构，输入层节点数为6，输出层为1，隐含层为6，迭代次数为100。如图3所示是两种算法的收敛比较，

从图中可以看出提出的模型的收敛速度更快，它更快收敛于最优值，收敛精度更高。23组验证数据的仿真结果如图4所示

从图4中可以看出，提出的优化预测模型的预测值更接近实际值，具有比传统BP神经网络预测模型更精确的预测精度。

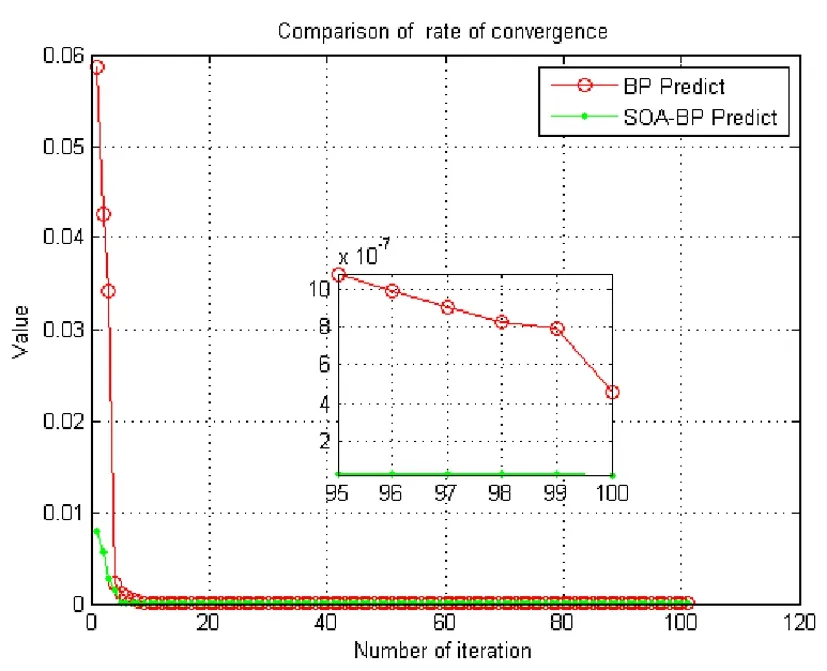
图3 算法收敛比较

图4 预测值与实际值比较

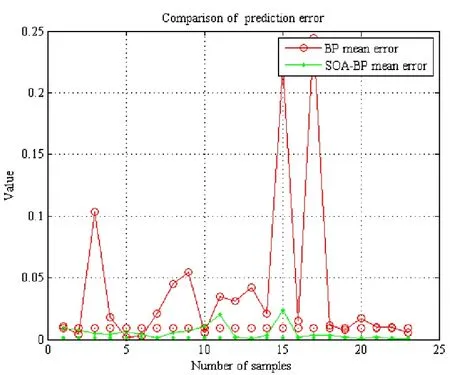
图5 算法预测误差比较

图5为两种算法的误差比较图，取值为误差的绝对值。从图5中可以看出提出的模型对验证样本的误差值更小，平均误差更低，预测精度更高。

对于测试样本进行计算均方根误差(RMSE)比较误差

(36)

其中N为样本数，d(t)为期望输出，y(t)是实际输出，比较值如下表2所示

表2 RMSE值比较

由表中结果显示未优化的BP神经网络预测数据的均方根误差为0.075422，而经SOA优化的BP神经网络的预测数据的均方根误差为0.007996，误差大大减小，优化后的模型预测精度大大提高。

3 结 语

针对传统BP神经网络易限于局部最优和预测氨氮精度较低的问题，本文采用海鸥优化算法对BP神经网络的权值和阈值进行优化，而后得到一种更准确的预测氨氮的预测模型，仿真结果表明该模型的预测精度更高，可适用于更加复杂的水质环境中对氨氮值进行预测。