计算机逻辑回归分析

费云利

（炎黄职业技术学院通识教育中心，江苏 淮安，223400）

1 引言

随着目前机器学习领域和数据挖掘知识的不断进步与发展，该领域中的多项技术被应用在信息网络、营销销售、软硬件操作系统以及生物医疗等众多领域中。顾名思义，数据挖掘主要基本是基于目前的大数据平台，借助机器学习的专业知识与技术对错综复杂以及庞大的各类数据进行快速、高效和高级化处理，并在计算机软件上进行一定的分析与探讨，最终得出相应的结论[1]。在该过程中，不仅要学习和熟悉计算机的编程知识、又要懂得相应概率、线性代数等众多的数学知识，并将其综合应用在实际的业务场景中[2]，由此可见，机器学习以及数据挖掘正以高姿态高标准出现在人们的视野中，并为数据分析师们提供着方便快捷的分析与处理数据的方法。由于目前数据量的增大增多，并且由于数据的复杂度增加，只靠人类大脑是远远不够的，因此基于机器学习的数据挖掘技术被广泛应用[3-4]。主要原理是计算机系统根据已经存在的数据，运用各类数理统计算法进行快速高效分析，并找到其中的规律，建立预测模型，并通过模型对测试集数据进行测试或对预测数据进行结果预 测[5]。本文主要针对某企业客户销售数据对其进行一定的分析与处理，并基于线性逻辑回归、随机森林和XGBoost 三模型进行客户二分类处理，首先对这三个模型进行了理论算法上的介绍与推导，然后基于Python 语言将三类模型应用到实际数据中进行训练和测试，根据预测结论，对三类模型的优劣与不同适用场景进行了探讨。

2 逻辑回归模型Logical Regression

2.1 算法理论

逻辑回归模型本质是一种线性回归模型，但其最大的特点便是在分类输出结果时套用一个特定的逻辑函数Sigmoid，使其能够成为机器学习分类中一个重要的模型[6]，如图1 所示。

图1 Sigmoid 函数

逻辑回归模型（LR）主要被用在二分类问题中，该模型能够将空间的集合映射为一种二分类的可能性（也即概率），即输出变量最终为定性变量{0 或1}。设存在一个二分类问题，输出为y，并且有一个线性回归模型z=wTx+b的输出是一个实数值，而这个实数是无法完成二分类的，这时就需要有一个Sigmoid 函数将z 值转化为{0 或1}，Sigmoid 函数如下所示：

由于Sigmoid 函数的取值范围在0 到1 之间，因此当输入变量x 在之间时，该函数计算的结果都能映射在0 到1 范围内，因此可以认为到目前为止，输出结果是一个二分类概率，可以通过公式（2）定性的变为0 或1。

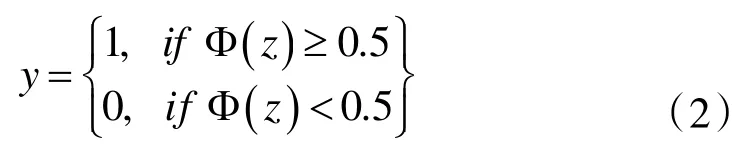
将上述公式（1）代入公式（2）即可得到定性二分类结果。

2.2 逻辑回归模型优缺点

逻辑回归模型是在线性回归的基础上套用一个Sigmoid 函数直接实现的，能够广泛应用在各类工业问题上，并且实现速度快，最适合二分类问题预测[7]。其次对于该模型而言，理论算法中的多重共线性并不是太大问题，因为算法中直接可以利用正则化解决该问题。

该模型的缺点也有很多，例如对大数据量和复杂的场景有限制性的适应能力，不如其他高级算法适应性强。当数据量或变量字段增大到一定程度时，该模型运行性能比较缓慢，影响计算机运行速度。由于模型比较简化，所以在处理比较复杂的问题时，准确度不是很高[8]。目前该算法模型只能处理两分类问题并且需要数据集合线性可分，因此要求自变量和因变量存在一定的线性关系才能使得模型最终效果比较好。

2.3 逻辑回归模型的训练与测试

基于上述理论基础，并利用某公司的营销客户数据，这些数据包含了客户的基础信息（例如年龄、性别、地域等）和行为信息（例如还款信用卡情况、浏览特定网页数量以及购买存款产品的情况等），部分数据如图2 所示。

图2 营销客户数据部分截图

针对营销客户数据，应用逻辑回归模型并基于Python 语言对模型进行训练得到模型对象classifier_LogisticRegression，其中训练集数据占总数据量80%，测试集占总数据量的20%。然后利用classifier_LogisticRegression 对象对测试集数据进行相应的测试，得到最终测试结果，在测试结果中主要利用三种方法来判别模型的好坏，主要包括混淆矩阵、模型准确分和ROC-AUC 曲线。

（1）混淆矩阵

在机器学习的各类模型中，第一个广泛应用于评价模型好坏的指标就是混淆矩阵（Confusion Matrix），通常也被称为错误矩阵[9]。概念如下：

?

根据上述概念，我们构建出二分类经典混淆矩阵，如下所示：

?

上表中TP、TN、FP、FN 代表真实值预测成的数量。由此可得出几个重要性指标：分类模型的准确分：

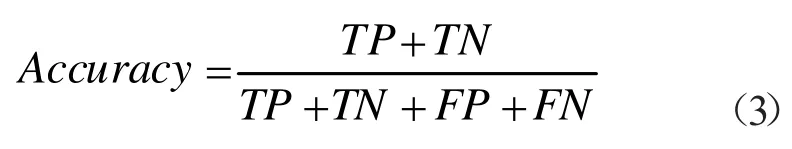
预测为阳值的准确率：

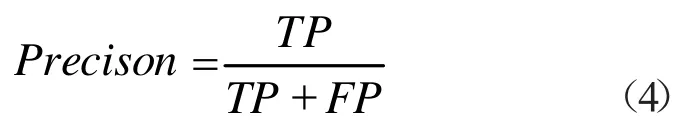
模型敏感度（Sensitivity 或TPR）：

Fall-out 率，也被称为FPR：

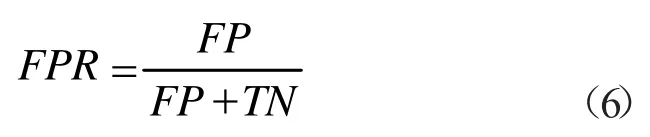
对于多分类（N 分类）问题，相应的混淆矩阵变为N*N 的矩阵。对于混淆矩阵，优点是直观简介，并且二维可见，但其最大的缺点就是有可能存在准确性陷阱（Accuracy Paradox）[10]。

（2）模型准确分

混淆矩阵最大的缺点就是可能存在准确性陷阱（Accuracy Paradox），即如果将所有的真实值简单地预测为某一类，反而会提高模型的准确性。为了解决这个问题，我们引入了模型准确分的概念，模型的准确分混即真实值预测后与原真实值一致的个数除以总样本个数。模型的准确性分数计算方法如下：

（3）ROC-AUC 曲线

首先根据混淆矩阵可以计算出TRP 和FPR，见式（5）和（6）。ROC 曲线是从原点出发，即当原真实值为1，被预测成1，则从原点向上移动一步；而当原真实值为0，被预测成1，则向右移动一步。

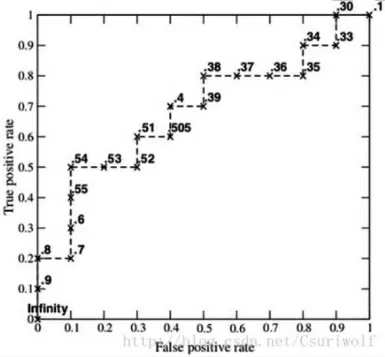
图3 理论ROC-AUC 曲线

当数据量很大时，则图像上则显示出一条递增的平滑曲线，如图4 所示。

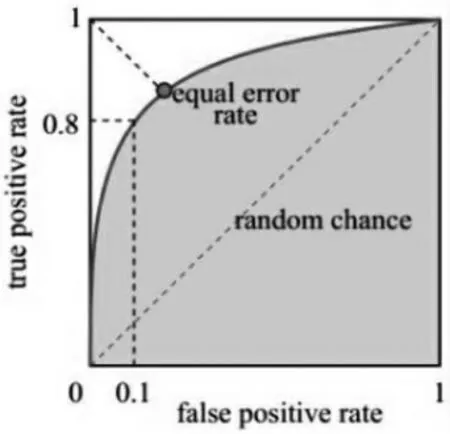
图4 实际ROC-AUC 曲线

ROC 曲线具有很多优点，例如当测试集中的各类样本发生一定分布上的变化时，该曲线能够基本保持不变。因此对于数据集合中正负样本不平衡时，ROC 曲线能够显示出良好的特性。

根据混淆矩阵、模型准确分和ROC-AUC 曲线，应用逻辑回归模型对测试集进行测试，分别得出该模型的三个评判准则的结果：

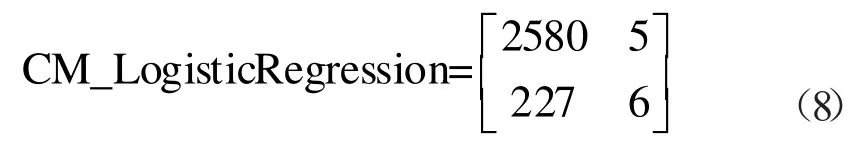
式（8）给出了逻辑回归模型的混淆矩阵结果，从上述结果可以看出，TP=2580，TN=5，FP=227，FN=6，因此从总体结果可以看出模型效果比较好；模型的准确分如式（9）所示：

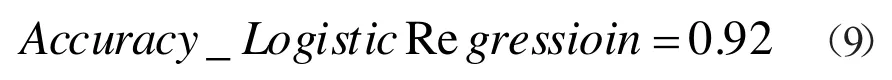
逻辑回归模型的ROC-AUC 曲线如图5 所示：

图5 显示的曲线效果比较好，远大于图中的直线，并且可以计算出曲线与横坐标围城的面积等于0.80018，这个值说明该模型比较好，所以可用于实际数据的二分类[11-12]。

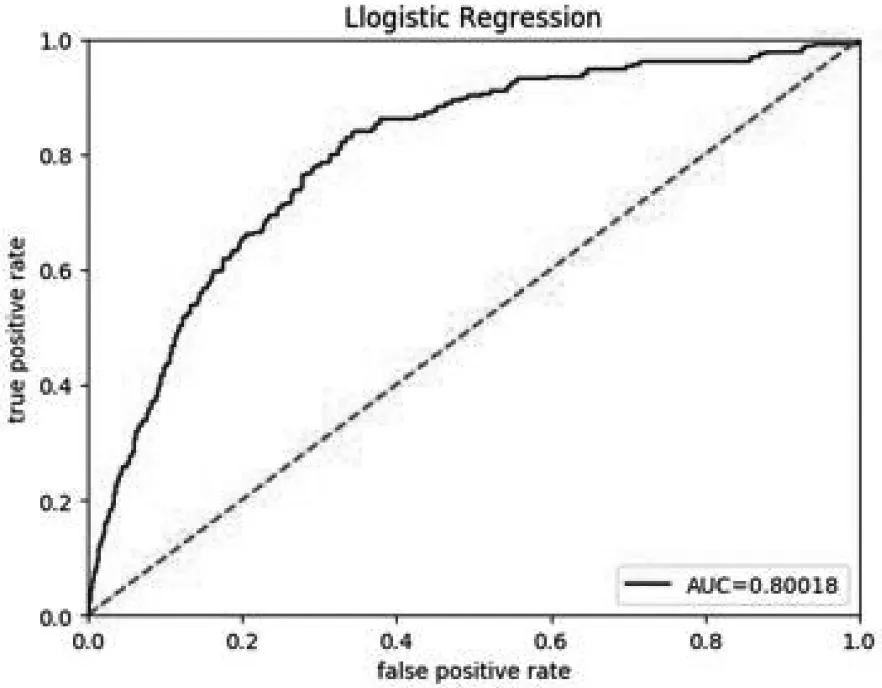
图5 逻辑回归模型ROC-AUC 曲线

3 结语

本文首先探讨了机器学习和数据挖掘在当今社会中各个领域的应用，并对线性逻辑回归模型进行了算法介绍，提出了评价逻辑回归模型的三种方法：混淆矩阵、模型准确分和ROC-AUC 曲线[13-15]。在此基础上上，应用某公司的实际营销客户数据对逻辑回归模型进行了训练，并用测试集数据对该模型进行了有效的测试，得到良好的混淆矩阵，模型准确分等于0.92，以及最后的AUC值等于0.80018，从这三个评判标准可以观察出，模型的效果是比较好的，能够被应用在实际业务当中，为决策者提供有效的帮助。