偏心堆载作用下盾构隧道横断面变形规律及其控制限值

魏纲，洪文强，魏新江，蒋吉清

(1.浙江大学城市学院土木工程系，浙江杭州，310015；2.浙江大学建筑工程学院，浙江杭州，310058)

随着城市轨道交通的发展，运营地铁隧道附近进行堆土、回填的工况越来越多。CJJ/T 202—2013“城市轨道交通结构安全保护技术规范”规定[1]地铁结构的最终绝对位移不能超过20 mm。当地面堆载作用时，地铁隧道衬砌结构会产生附加应力，破坏隧道结构的平衡，引起应力重分布，从而产生一定的变形，尤其是横截面变形。情况严重时会引发隧道管片开裂、螺栓失效和接缝张开等现象，对地铁安全产生严重影响。因此，研究地面堆载对邻近运营地铁隧道的影响具有重要意义。目前，针对此类工程问题，已有部分学者进行了一些研究。研究方法主要为：实测分析[2-6]、理论计算[7-14]、数值模拟[15-22]和模型试验[23-24]。王涛等[10]将隧道结构等效为土层中的弹性地基梁，利用Boussinesq 应力解计算加(卸)载引起的隧道下卧土层中的附加应力，利用Winkler模型计算隧道结构的变形。王如路等[18]采用ABAQUS 软件建立三维有限元模型，研究了地面压载、土体侧向压力系数和土体抗力系数对隧道横向变形发展的影响，还研究了隧道横向变形随压载变化的发展规律，建立了隧道直径变化和混凝土受力、螺栓受力以及接头张开量之间的关系；建立了隧道变形量发展的几何简易分析方法，利用该方法直接测量隧道直径变化就可以判定隧道变形状态。赖浩然等[21]依托苏通GIL综合管廊越江隧道，建立了精细化的三维有限元模型，研究了大面积超载和局部超载作用下衬砌结构的变形和裂损特性，并分析了接缝张开、衬砌变形和结构内力随堆载的发展规律，提出了大面积超载和局部超载作用下，地表超载控制标准。但是人们对常见的偏心堆载工况研究较少，同时，以隧道直径变化作为隧道安全状态评价指标还存在不足之处。在此，本文作者基于修正惯用法，计算盾构隧道衬砌结构在对称堆载和偏心堆载作用下的围压，采用MIDAS/GTS NX软件建立单环管片环的三维有限元模型，分析其在围压作用下的横向变形规律。采用椭圆度作为评价隧道安全状况的评价指标，分析其在偏心堆载工况中的应用情况。

1 盾构隧道围压计算

1.1 地面堆载工况力学模型

运营地铁盾构隧道上方有一偏心矩形的局部堆载，力学计算模型如图1 所示，图中：L和B分别为堆载的长和宽；P为堆载；s为隧道轴线到堆载中心的水平距离；D为隧道的外直径；H为隧道的埋深；Hw为地下水高度。

图1 力学模型的平面和横截面示意图Fig.1 Plans and cross sections of mechanical models

1.2 围压计算方法

取盾构隧道的1个衬砌环进行分析，采用修正惯用法计算衬砌环四周荷载分布[25]，隧道受力示意图如图2所示，图中：P1为水土合算时顶部垂直水土压力；P2为水土合算时底部垂直水土压力；q1为水土合算时顶部水平水土压力；q2为水土合算时底部水平水土压力；K为地层反力系数；δ为衬砌的水平位移；Pp1为堆载引起的隧道顶部远端竖直力；Pp2为堆载引起的隧道顶部近端竖直力；qp1为堆载引起的隧道侧面底部水平力；qp2为堆载引起的隧道侧面顶部水平力；Pg为衬砌底部为平衡垂直方向的自重力而产生的垂直土压力；G为衬砌自重荷载；Re为衬砌形心半径。将衬砌环上的力分解为指向圆心的力和切向力，其中，指向圆心的力即为衬砌环的围压。

图2 隧道受力示意图Fig.2 Stress diagram of tunnel

计算例工况如下：堆载P=100 kPa，L=80 m，B=40 m，堆载中心离隧道轴线水平距离s=20 m，地下水高度Hw=5 m，水的重度为9.8 kN/m3，覆盖土厚度H=10 m，土体重度为18 kN/m3，浮重度为10 kN/m3，土的黏聚力为30 kPa，土的内摩擦角为10°，地层反力系数K=5 MN/m3，侧向土压力系数为0.65，隧道弹性模量E=3.45×107Pa，混凝土密度为2.6 t/m3。

采用文献[26]中的方法计算盾构隧道衬砌结构的围压，计算结果如表1所示，其中，角度对应的是垂直方向围绕隧道横截面中心顺时针旋转该角度后的位置，如90°对应横截面最右端的位置。

2 有限元模型建立

2.1 模型基本假定

假定：1)在管片中，仅对横向管片之间连接的螺栓进行模拟，忽略其他钢筋的影响，将混凝土理想化为各向同性的材料；2)除了管片间螺栓外，忽略橡胶密封垫等其他部件的影响；3)忽略螺栓孔与螺栓之间的空隙，并假设管片与管片、管片与螺栓在开始时均为紧密连接；4)忽略混凝土材料的耐久性性能对混凝土材料本身强度的影响；5)只分析盾构隧道衬砌横向的力学行为，忽略盾构隧道纵向结构变形对横向力学行为的影响。

2.2 管片结构形式

隧道外直径为6.2 m，内直径为5.5 m，衬砌环环宽为1.2 m，管片厚度为0.35 m。管片环由6 块管片组成，采用“1+2+3”的分块方式设计，包含1 块封顶块(圆心角为24°)、2 块邻接块(圆心角为60°)和3 块标准块(圆心角为72°)。管片之间采用2根强度为4.8级的M24螺栓进行连接。

2.3 数值计算模型

采用MIDAS/GTS NX软件建立数值计算模型，如图3 所示。管片环及螺栓均采用边长为0.1 m 的四面体实体单元进行模拟，同时，接触的地方采用界面单元模拟。地层作用在盾构隧道衬砌结构上的抗力通过在衬砌环全周设置法向地基弹簧单元进行模拟，并将地层抗力与盾构隧道衬砌结构位移之间的关系简化为正比关系，其中，比例因子定义为地基抗力系数。

螺栓和混凝土管片的本构模型均采用范梅塞斯模型进行模拟，螺栓2个阶段的弹性模量分别为206 GPa 和70 GPa，转点应力为400 MPa，泊松比为0.3；混凝土重度为25 kN/m3，2个阶段的弹性模量分别为34 988 MPa 和162.8 MPa，转点应力为25.6 MPa，泊松比为0.2[27]。

在模型中将衬砌模型的周边分成24 等份，每份角度为15°，将每部分的围压加上表1 中的垂直均布围压作为盾构隧道衬砌环全周的围压。

表1 荷载P为100 kPa时的围压Table 1 Confining pressure at load P of 100 kPa

图3 衬砌环计算模型示意图Fig.3 Schematic diagram of calculation model of lining ring

3 盾构隧道横断面变形规律分析

3.1 隧道衬砌结构横向变形分析

图4 所示为隧道衬砌结构的位移云图。由图4可知：隧道衬砌结构整体呈现“斜椭圆”变形，椭圆长轴与水平方向成45°左右，与对称堆载情况下的长轴方向为水平方向的横椭圆变形不同。这是因为在偏心堆载作用下，衬砌结构受到竖向和水平方向的压力作用，合力方向与垂直方向呈一定的角度，从而产生斜向“压扁”的效果，混凝土的最大位移为3.5 mm。

3.2 隧道衬砌结构内力分析

图4 隧道衬砌结构位移云图Fig.4 Displacement nephogram of tunnel lining structure

图5和图6所示分别为隧道管片结构和螺栓的平均应力云图。由于隧道结构发生斜椭圆形状的变形，在椭圆长轴两端隧道内侧发生挤压的现象，因而混凝土的应力较大。另外，由于应力集中，在管片与管片的接缝处的应力较大，文献[27]也得到了类似的结果。混凝土和螺栓的最大应力分别为6.4 MPa和21.9 MPa，均发生在邻接块与封顶块的接缝处。

图5 隧道衬砌结构平均应力云图Fig.5 Average stress nephogram of tunnel lining structure

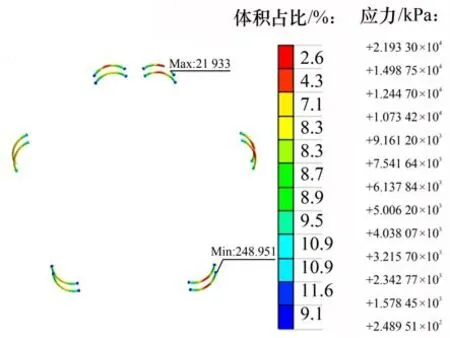
图6 螺栓平均应力云图Fig.6 Mean stress nephogram of bolt

4 横断面变形控制限值

4.1 评价指标的选取

堆载作用下隧道衬砌结构变形示意图如图7所示。从图7可见：在对称堆载作用下，隧道衬砌结构由于受到顶部堆载的作用，从而发生横椭圆变形，变形之后与椭圆形相似，水平直径变长，竖向直径缩短；在偏心堆载的作用下，隧道衬砌结构由于受到斜上方堆载的作用，从而发生“斜椭圆”变形，椭圆的长轴与水平线成一定的角度。

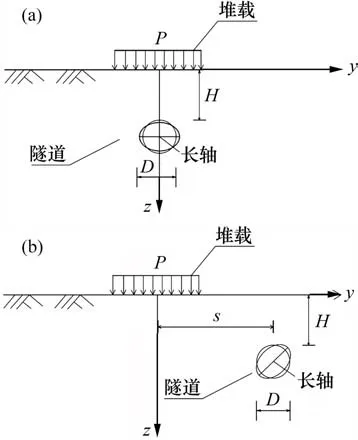
图7 堆载作用下隧道衬砌结构变形示意图Fig.7 Deformation sketch map of tunnel lining structure under surcharge

现有研究大多采用直径变化量为隧道横截面变形的评价指标，仅适用于对称堆载情况，在偏心堆载情况下，由于隧道横截面发生“斜椭圆”变形，将会发生横向直径变化不大甚至没有变化、隧道横截面发生巨大变形的现象。“斜椭圆”变形示意图如图8所示。本文采用椭圆度作为安全评价指标，以非水平方向的长轴变化量和短轴变化量之和除以隧道直径计算得出。

4.2 有限元计算结果分析

4.2.1 对称堆载情况下三维有限元计算

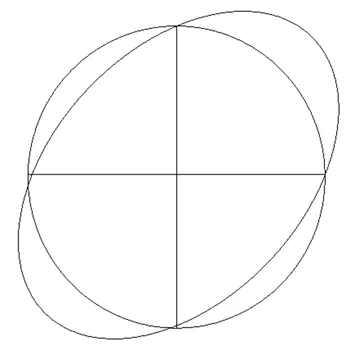
图8 “斜椭圆”变形示意图Fig.8 Oblique ellipse deformation diagram

设计对称堆载工况，在堆载P为100～1 400 kPa(间隔100 kPa取值)，共14种工况下计算隧道的围压，在有限元模型上添加围压并进行模拟计算。

图9所示分别为对称堆载情况下隧道椭圆度与混凝土最大应力、螺栓最大应力之间的关系。由图9 可知：当椭圆度小于等于0.471%时，地面堆载为500 kPa，混凝土应力随着椭圆度增大近似呈线性增加，这是因为随着堆载增加，作用在隧道衬砌结构上的附加应力不断增加，因而隧道的变形增大，椭圆度增大。与文献[22]得到的“水平直径变化越大，混凝土和螺栓最大应力越大”的结果类似。当椭圆度大于0.471%时，混凝土的最大应力为25.6 MPa，这是因为模型中混凝土的本构为非线性本构，此时混凝土已达到最大应力发生破坏。由图9还可知：螺栓最大应力随着隧道椭圆度的增大而增大，其斜率在中间发生变化，当椭圆度大于0.471%时，曲线的斜率变大，这是因为当混凝土发生破坏时，螺栓承受了更大的受力，因而最大应力变大。

图9 对称堆载工况下隧道椭圆度与混凝土和螺栓最大应力的关系Fig.9 Relationship between tunnel ellipticity and the maximum stress of concrete and bolts under symmetrical surcharge

4.2.2 偏心堆载情况下三维有限元计算

设计非对称堆载工况，s=20 m，在P=100～2 700 kPa(间隔200 kPa 取值)这14 种工况下计算隧道的围压，在有限元模型上添加围压并进行模拟计算。

图10 所示分别为偏心堆载情况下，隧道椭圆度与混凝土最大应力、螺栓最大应力之间的关系。由图10可知：当椭圆度小于等于0.326时，地面堆载为1 300 kPa，混凝土应力随着椭圆度的增大近似呈线性增加，与对称堆载情况下(椭圆度为0.471%)相比较小，这是因为偏心堆载情况下，隧道呈现斜椭圆变形，长轴端处于标准块和领接块的接头处，降低了隧道的承受能力。当椭圆度大于0.326%时，混凝土的最大应力为25.6 MPa，这是因为模型中混凝土的本构为非线性本构，此时混凝土已达到最大应力发生破坏。由图10还可知：螺栓最大应力随隧道椭圆度增大而增大，其斜率在中间发生变化，当椭圆度大于0.326%时，曲线的斜率变大，与对称堆载情况下类似。

图10 偏心堆载工况下椭圆度与混凝土及螺栓的最大应力关系Fig.10 Relationship between ellipticity and the maximum stress of concrete and bolts under eccentricloading

4.3 横向变形控制限值

根据文献[28]中的方法计算可得：当堆载为104 kPa时，纵向沉降超过变形限制(20 mm)，对应的堆土高度约为5.7 m，椭圆度为0.005%，混凝土比螺栓先发生破坏；在对称堆载情况下，堆载为500 kPa，对应堆土高度约为27.8 m，椭圆度为0.471%，混凝土发生破坏；当偏心堆载s=20 m，堆载为95 kPa 时，椭圆度为0.007%，对应堆土高度约为5.2 m，纵向沉降超过变形限制(20 mm)，当椭圆度为0.326%时，混凝土发生破坏。

5 结论

1)隧道衬砌结构在偏心堆载作用下整体呈现“斜椭圆”变形，椭圆的长轴与水平方向成45°左右，混凝土的最大位移为3.5 mm。在管片与管片的接缝处的应力较大，应力集中。

2)提出采用椭圆度作为评估堆载情况下安全状态的评价指标，该指标除了适用于对称堆载之外，也适用于偏心堆载作用下的斜椭圆变形。

3)在对称堆载情况下和偏心堆载情况下，混凝土和螺栓最大应力都随着椭圆度增大而增大，近似呈线性增加。当达到混凝土的屈服应力时，混凝土发生破坏，最大应力不变；此时，螺栓承受了更大的受力，因此，螺栓最大应力增长较快，螺栓最大应力-椭圆度曲线斜率变大。

4)本文采用Boussinesq法计算偏心堆载对隧道产生的附加应力，而修正惯用法适用于均质土层，对于非均质土层可以进行进一步研究；同时，以1个环管片环为研究对象，忽略了管片环与管片环之间的相互作用力，无法研究通缝与错缝之间的差别，建议可以以3～4个环管片环作为研究对象进行进一步研究。