基于动态辊缝的连轧机多参数耦合颤振建模及工程应用

2020-05-18王桥医张秋波王瀚崔明超

中南大学学报（自然科学版） 2020年3期

王桥医，张秋波，王瀚，崔明超

(杭州电子科技大学机械工程学院，浙江杭州，310018)

轧机颤振[1-3]是连轧薄板高速轧制过程中出现的最具破坏性的振动问题，它突然发生，通常在几秒内达到最大振幅，这种振动会导致轧制板带间非常明显的厚度波动和张力波动[4-5]，甚至会导致板带断裂，还会加速支承辊的磨损，造成支承辊的不定期更换，从而增长了设备维护的成本。考虑到连轧机颤振对生产产量、产品质量和维护成本的影响，连轧机颤振不仅是现代轧制生产中需要面对的技术问题，也是制约轧制生产成本的经济问题[6-8]。近年来，人们一直在研究轧制过程中的颤振问题，但由于轧制过程本身的复杂性，研究仍然不够深入。在现有的轧制模型[9]中，有些模型过于简单，无法精确地捕捉轧制过程的特征，而有些模型则过于复杂，无法得到精确的解析解。HU 等[10]提出轧机的第三倍频颤振现象，建立了一种结合均匀轧制过程模型和轧机结构模型的轧机颤振模型，并对系统的稳定性进行分析，确定了轧制工艺参数对稳定性的影响，得到了系统的稳定性判据。ZHANG 等[11]通过对前滑比的分析指出，带钢在颤振过程中其入口速度是变化的，而出口速度是恒定的，提出了轧机振动类型为由于带钢张力与工作辊垂向振动之间存在相位延迟而产生的自激振动，BRUSA 等[12]通过对轧机轧制生产过程的观察发现，轧机发生颤振时机架间张力变化较大，机架间张力的变化是引起垂直轧制力变化的主要因素，从而引起轧辊组的垂直振动。PENG等[13]发现：在各工艺参数中，张力设置、摩擦因数和轧制速度对系统稳定性起重要作用。HEIDARI等[14-15]认为：存在最佳摩擦条件使轧制速度达到最大值，基于两机架自激振动模型，提出了各机架的稳定性判据。候福祥等[16]总结了轧机自激振动产生的原因及其研究现状，归纳了轧机振动的控制措施，指出目前研究存在的问题，并从多个方面对轧机振动的研究提出了展望。闫晓强[17]以连轧机为研究对象，通过振动遥测系统得到其振动测试信号，确定其振动的性质为机电液耦合振动，通过扭振抑制器，优化自动厚度控制参数的方法有效地抑制了连轧机的耦合振动。郜志英等[18]总结了轧机颤振的研究现状，主要包括轧机结构模型、垂直和扭转振动模型以及耦合振动模型，考虑非线性因素和非对称性因素的振动问题，以及基于Slab 分析方法的轧制过程模型和仿真分析等。本文基于均匀变形理论并考虑轧件加工硬化效应和轧辊弹性压扁效应建立了轧机动态轧制过程模型，然后将该模型与轧机机架结构模型耦合建立了以状态空间表示的轧机单机架颤振模型，再以单机架颤振模型为基础，结合机架间的张力耦合和轧件厚度波动在机架间存在的时滞传递效应，建立了连轧机颤振模型。

1 考虑动态辊缝轧制过程模型

1.1 动态辊缝的几何特征

轧制过程辊缝的基本几何特征如图1所示，坐标系的原点是当轧辊静止时，上下工作辊中心的垂直线与轧件中心线的交点，图中：w为轧件宽度；h1和h2分别为轧件入口和出口厚度；u1和u2分别为轧件的入口和出口速度；σ1和σ2分别为轧件入口和出口处张力；R'为变形后工作辊半径；vr为工作辊圆周速度。轧件运动方向与x轴正方向相反，假设上下工作辊关于x轴的振动情况是对称的，在静态轧制过程中，轧件出口平面与其中心线重合，但在动态轧制过程中，工作辊在y轴方向上以hc/2的速率振动，其中，hc为沿辊中心线的辊缝间距。

图1 辊缝几何特征Fig.1 Roll bite geometry

1.2 轧件加工硬化效应

金属内部晶粒的再结晶会使塑性变形增加，从而导致金属屈服强度增加，一般情况下，可通过实验数据拟合得到应力-应变曲线来描述轧件加工硬化效应。应力-应变之间的关系可以用多种公式表达，其中，应用较为广泛的动态轧制过程应力-应变公式如下：

式中：Kf为考虑加工硬化的轧件变形抗力；σ0，A，n为通过实验确定的材料参数；ε为有效屈服形变，

h0为轧件初始厚度；h为轧件厚度。

式(1)和式(2)仅适用于平面应变，其中，A和n应取轧件发生加工硬化效应前的参数。

在连轧机组中，轧件在上一个机架出口处的流动应力与其在下一个机架入口处的流动应力相同，但从一个机架到下一个机架的应变累积会导致流动应力的增加，也就是说，下游机架的流动应力一般比上游机架的大。

1.3 轧辊弹性压扁效应

工作辊和轧件间的轧制力会导致工作辊发生弹性形变，忽略工作辊弹性压扁效应会减小辊缝内工作辊和轧件间的接触长度，从而导致轧制力计算时产生偏差，因此需要建立一种考虑工作辊弹性压扁的数学模型。

一般假设辊缝内压力分布为椭圆形，则变形后的轧辊形状仍为圆形，工作辊的有效半径为

式中：R为轧辊原始半径；E为弹性模量；γ为工作辊的泊松比；f为单位轧件宽度的轧制力；r为压下量。

为了简化轧制过程的分析，假设沿工作辊与带钢的接触弧的工作辊有效半径在总轧制力发生变化时仍然保持不变，则在静态轧制过程中可以用工作辊的有效半径代替其初始半径进行计算。另外，在轧辊组的结构模型中，可将工作辊视为刚性弹簧，当施加的轧制力发生变化时，除了工作辊会发生位移外，轧件厚度也会发生变化，通过上述假设可明显提高轧制过程动力学模型的精度。

1.4 动态辊缝轧制应力分布

辊缝处轧制力切块法分析如图2所示。采用切块法分析辊缝内压力分布可得：

式中：μ为摩擦因数，对于轧件出口区域，使用上侧的负号，而对于轧件入口区域，使用下侧的正号；p为主应力；σx为辊缝内的压力，则轧件屈服准则的表达式变为

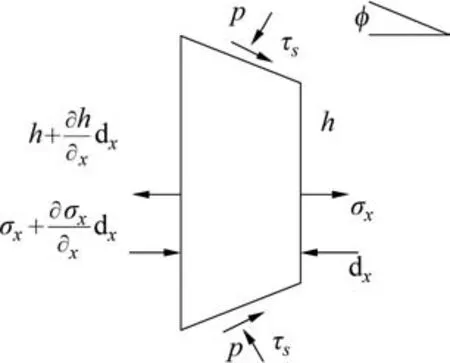
图2 辊缝处轧制力切块法分析Fig.2 Slab analysis on a volume element of roll gap

将式(5)代入式(4)可得：

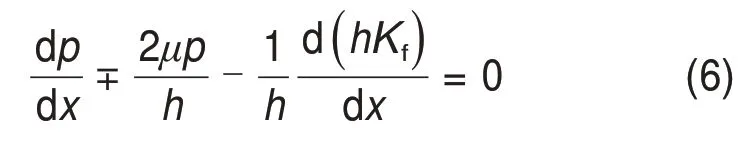
求解式(6)可以得到动态辊缝轧制压力分布，但这种方法的计算比较复杂，因此可建立一个近似的压力分布表达式来代替式(6)进行求解。由于轧件从入口区到出口区的过程中厚度h会减小，变形抗力Kf会增加，因此可假设接触弧处的h和Kf的乘积为常数，式(6)中的第3项就可以忽略，可得：

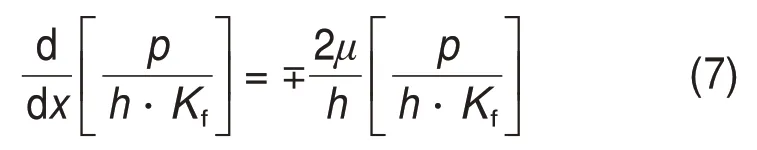
式(7)的边界条件为：

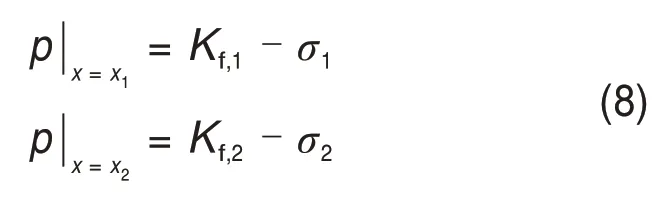
式中，Kf,1和Kf,2分别为轧件入口处x=x1和出口处x=x2的变形抗力；入口侧和出口侧的轧制力p-和p+分别为：

式中：H1和H2分别为轧件入口处和出口处的H；

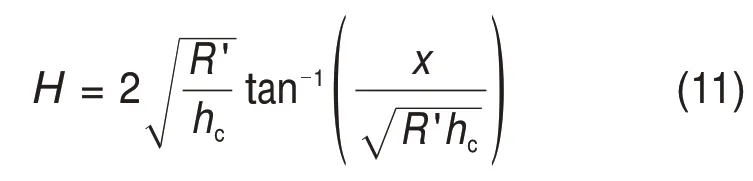
式(9)和式(10)说明轧制力取决于入口、出口和中性点的位置、材料的加工硬化特性以及入口及出口张力。

1.5 轧制力和轧制力矩

已知动态轧制过程中入口、出口和中性点的位置，沿辊缝内接触弧对式(9)和式(10)积分可得到轧制力和轧制力矩。由于入口处和出口处的轧制力表达式不同，因此必须分别从入口处到中性点进行积分和从出口处到中性点进行积分，则单位宽度的轧制力可表示为

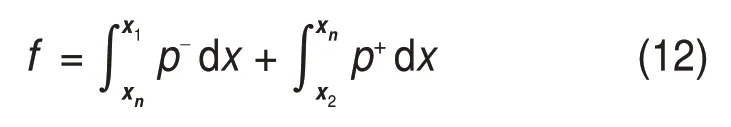
将式(9)和式(10)代入式(12)可得：

通过对摩擦力积分可以计算出轧制力矩，上工作辊摩擦力示意图如图3所示。摩擦力的方向在中性点处发生改变，因此对摩擦力要分成2部分进行积分，则单位宽度的轧制力矩可表示为

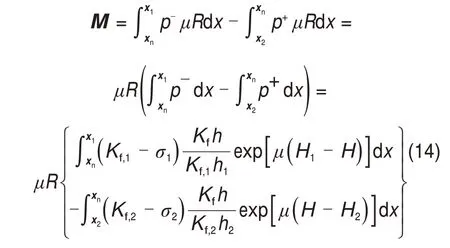
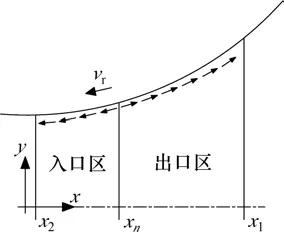
图3 上工作辊摩擦力示意图Fig.3 Friction acting of the top work roll

2 连轧机颤振模型的建立

2.1 四辊轧机五自由度结构模型

四辊轧机研究中常用的简化模型中较为经典的有单自由度模型以及四自由度模型等，本文考虑了轧制力的非线性因素以及机架的质量和刚度，建立了四辊轧机五自由度结构模型，如图4 所示。四辊轧机可简化为五自由度垂直系统，它由5个质量元件组成，其中：M1和M4分别为下支承辊系和上支承辊系的等效质量；M2和M3分别为下工作辊系和上工作辊系的等效质量；M5为机架的等效质量；y1～y5为M1～M5各等效质量元件对应的垂直振动位移；K1为下支承辊系和机架的等效刚度，K2为下工作辊系和下支承辊系的接触刚度；K3为上工作辊系和上支承辊系的接触刚度；K4为上支承辊系与机架的等效刚度；K5为机架的等效刚度。假设轧机系统仅在垂直方向上发生颤振，采用弹簧常数KR表示轧制力变化时工作辊和轧件间的弹性变形抗力，由于辊缝与轧制力之间的非线性关系，采用dfy来表示轧制力的变化量。

图4 四辊轧机五自由度模型Fig.4 Model of a four-high mill(five degrees of freedom)

由图4 可知：当作用在轧辊上的力发生变化时，轧辊之间的位移也会发生变化，轧辊位移与轧制力波动量dfy之间的关系可用一组二阶微分方程表示：

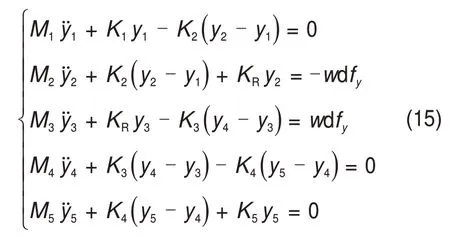
该模型可用于在连轧机的时域动态响应仿真研究。

2.2 连轧机相邻机架间的耦合关系

机架间的关系如图5所示。在连轧机组中相邻机架有2种重要的耦合关系，分别为轧件张力耦合和轧件厚度在机架间波动耦合，根据胡克定律，机架i入口处的应力变化与机架i-1 出口速度和机架i入口速度之差的积分成正比，即：

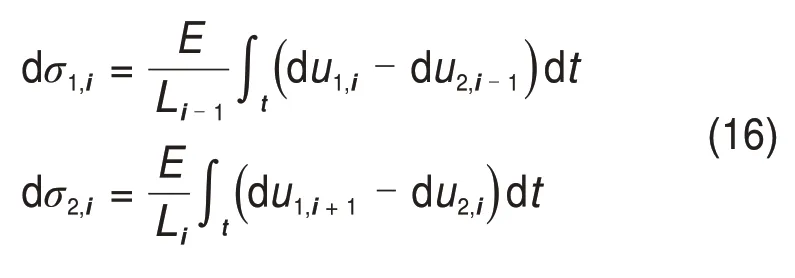
式中：Li-1为机架i和机架i-1之间的距离。

式(16)也可表示为

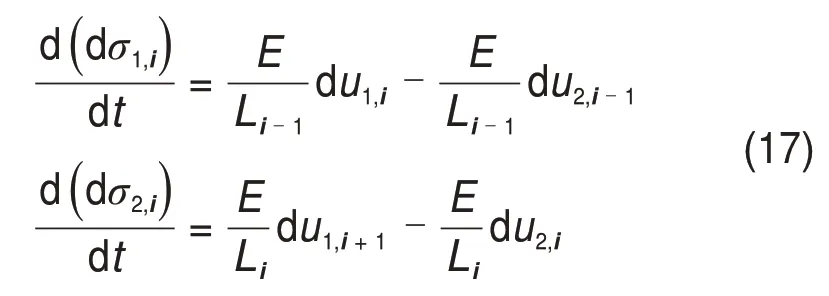
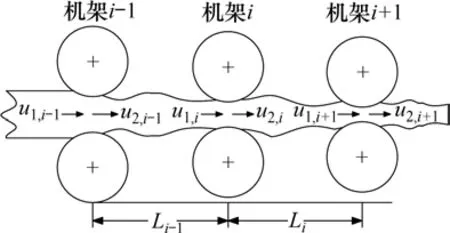
图5 机架间的关系Fig.5 Relationship between mill stands

前一个机架轧件厚度的变化对下一个机架的影响是再生效应研究的重要方面，机架i入口处和机架i-1 出口处轧件厚度变化关系的传递函数表示为

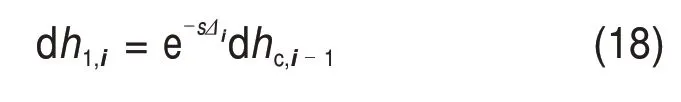
式中：s为拉普拉斯变量；Δi为机架间的时间延迟，

2.3 单机架颤振模型

单机架颤振模型如图6所示。将轧制过程模型与轧机结构模型相耦合，考虑机架之间的相互作用，可以建立单机架的轧机颤振模型，为了考虑机架间的张力耦合，该模型还加入了开卷机和卷取机，假定开卷机和卷取机工作速度恒定，即式(16)中开卷机的出口速度du2,i-1和卷取机入口速度du1,i+1不发生变化，则位于该开卷机和卷取机之间的机架间张力变化纯粹是由机架本身的入口和出口速度变化产生的，可以采用状态变量(dhc，dḣc，dσ1，dσ2)来描述，该系统的输入量是入口处轧件厚度变化量dh1。

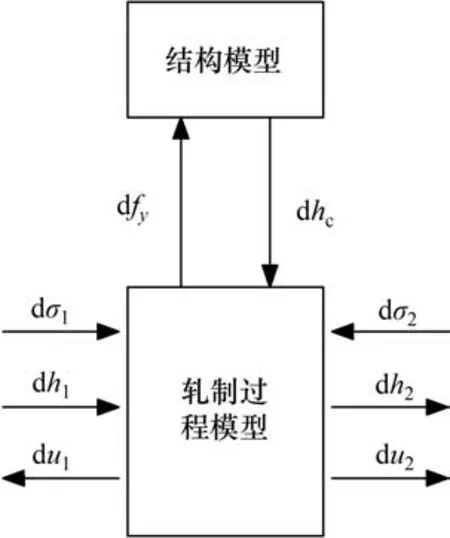
图6 单机架颤振模型Fig.6 Single stand chatter model

则单机架颤振模型可用一组一阶微分方程矩阵形式表示为

式中：C为阻尼系数；Fi，Pi和Qi分别为动态轧制模型的系数；i= 1,2,3,4,5；wF2为轧件在辊缝内发生塑性变形产生的正阻尼；为张力变化产生的负阻尼；wF1为辊缝内轧件的接触刚度，该参数会导致机架固有频率的增加。

基于上述颤振模型，可对单机架的负阻尼效应进行研究。

2.4 多机架颤振模型

在连轧机轧制过程的最后阶段，经常会出现颤振现象，为研究机架间行为对系统整体稳定性的影响，基于已提出的单机架颤振模型，建立了适用于多机架颤振分析的动力学模型，如图7所示。

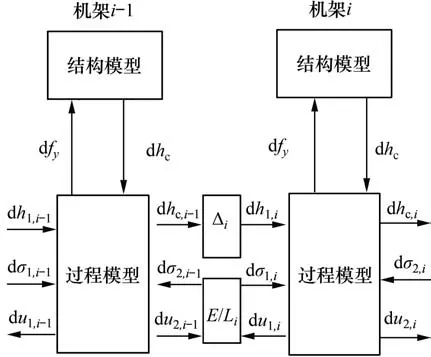
图7 多机架连轧机颤振模型Fig.7 Chatter model for a multi-stand tandem mill

机架间张力变化可通过式(17)计算。多机架颤振模型由2 个机架组成，每个机架有4 个状态变量，因此，动态模型共有8个状态变量，但是，机架i-1 的前张力变化等于机架i的后张力变化，则系统的独立的状态变量为7个，并令：

则两机架结构的状态空间矩阵表示形式为

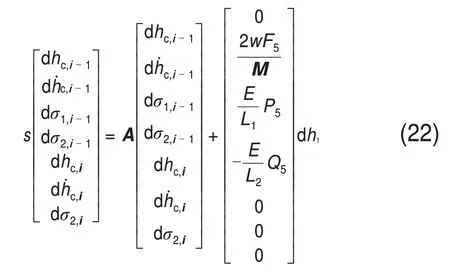
式中：A=

式(22)是时滞微分方程，需要通过较为复杂的稳定性准则来进行稳定性分析。式(22)第1 列中的时间延迟量Δ在再生效应的研究中极为重要，若忽略时滞项，则该模型也可用于研究多机架负阻尼机理。

用同样的方法建立由2个以上机架组成的连轧机的状态空间模型。在多机架颤振模型中，每增加1个机架，系统的状态变量就会增加3个。

3 连轧机系统颤振模型仿真计算及分析

连轧机组通常有2个以上的机架，典型的连轧机组包括5～6个机架，由于轧件在连轧机多机架间具有时滞传递效应，这使得连轧机系统的稳定性分析相当困难，因此，可采用仿真分析来研究连轧机系统的稳定性。

以某企业五机架冷连轧机为例，对连轧机多机架颤振模型进行验证。表1所示为连轧机轧制工艺条件，由于五机架冷连轧机各机架结构类似，因此各机架的结构参数设置相同，M1=M4=53 000 kg，M2=M3=7 700 kg，M5=70 000 kg，K1=K4=15.5 MN/mm，K2=K3=46.3 MN/mm，K5=32.3 MN/mm，R′=700 mm，w=900 mm，L=4.5 m。

图8 所示为五自由度结构模型在轧制速度vr=18 m/s时各机架的时域响应图。

从图8可知：各机架辊缝变化量较小，且机架3、机架4、机架5的振动持续时间较长，这表明五自由度系统需要较长的时间来减弱振动，轧件振动从机架1 到机架5 的传递时间约为4.2 s，机架5在此处的辊缝变化量最大，这说明轧件厚度的传递在振动传播过程中非常重要。

当轧制速度vr增大到25 m/s时各机架的时域响应如图9所示。从图9可见：五自由度结构模型变得更加不稳定，机架4 和机架5 的振动呈指数增长；与机架4 和机架5 相比，机架3 的辊缝变化量较小，这表明3号机架的振动是由4号机架的振动引起的。

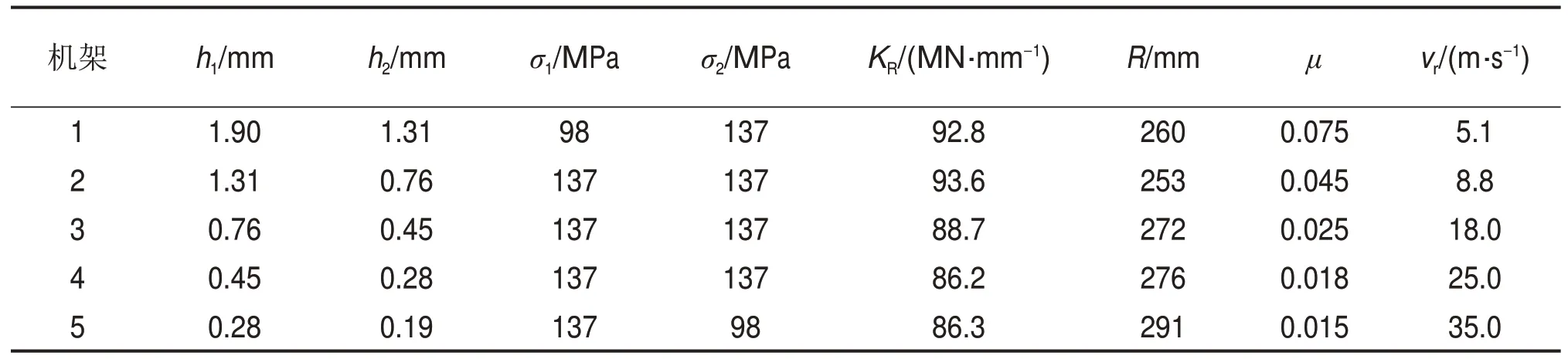
表1 连轧机轧制工艺条件Table 1 Conditions of the rolling process in a tandem mill

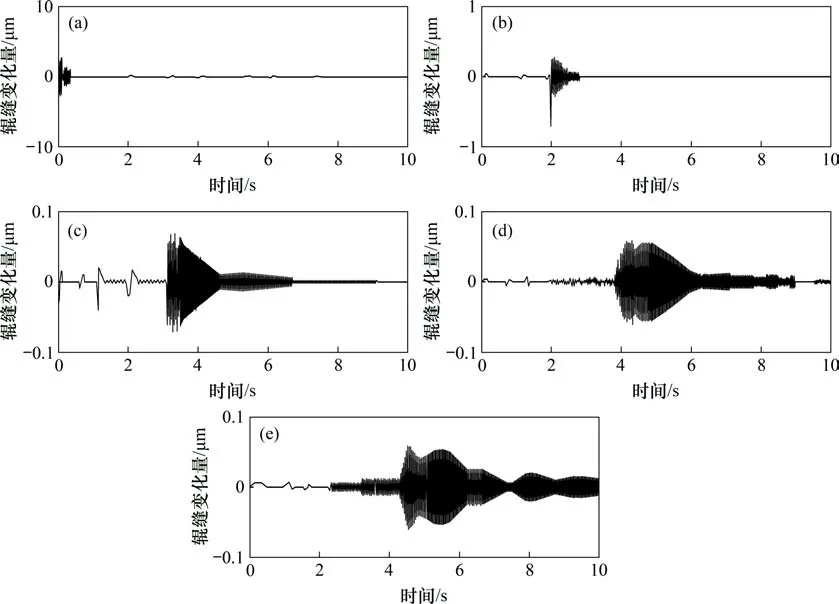
图8 vr=18 m/s，μ=0.025时各机架的时域响应Fig.8 Time domain response of stand when vr=18 m/s，μ=0.025

图10 所示为五自由度机架结构中5 个质量元件的位移。从图10 可以看出：工作辊的位移比支承辊和机架的位移小得多，且轧件上工作辊系和上支承辊系的振动趋势类似，下工作辊系和下支承辊系的振动趋势也类似，但上下工作辊的振动位移相差较大，下工作辊位移比上工作辊的小，这是因为上部机架不是非常刚性稳定造成的。

五自由度结构模型中没有阻尼项，这是多质量元件的机架结构需要较长的时间来减弱振动的原因，在当前机架的振动完全消除之前，轧件厚度波动在一段时间延迟后从上一个机架进入当前机架，这种情况会进一步放大当前机架的振动，最终导致整个轧制系统的不稳定。

图9 vr=25 m/s，μ=0.018时各机架的时域响应Fig.9 Time domain response of stand when vr=25 m/s，μ=0.018

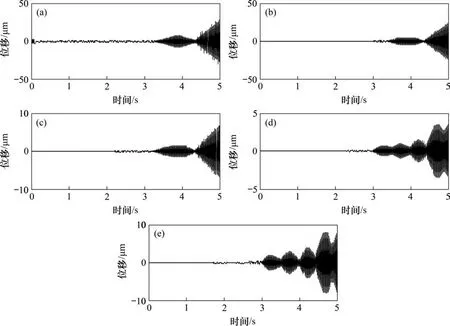
图10 五自由度结构轧辊位移Fig.10 Roll displacements of five-degree of freedom structure

通过仿真研究了轧机系统在时域上的动态特性，轧件在机架间传递的时滞效应会显著降低系统的整体稳定性，颤振包括2个重要的因素，即机架间张力耦合和轧件传递的时间延迟效应，时间延迟效应是影响机架之间耦合最重要的因素，任何不考虑时间延迟效应的稳定性分析都会导致连轧机系统稳定性分析的错误。虽然单个机架是稳定的，但是由于机架间的再生效应连轧机整体也可能会失稳。在单机架系统中，可以用张力波动引起的负阻尼效应来验证系统的稳定性，但在连轧机中，必须考虑轧件的时滞传递效应，因为轧件厚度波动的传递是将各独立的机架耦合成整体轧制系统最为关键的因素。