考虑驱动摩擦效应的冗余并联机构动力学建模
2020-05-18卢超秦伟胡小亮唐小斌刘飞谢志江
卢超,秦伟,胡小亮,唐小斌,刘飞,谢志江
(重庆大学机械传动国家重点实验室,重庆,400044)
在某大型高超声速喷管段中,需要设计一种重载三自由度调整机构来调整其中的型面段,从而实现对喷管型面位姿进行精确控制[1-3]。冗余驱动并联机构可以提高机构的承载能力与控制精度,获得较好的刚度特性及动态性能[4-6]。并联机构的动力学可以通过拉格朗日法、牛顿-欧拉法、虚功原理等方法进行分析[7-13]。这些方法各有优缺点,拉格朗日法和虚功原理适用于理想约束下的动力学模型求解,即不考虑摩擦效应;当需要考虑摩擦效应时,牛顿-欧拉方法是建立动力学模型的有效方法,但求解过程比较复杂。山显雷等[14]基于牛顿-欧拉法建立了考虑关节摩擦的3SPS+1PS 并联机构显式动力学,对比了理论计算与实际测量的驱动力,对并联机构的动力学控制及摩擦补偿提供了理论依据;王庚祥等[15]利用牛顿-欧拉法建立了考虑“库仑+黏性”摩擦效应的动力学模型,结果表明,当并联机构处于初始阶段和高速运动时其关节摩擦力对该机构驱动力的影响较为明显;李研彪等[16]在考虑关节摩擦效应的情况下,采用牛顿-欧拉法建立了5-PSS/UPU并联机构的动力学模型,并进行动力学耦合特性分析;SHANG等[17-18]在工作空间内建立了动力学模型,并提出新的动力学和摩擦自适应补偿方法,该自适应方法能够实时评估动力学和摩擦参数,从而实现自适应动态补偿和摩擦补偿。基于此,本文作者设计一种平面3自由度4-PRR冗余并联机构,并建立考虑驱动副摩擦的动力学模型,采用范数最小原则对滑块驱动力进行优化求解,并提出结合虚功原理和牛顿-欧拉法2 种方法建立动力学模型,由最小范数解得到驱动力。将考虑驱动副“库仑+黏性”摩擦效应得到的驱动力与不考虑摩擦效应的驱动力进行对比,得到驱动副摩擦效应对机构的动力学性能影响规律,为此类机构的动态控制与摩擦补偿奠定基础。
1 机构模型描述与运动学逆解
1.1 机构模型描述
喷管段实际应用结构如图1所示,主要由型面动平台、基座及连接2个平台的运动支链构成。机构共有4组8条运动支链,每条分支包含相同的运动部件和运动副,每条支链由1个滑块导轨移动副P 和2 个转动副R 组成,移动副P 为驱动副。为防止运动过程中滑块相互干涉,将滑块分别置于不同的导轨上,即8个滑块在4条导轨上运动。
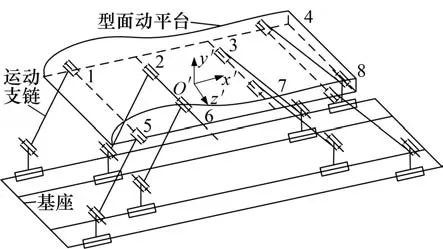
图1 8-PRR并联机构结构简图Fig.1 Schematic diagram of 8-PRR parallel mechanism
由于并联机构为1R2T三自由度机构,且关于x′O′y′平面对称,为便于分析,将机构简化为如图2所示的平面4-PRR冗余驱动并联机构。
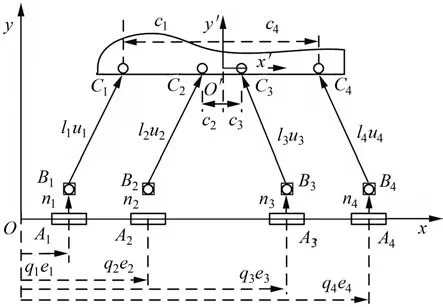
图2 4-PRR并联机构结构简图Fig.2 Schematic diagram of 4-PRR parallel mechanism
在风洞坐标系原点建立定坐标系xOy,在动平台质心O′建立动坐标系x′O′y′。其中,qi为各移动副中心Ai至y轴的距离,li为拉杆长度,ei为移动副的单位方向矢量,ni为铰链点Bi到移动副轴线的距离矢量,ui为拉杆的单位方向矢量,ci为铰链点Ci到动坐标系原点的距离矢量,i=1,2,3,4,C1和C2在x′轴的负方向,C3和C4在x′轴的正方向。第i条支链的封闭矢量图如3所示。
由图2和图3可知:动平台的位姿可由位置矢量r和旋转矩阵oRo′描述。动平台绕定坐标系旋转角为θ,则位置矢量r和动坐标系相对于定坐标系的旋转矩阵oRo′分别为

图3 PRR支链i封闭矢量图Fig.3 Vector diagram of the i th PRR kinematic chain

1.2 运动学逆解
对该冗余并联机构的运动学进行求解,包括位置逆解、滑块速度与加速度、拉杆速度与加速度。
1.2.1 位置逆解
采用封闭矢量解法求运动学逆解,建立位置封闭矢量方程:
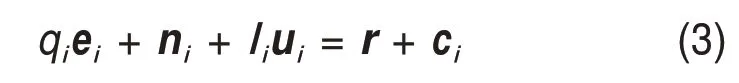
并联机构的逆解模型为
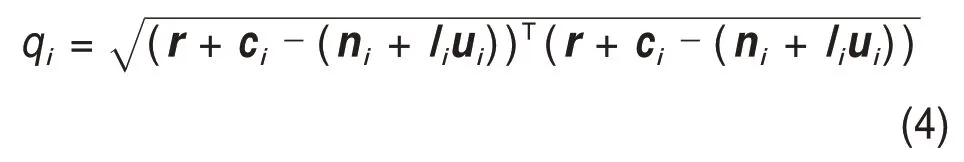
由并联机构的结构形式及该机构的结构参数即可得到4条支链驱动滑块的位置逆解表达式。
1.2.2 滑块速度分析
并联机构有3个自由度,包括沿x,y方向的平动和绕垂直于xoy平面的转动,令动平台速度和加速度分别为:

式中:v和w分别为动平台线速度和角速度;v̇和ẇ分别为动平台线加速度和角加速度。
将式(3)两侧对时间求导可得:

将式(7)两侧点乘ui并简化可得:

式中:vCi为铰链点Ci的速度;wi为拉杆i在定坐标系下的角速度;为支链i的雅可比矩阵。

1.2.3 拉杆速度分析
将式(7)两侧点乘,并将式(8)代入可得到拉杆的角速度表达式:

由式(7),拉杆的质心速度为

式中:E为单位矩阵;Jiv和Jiw分别为拉杆的线速度雅克比矩阵和转动角速度雅克比矩阵。
结合式(10)和式(11)得到拉杆质心的线速度以及拉杆的转动角速度:

其中:Jivw为拉杆的速度雅可比矩阵。
1.2.4 滑块加速度分析
将式(7)两侧对时间求导得

式(13)两侧同时点乘ui并简化得

则滑块加速度为

1.2.5 拉杆角加速度分析
式(13)两侧同时点乘Eˆui可得:

则拉杆角加速度为

1.2.6 拉杆质心加速度分析
将式(11)对时间求导并简化得

则拉杆质心加速度为
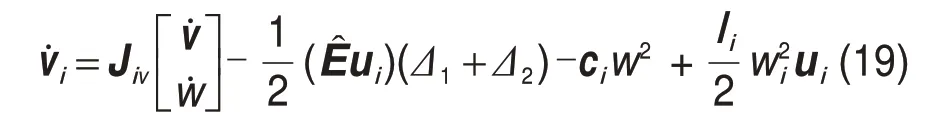
2 机构动力学求解
2.1 无摩擦动力学求解
当不考虑机构驱动摩擦效应时,根据机构质量及其所受外力得到机构的动力学模型如图4 所示,图中,mqi为滑块i的质量;mli为拉杆i的质量;mP为动平台的质量;ne为动平台外力矩;fe为动平台外力。
动力学建模方法主要包括牛顿-欧拉法、凯恩法、拉格朗日功能平衡法以及虚功原理法。当不考虑摩擦力时,虚功原理建模方法在执行效率和算法上效果更好。本文首先采用虚功原理来建立不考虑摩擦力的冗余并联机构动力学模型。
对于动平台,外力、惯性力和重力合力为

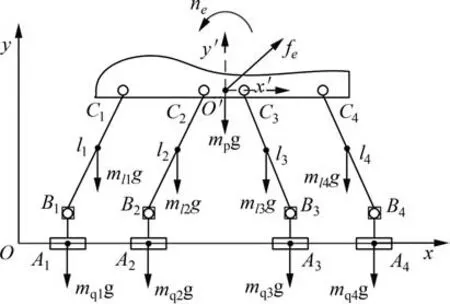
图4 4-PRR并联机构动力学模型Fig.4 Dynamic model of the 4-PRR parallel manipulator
式中:g为重力加速度;oIp为动平台在定坐标系下的转动惯量。
对于支链i的拉杆,重力为所受唯一外力,则惯性力和重力合力为

式中:oIli为拉杆在定坐标系下的转动惯量。
对支链i的滑块,只有平动,则作用在滑块上的驱动力、惯性力和重力合力为

即滑块驱动力fq=f+K,驱动关节驱动力f=[f1,…,f4]T,K=[K1,…,K4]T。
由式(20)~(22),虚功原理可描述为

式中:δxp为动平台的虚位移,δxp=[δxpδypδθp]T;δxi为拉杆i的虚位移,δxi=[δxi δyi δθi]T;δq为滑块驱动虚位移;N为导轨对滑块的反作用力。
虚位移δxp,δxi与δq满足机构关节的约束,其关系为

将式(24),(25)代入式(23)可得:

式(26)对任意的δxP均成立,因此有

式中:-A为机构受到的力。
本文的冗余驱动并联机构具有3个自由度,对应4 个驱动力输入,J为非方阵,在任何运动状态下,驱动力在理论上都存在无穷多组解,根据范数最小原则可求得其解,

式中:(JT)+=J(JTJ)-1,为矩阵JT的广义逆矩阵,对于冗余并联机构,范数最小解驱动力一般为最优驱动力解。
2.2 考虑驱动副摩擦动力学建模
摩擦是一种复杂的非线性物理现象,产生于具有相对运动的接触界面之间,很难从机理上获得其准确唯一的数学模型,只能利用复杂的数学模型无限地接近摩擦的真实现象。为简化其仿真过程,采用参数辨识容易、模型结构简单且适用范围相对广泛的摩擦模型“库仑+黏性”摩擦模型,如图5所示。

式中:v为滑块与基座的相对滑动速度;fv为黏性摩擦因数;fc为库仑摩擦因数。

图5 “库仑+黏性”摩擦模型Fig.5 “Coulomb+viscous”friction model
基于建立的无驱动摩擦动力学模型,引入驱动关节摩擦的作用建立动力学模型。对该并联机构的单个支链进行受力分析如图6所示,图中,fPli为动平台作用于运动支链i的力矢量;fqili为滑块作用于运动支链i的拉杆的力矢量;Ni为基座作用于运动支链i的滑块的y向力矢量。
在对支链i进行受力分析的基础上,对滑块、拉杆进行受力分解,如图7 所示,图中,fqilix和fqiliy为fqili在滑块i上沿x和y方向的力矢量;fPlix和fPliy分别为fPli在拉杆i上沿x和y方向的力矢量;Ni1和Ni2为fqilix对考虑长度的滑块i产生的力矩效应与滑块所受正压力的合力矢量。

图6 PRR支链受力分析Fig.6 Force analysis of PRR chain

图7 PRR支链i受力分解Fig.7 Force decomposition of the i th PRR chain
由运动学分析可知滑块和拉杆的运动状态在给定动平台运动规律下已知。由图(7)所示受力分解,当不考虑摩擦力时,fqilix由对滑块在x向采用牛顿方法得到

拉杆的运动状态只受滑块和动平台的力的影响,当拉杆运动状态已知时,对拉杆采用牛顿欧拉方法得
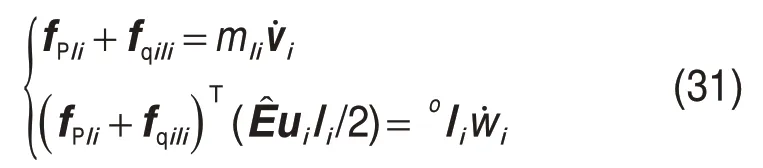
式(31)含有4 个未知数3 个方程,不论是否考虑摩擦力,fqilix大小、方向都不变。结合式(30)推导出fqili,故可求得拉杆对滑块的全部作用力。
已知拉杆对滑块的全部作用力,由式(29)可求得支链i上的摩擦力为

式中:Ni为正压力,Ni= |mqi g+(-fqili)+kAR|Mqi||+|mqi g+(-fqili)-kLR|Mqi||,kAR为滑块径向方向力矩等价系数,kLR为滑块反径向方向力矩等价系数,Mqi为拉杆对滑块相对于基座产生的力矩,

由式(28)和式(29),当考虑摩擦力时,利用驱动力补偿摩擦力F(v)i得到支链i上实际驱动力Fi为
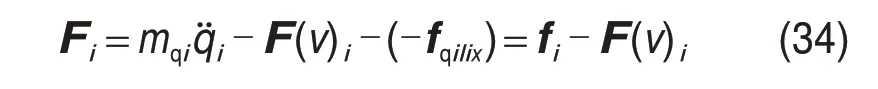
即考虑驱动摩擦效应时滑块实际所需驱动力F=[F1F2F3F4]T。
3 数值模拟分析
综合分析该风洞试验条件及并联机构的实际要求,并联机构的参数如表1所示。

表1 并联机构结构参数Table 1 Geometrical parameters of parallel manipulator
作用于动平台的外力=[-128.5 -1765.6]TN;=103.2 N·m,则在定坐标系中外力为

根据滑块导轨选型手册取kAR=7.56×10-2,kLR=4.86×10-2;根据机构使用环境,“库仑+黏性”摩擦模型中fc=0.15,fv=0.05。
根据并联机构在风洞中的状况,选择余弦函数轨迹进行刚体动力学分析,其运动轨迹如下:

式中:t为时间。
利用Matlab 编程进行数值计算,由式(9)和式(15)得到滑块的速度与加速度曲线如图8 和图9所示。

图8 滑块速度曲线Fig.8 Velocity curves of sliders
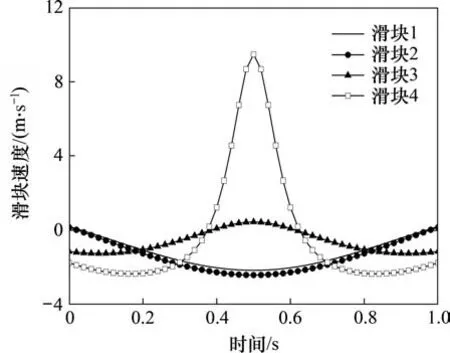
图9 滑块加速度曲线Fig.9 Acceleration curves of sliders
由式(28)和式(33)得到滑块的驱动力曲线如图10所示。
由图10(a)可知:当t=0.50 s时,在考虑摩擦效应状况下,滑块1驱动力发生突变。当t<0.50 s时,滑块1 速度沿x正方向,摩擦力沿x负方向,滑块驱动力沿x正方向,摩擦力和驱动力反向成为阻力,故t<0.50 s时,考虑摩擦效应的滑块驱动力大于不考虑摩擦效应的滑块驱动力;反之,当t>0.50 s时,考虑摩擦效应的滑块驱动力小于不考虑摩擦效应的滑块驱动力。

图10 滑块驱动力Fig.10 Driving force of sliders
由图10(b)可知:不论是否考虑摩擦效应,滑块2 的驱动力规律都与滑块1 的相同,滑块1 与滑块2的驱动力变化比较明显。
由图10(c)可知:当t=0.32,0.50 和0.68 s 时,在考虑摩擦效应状况下,滑块3 驱动力发生突变。当0 由图10(d)可知:当t=0.50 s时,在考虑摩擦效应状况下,滑块4 驱动力发生突变。当0 因此,当考虑驱动副“库仑+黏性”摩擦效应时,滑块驱动力会因摩擦力的变化而变化,摩擦力既可以作为有利力而减小实际驱动力,也可作为阻力而增大实际驱动力。因所选择的模拟轨迹和摩擦模型不同具体的摩擦影响不同。 1)建立了4-PRR 冗余并联机构的运动学逆解模型,根据坐标变换和结构特点得到运动学逆解和机构的雅可比矩阵,得到构件的加速度模型,为动力学分析提供了基础。 2)利用虚功原理构建了机构不考虑“库仑+黏性”摩擦效应的动力学模型,得到范数最小解的滑块驱动力。然后结合牛顿-欧拉方法建立了考虑驱动副“库仑+黏性”摩擦效应的动力学模型。 3)给定动平台运动规律,利用MATLAB 仿真得到各个滑块的速度、加速度变化规律以及考虑驱动副“库仑+黏性”摩擦效应与否的滑块驱动力变化规律,并对速度、驱动力的变化规律进行了分析,驱动副摩擦效应对实际驱动力有显著的影响。 4)冗余并联机构运动学和考虑驱动副“库仑+黏性”摩擦效应动力学模型建立方法可作为解决此类机构的一般方法,对驱动副摩擦严重或者进行摩擦补偿有一定的实际应用意义。4 结论
