用于列车定位的RAIM算法改进研究

赵 妍,米根锁

(兰州交通大学自动化与电气工程学院,兰州 730070)

引言

在实际列车运行过程中，导航系统中存在故障卫星会使可见卫星数目不足或卫星结构分布不良，从而导致车载接收机到卫星之间的伪距值出现偏差，进而计算的列车实际位置结果不准确威胁行车安全[1，2]。因此，针对如何及时检测识别故障卫星进行研究显得十分重要。RAIM(Receiver Autonomous Integrity Monitoring，接收机自体完好性监控)算法是接收机内部通过接收机自身多余观测值，对卫星的多个导航解进行一致性检验，从而达到监测列车定位完好性的目的[3-4]，以保证列车的安全运行。

目前，RAIM算法逐步在铁路领域展开研究。文献[5]对RAIM算法在铁路领域的可用性做出判断，但未对故障卫星的检测与识别做出研究；文献[6]提出用传统RAIM算法计算的检验阈值，但直接检验的漏警率较大。文献[7]提出一种基于扩展卡尔曼滤波器的RAIM算法，新算法性能增益无明显提高，但为后续EKF-RAIM算法的研究奠定了基础。文献[8]设计了一种双递归粒子滤波器的RAIM算法用于分离定位和速度估计，但对铁路领域未进行验证。文献[9]提出加权最小二乘法，针对北斗/GPS组合导航系统的电离层、对流层干扰因子进行研究。

针对上述问题，根据我国自主研发的北斗卫星导航系统运用到列车定位中的特殊形式，提出以ATPL(沿股道方向保护级别，Along Track Protect Level)为判据的RAIM算法，同时，在故障卫星识别环节引入加权因子C。以青藏铁路某路段实际运行数据为例进行仿真验证，证明改进算法的有效性。

1 北斗导航列车定位原理

北斗卫星导航定位系统通过测量出已知位置的卫星到车载接收机之间的距离(伪距)，综合多颗可见卫星的数据，根据三曲面相交确定动态点计算车载接收机的位置信息[10-12]。北斗卫星导航系统定位框图如图1所示。

图1 北斗导航系统定位框图

2 基于ATPL的RAIM算法

2.1 基于ATPL算法的RAIM可用性判断

2.1.1 使用参数

(1)可见卫星判断

在实际工程中，卫星的高度角h>15°(卫星遮蔽角)时，表明该卫星为可见卫星[13]。可见卫星判别如图2所示。

图2 可见卫星判别

(2)完好性水平告警限值

文献[14]指出完好性水平告警限值(HAL，Horizontal Alert Limit)是RAIM算法可用性重要影响因素之一，RAIM算法可用性要求卫星保护级别必须小于告警限值，保护级别越低表明算法使用的可靠性越高。见表1。

表1 不同线路HAL值及可用性

2.1.2 RAIM算法可用性判断

RAIM算法可用是故障卫星检测和识别的前提，图3为RAIM可用性判断流程。

图3 RAIM可用性判断流程

在铁路领域，列车沿固定方向，在固定路线上行驶(一维坐标)，进而直接定义ATPL作为RAIM算法是否可用的判据，在计算ATPL过程中加入列车质心速度方向与钢轨的夹角(航向角)，对传统RAIM算法进行改进。

根据读取的广播星历计算得出，当可见卫星数>4时，表明可以进行RAIM算法可用性判断；当可见卫星数目>5时，表明RAIM算法可以检测到故障卫星，同时可将故障卫星排除。

ATPL的计算

ATPL=KAT×dAT

(1)

(2)

(3)

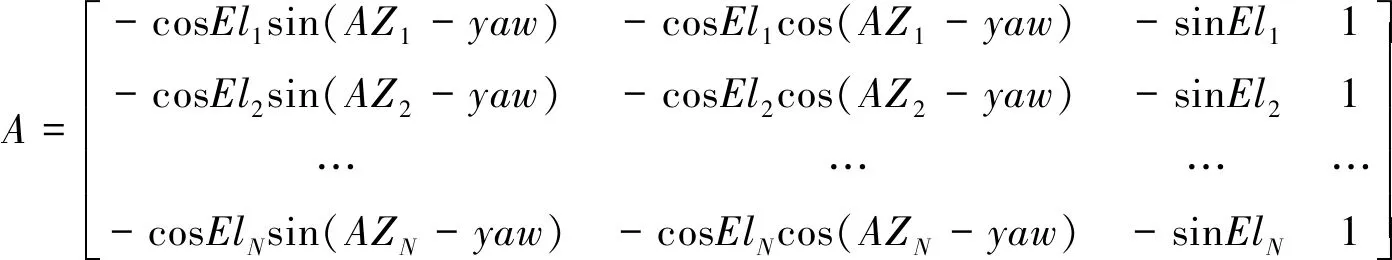
(4)

其中，KAT指一维高斯分布情况下的常数6；σi指第i颗卫星伪距测量误差的标准差；H为加入导航角后的N×4的观测阵；yaw指东北天坐标系下列车航向角；AZi指每个卫星方位角；Eli指每个卫星高度角。

将计算的ATPL与HAL进行比较，判断RAIM算法是否适用。当ATPL>HAL时，说明RAIM算法可用，可进行下一步故障卫星的检测与识别。

2.2 最小二乘残差法故障卫星检测识别

2.2.1 使用参数

(1)故障检测参数

RAIM的技术性能由系统的完好性参数决定，航空无线电委员会(RACA，Radio Technical Commission for Aeronautics)指出完好性参数有漏警率PMD、误警率PFA、告警时间TTA[15-18]。

PMD是指已出现故障卫星，而RAIM技术没有检测出故障卫星的概率。

PFA是全球卫星导航系统(GNSS，Global Navigation Satellite System)在未超出所设定限制的情况下，采用RAIM算法进行检测发出告警的概率。北斗卫星导航系统的最大误警率为0.333×10-6。

TTA是指从发现卫星故障到做出报警的时间间隔。一般导航系统告警时间为6 s。

(2)位置精度因子

位置精度因子(PDOP，Position Dilution of Precision)是可以反映用户所在位置误差与卫星所在位置误差关系，且准确度较高的定位结果计算的PDOP值越小[19]。

(3)故障卫星分类

接收机自主完好性检测的故障模式主要包括以下3种。

①卫星信号发播异常，如信号失锁，信噪比降低。

②故障卫星被提前告知为“不健康”卫星，这主要由导航电文提供。

③发生软故障导致伪距产生偏差。

2.2.2 最小二乘残差法故障卫星检测

当可见卫星数大于5个时，采用RAIM算法对故障卫星进行检测和识别，图4为RAIM算法故障卫星检测与识别流程。

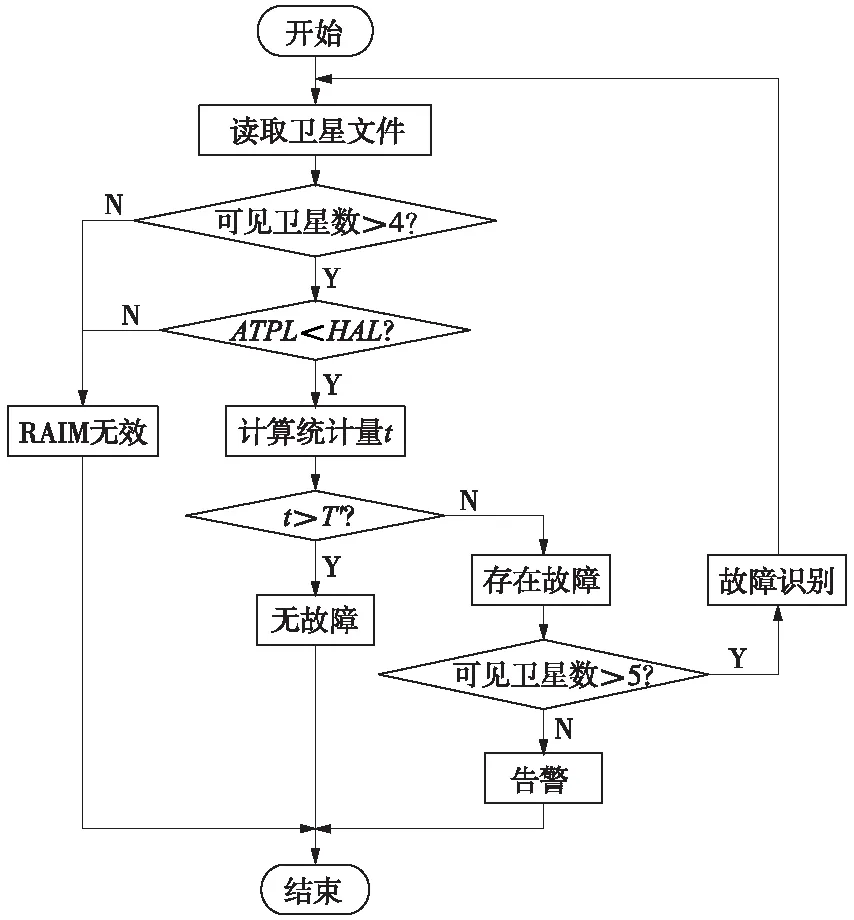
图4 故障卫星检测识别流程

(1)北斗卫星导航系统观测模型

根据北斗卫星导航系统检测原理，线性化后的在东北天坐标下的接收机伪距观测方程为

y=Ax+ε

(5)

其中，y指伪距观测和近似计算伪距差分向量，维数n，y∈RN，N指可见卫星数；A为由卫星到接收机的方向余弦构成的观测矩阵，A∈RN×4；ε指测量误差向量，ε∈RN，ε的每个元素分量在卫星无故障时是均值为零的高斯白噪声。

由最小二乘法可得x的最小二乘估值

(6)

伪距残差向量

(I-A(ATA)-1AT)(Ax+ε)=

(I-A(ATA)-1AT)ε

(7)

令Q=I-A(ATA)-1AT则(3)式可化简为

v=Qε

(8)

基于残差平方和的故障检测

SSE=vTv

(9)

式中，SSE指卫星伪距残差向量平方和。

H0(无故障)：E(ε)=0，则SSE/σ2～χ2(n-4)；H1(有故障)：E(ε)≠0，则SSE/σ2～χ2(n-4，λ)。

PFA(误警率)计算公式

(10)

已知PMD(漏警率)的情况下，当存在故障卫星时，且SSE/σ2～χ2(n-4，λ)，λ的计算公式

(11)

当可见卫星结构分布不良时，故障卫星会对列车定位结果产生较大的误差，同时，会产生漏检率。而通过上述算法计算出的t，会有较大漏警发生，为保证RAIM算法在检测故障卫星时漏检率的要求，对检测阈值引入加权因子C，则有T′=CT，0T′时，说明有故障卫星存在。

2.2.3 基于残差元素的故障卫星识别

当检测到存在故障卫星后，通过最小残差二乘法和极大似然估计法进行故障卫星的识别。当被测噪声满足正态分布且期望值为零时，用公式(12)识别故障

(12)

式中：v(i)指第i号卫星的伪距残差向量；Q(i，i)指Q矩阵第i行第i列元素。

利用公式(12)计算出每颗卫星的λ值，其中故障卫星的λ值最大。

PDOP值的计算

H=(ATA)-1

(13)

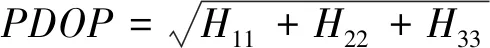
(14)

式中，Hii指H矩阵第i行第i列元素。

3 仿真验证

3.1 RAIM算法可用性验证

(1)RAIM算法可用性验证

根据中国卫星导航系统管理办公室测试评估研究中心数据可知，亚太地区可见卫星数一般为7～14颗。文献[20]指出青藏铁路属于低密度线路，保护级别为50m。

目前常用以HPL(Horizontal Protect Level)法为判据来判断RAIM算法的可用性，通过改变判据改进RAIM算法。本次验证选取青藏铁路同一路段运行轨迹数据，设置检测时间720 min，对改进前后RAIM算法可用性进行验证。图5是在相同运行轨迹情况下改进前后保护级别对应的保护级别曲线，其中HPL值的波动范围为11.2～22.6 m，ATPL值的波动范围为6.1～11.6 m，由于ATPL仅为沿股道方向的保护限值，在同一时间点，ATPL值始终小于HPL值，且在低密度线路保护级别阈值内。经过改进，明显使该路段的保护值降低，也说明RAIM算法可用。

图5 青藏铁路某段路线ATPL、HPL曲线对比

(2)加权因子C对RAIM算法的影响

当RAIM算法可用时，根据某型号接收机的误警率PFA=1/15 000，漏警率PMD=0.001，完好性告警限值HAL=556 m，计算不同C对PFA、PMD及RAIM算法的可用性的影响。见表2。

表2 不同C对RAIM可用性及完好性的影响

图7 各卫星λ计算值

根据表2可知，通过引入加权因子C，使PFA及PMD的值有效降低，达到提高RAIM算法可靠性的目的，且在提高可靠性的同时，不影响RAIM算法的有效性。

3.2 RAIM算法故障检测识别验证

当RAIM算法可用时，进一步检测故障卫星和识别故障卫星。由于缺少北斗卫星导航系统在铁路列车定位应用时的故障数据，因此，结合3.1节数据通过MATLAB仿真软件对RAIM算法的故障检测识别功能进行验证。

本次验证过程中选取9颗符合列车运行地区的无故障可见卫星，设定检验阈值T=4时，设定检测时间为300 s。对检测中的10号卫星的第65 s增加90 m的伪距值，制造故障卫星。

对10号卫星增加伪距值后，通过改进的RAIM算法验证故障卫星是否存在。从图6可知，检测过程的第65 s处卫星的检测量远大于检验阈值T，说明在第65 s处有故障卫星存在。

图6 故障卫星检测

通过式(12)计算每颗卫星的λ值，曲线如图7所示图。根据图7可得10号卫星的λ值最大，符合制造的故障卫星。因此说明以ATPL为参量的RAIM算法可以识别北斗卫星导航系统中的故障卫星。

通过式(13)式(14)计算得到剔除故障卫星前后的列车运行PDOP曲线(图8)。根据图8可得，剔除故障卫星后的PDOP始终小于剔除故障卫星前。通过改进的RAIM算法剔除故障卫星，可以有效降低故障卫星对定位结果PDOP的影响，从而改善卫星故障场景下的定位精度。

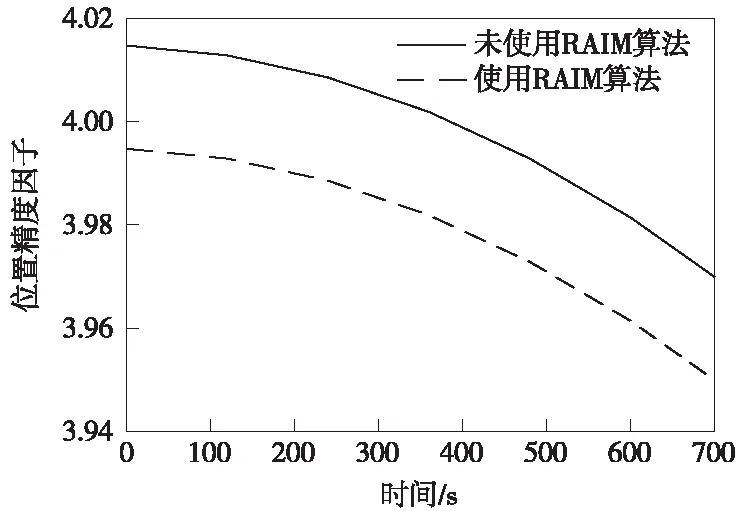
图8 PDOP变化曲线

5 结论

从提高北斗卫星导航系统列车定位精度和降低漏警率的角度出发，提出了一种改进的RAIM算法。在定位过程中，通过改变RAIM算法判据及检测阈值，使得保护值及漏警率有效降低，在不影响RAIM算法可用性的同时达到提高可靠性的目的。通过采用青藏铁路实际列车定位数据进行仿真验证，结果表明改进的RAIM算法优于传统RAIM算法，可准确识别故障卫星，降低漏警，减少故障卫星对PDOP影响，能改善列车定位精度，提高北斗卫星用于列车定位的安全可靠性。