基于多时域特征量的轨道不平顺状态综合评估

杨翠平,王 平

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031； 2.西南交通大学土木工程学院,成都 610031)

准确评估轨道的平顺状态及恶化程度，是保障轨道安全性、平顺性和稳定性的基本前提，对铁路工务养护维修具有重要意义[1-2]。目前，现行轨道评价方法能否满足平顺性要求成为研究重点。文献[3-5]对不平顺管理标准进行研究，分析表明我国现有不平顺管理标准的严格程度和单元区段长度选取为200 m均合理。文献[6-8]介绍了我国现行轨道不平顺动态管理方法，分析了轨道几何管理和均值管理的相关性和现有的轨道不平顺评价管理方法的特征以及局限性。文献[9]建议补充完善与幅值评价对应波长的轨道质量指数验收标准。文献[10]基于多体动力学理论和综合检测列车实测数据，探讨300～350 km/h高速铁路轨道长波高低不平顺管理标准和评价方法建议。文献[11-12]建立了30 t轴重重载车辆-轨道空间耦合模型，研究不同轨道几何不平顺条件下的列车动力性能，提出不平顺管理幅值建议。文献[13-18]探讨轨道不平顺波长对高速行车动力性能的影响，得到各速度等级下轨道静态几何尺寸容许偏差管理值，并提出敏感波长范围取值建议及提取敏感波长的方法。

现有的研究工作已从多个层面完成对轨道不平顺评价方法合理性的探讨。对比发现，这些研究工作最终几乎全部基于同一个评价指标，即轨道质量指数(TQI)。在对轨道状态的监测中发现，现有的管理办法仍存在很多不足，如轨道局部波动不能被有效识别，且存在潜在轨道病害被遗漏的现象。寻找到更合理的评估方法，实现轨道状态科学准确的监测，避免轨道的欠维修或者过维修造成的经济损失，仍具有重要意义。基于此，提出利用轨检车对线路的定期检查所采集的大量检测数据，进行数据挖掘，统计其多个时域特征量并进行主成分分析进行降维处理，选取多个能基本覆盖原始不平顺数据所包含信息的特征量，结合现有的管理指标TQI对轨道平顺状态进行综合评估。此方法可以最大化利用现有的大量不平顺原始数据，放大被TQI指标所忽略的信息，对轨道可能存在的病害进行预警，对铁路工务部门经济合理地安排轨道养护维修计划具有重要意义。

1 时域特征量

时域特征量是衡量信号特征的重要指标，时域特征值通常分为有量纲参数与无量纲参数。在信号表征时，有量纲指标虽然对信号特征比较敏感，但也会因工作条件的变化而变化，并极易受环境干扰的影响，具有表现不够稳定的缺陷。相比而言，无量纲指标能够排除这些扰动因素的影响，因而被广泛应用于特征提取的领域当中。

现有轨道状态评估的主要方法是利用轨检车检测轨道所采集的数据来分析轨道病害，同时这也是世界上其他国家检测轨道病害的主要方法，评估方法主要包括峰值扣分法和轨道质量指数(TQI)法。该方法对数据本身的挖掘程度不够，能反映的信息量比较单一而且不够稳定，不能充分利用轨检车测得的大量数据对轨道实际状态进行准确地评估。为了弥补此缺陷，采用多个主要能反映轨道不平顺幅值概率密度函数特征的时域特征量，避免根据TQI对轨道实际运行状态判断的结果失准，根据概率统计的置信度实现多个特征量的自适应。此方法适用于简易诊断、快速评价轨道状态优劣，可以为铁路工务部门科学有效地监测轨道状态提供有效的信息，对合理制定养护维修计划提供指导。

由于轨道伤损及复杂的运营条件，导致轨道不平顺的实际分布状况偏离理想状态下的标准正态分布，一般情况下认为，若偏离程度越大，则轨道状态越复杂，其存在病害的可能越高。基于此，选取多个能反映轨道不平顺分布规律的特征量，对随机量的分布情况进行多角度的观察，以观测其与理想状态下正态分布的差异。除去现有的轨道质量指数，目前常用的时域特征量的意义与计算方法见文献[19]，分别选取平均值、标准差、峰值、峰值因子、均方根值、绝对平均值、偏度、偏度因子、峰度、峭度、峭度因子、脉冲因子、能量、能量矩、Sharon熵，并对特征量分别排序为1～15。某些特征量所能反映的信息有所重合，本节不做赘述，关键特征量及其物理信息在下文探讨时做进一步说明。

2 特征参数降维处理

2.1 主成分分析法(PCA)

将各个时域特征量作为能反映原始数据信息的变量，多个特征变量虽然可以为数据的挖掘和应用提供丰富的信息，但是在一定程度上，过多的变量大大增加了数据分析的工作量，同时大多情况下，各个变量之间可能存在较强的相关性，从而增加了问题分析的复杂性，但盲目减少指标会造成有用的信息丢失，对问题的有效分析带来不利的影响甚至得到错误的结论。因此，在减少需要分析的指标同时，也要尽量减少原指标包含信息的损失，以达到对所收集数据充分利用与全面分析的目的，避免造成数据浪费。主成分分析(Principal components analysis，以下简称PCA)就属于这类降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

2.1.1 PCA的基本原理

假定有N个样本，每个样本有P个变量，构成一个N×P阶的数据矩阵

(1)

当变量P较多时，在P维空间分析问题比较困难繁琐，由于各变量之间存在不同程度的相关性，因此将多个关系紧密的变量变成尽可能少的相互独立的新变量，那么就可以用较少的综合指标尽量多地反映原始数据所包含的信息。

定义：记x1，x2，…，xp为原变量指标，z1，z2，…，zm(m≤p)为新变量指标

(2)

其中，zi与zj(i≠j;i，j=1，2，…，m)相互无关；zi是x1，x2，…，xp的一切线性组合中方差最大者；zm是与z1，z2，…，zm-1都不相关的x1，x2，…，xp的所有线性组合中方差最大者。则新变量指标z1，z2，…，zm分别称为原变量指标x1，x2，…，xp的第一，第二，…，第m主成分。主成分分析的实质就是确定原来变量xj(j=1，2，…，p)在诸主成分zi(i=1，2，…，m)上的载荷lij(i=1，2，…，m;j=1，2，…，p)。从数学上可以证明，载荷lij分别是相关矩阵的m个较大的特征值所对应的特征项向量。

2.1.2 各主成分的计算步骤

(1)计算相关系数矩阵

(3)

rij(i，j=1，2，…，p)为原变量xi与xj的相关系数，rij=rji，其计算公式为

(4)

(2)计算特征值与特征向量

①解特征方程|λI-R=0，求出特征值，并使其按大小顺序排列

λ1≥λ2≥…≥λp≥0

(3)计算主成分贡献率及累计贡献率

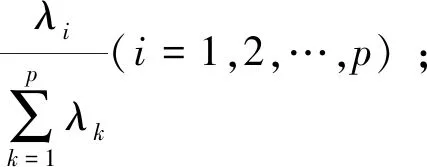
一般取累计贡献率达85%～95%的特征值λ1，λ2，…，λm所对应的第1、第2…第m(m≤p)个主成分。

2.2 降维处理实例

轨道不平顺数据样本选取某高速铁路K600+000～K610+000区段2015年4月9日GJ型轨道检查车检测数据，以200 m为一个单元长度，计算所有单元的15项特征量作为变量，构成50×15阶的数据矩阵，见表1。

表1 各区段轨道不平顺15项统计指标

观察表1可知，不同区段的同一指标差异或大或小，可以理解为不同指标将数据所包含的信息进行了不同程度的放大以及丰富，也证明了用多指标评估不平顺的合理性。将表1的数据作标准差标准化处理，然后将他们代入前文的计算步骤，最终得出各主成分的特征向量即各主成分在15个统计指标的载荷分布情况，以主成分Z1为例，见表2。

表2 主成分Z1的各特征量载荷

由表2可知，各主成分与其中的某些指标有较大的载荷系数，可以认为该成分与该指标有较强的正相关或者负相关，即这些指标可以较强地反映出原始数据所包含的较多信息。综合考虑贡献率较大的前4个主成分的各指标的载荷大小，以及这些指标所代表的实际意义，最终确定选择现有的TQI指数即标准差、峰度、偏度、峭度因子、能量、sharon熵等6个评价指标对轨道的平顺状态进行综合评估。

3 不平顺综合评估实例分析

3.1 潜在病害区段定位

以某高速铁路K677+000～K730+000区段2016年7月27日的实测左高低不平顺数据为例，采用本文方法对线路平顺性进行评估。在对检测数据进行预处理之后，计算前文提出的6个评估指标。该里程原始不平顺样本的各特征量幅值大小统计结果见图1。

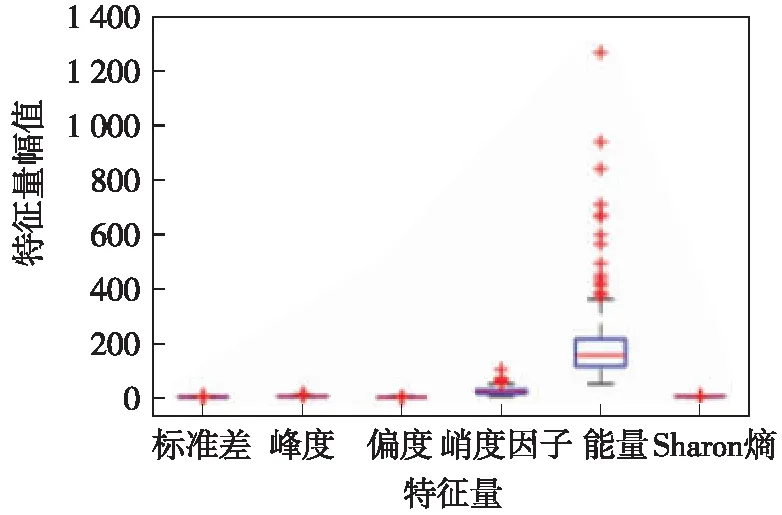
图1 基于统计箱型图的不平顺特征量结果

从图1可以清晰直观地了解到，各区段检测数据的多个特征量分布情况明显不同，说明此方法可以从多重维度反映轨道不平顺数据所携带的信息。

以正态分布为参照，就一般而言，各指标所能反映的物理意义如下：标准差大、峰度高可以反映出轨道不平顺中可能存在较多的极端值，峭度因子越小其概率密度曲线越平缓，可认为此种情况下的轨道不平顺分布情况越差；偏度小于0，称分布具有负偏离，也称左偏态，因为有少数变量值很小，使曲线左侧尾部拖得很长，直观表现为左边的尾部相对于右边的尾部要长；偏度大于0，称分布具有正偏离，也称右偏态，因为有少数变量值很大，使曲线右侧尾部拖得很长，直观表现为右边的尾部相对于左边的尾部要长，可认为当区段的偏度绝对值越大，此种情况下该区段轨道不平顺越可能存在极端值；能量能反映振动信号的幅值大小，可认为能量值越大该区段轨道不平顺更容易出现较大幅值；Sharon熵越大表示信号包含的信息量越大，信息的不确定性越大。结合各指标所代表的信号分布规律，管理时标准差、峰度、偏度、能量、Sharon熵等特征量应有对应的上限，峭度因子应有对应的下限。若某区段该特征量超出所对应的限值时，代表轨道不平顺分布状况越不服从理想状态的正态分布。由于新引入的指标阈值没有现有的规范或者文献以供参考，本文设定概率置信度为99%时的百分比阈值作为管理标准。结果统计见表3。

表3 概率置信度为99%对应的百分比阈值

根据表3的阈值，标定各指标的超限区段以加粗点展示，由于各指标数值差异较大，为了便于比较，采用双纵坐标展示各特征量幅值分布结果，见图2。

图2 多个特征量分布情况

观察图2，以现有评价指标即标准差为例，统计结果表明：没有任何区段超过现有规范标准差限1.5；但若以其他特征量为标准，某些区段存在不同的超限情况。为了进一步分析现有评价方法的不足，将这些由多指标确定的所有超限区段共8个由小到大排序作为工况1，并在该里程其他所有特征量均未超标的区段中任意选择8个区段作为工况2，两种工况不平顺样本见图3。

图3 两种工况不平顺幅值分布情况

由图3可知，工况1不平顺幅值明显大于工况2，且前者波形图有较多的毛刺现象，即工况1可能存在较强的局部波动现象。分别从峰值法、轨道质量指数两种方法进行对比分析，工况1与工况2不平顺幅值均满足I级保养标准，线路状态良好；工况1不平顺的标准差的值均大于工况2不平顺的标准差值，但两者均未超过现有高低不平顺单项标准差的管理阈值。

3.2 动力学仿真和时频分析验证

为了进一步研究两种工况下的轨道实际状态，利用SIMPACK多体动力学软件，建立具有42个自由度的车辆模型，车辆模型的主要参数参考文献[20]，车辆的运行速度设定为200 km/h， 可得到两种高低不平顺工况激励下的动力响应，见图4。

图4 两种高低不平顺工况激励下的动力响应

由图4可知，在两种高低不平顺工况影响下，车体振动加速度远小于《高速动车组整车试验规范》中的限值;在788 m里程处，工况1的轮轨垂向力出现极大值与极小值，此时轮重减载率1，远远超过规范中限值0.65，此处轮轨间可能存在非常大的相互作用力，造成轨道和机车车辆部件损坏，甚至危及行车安全，工务部门应对该里程处进行重点监测管理。工况1788 m里程处不平顺小于250 m里程处的幅值，但前者动力学响应指标却远远高于后者，这也说明现有的评价方法不能反映轨道的真实状态。为了进一步挖掘轨道实际状态，对两种工况下高低不平顺进行时频分析，如图5所示。

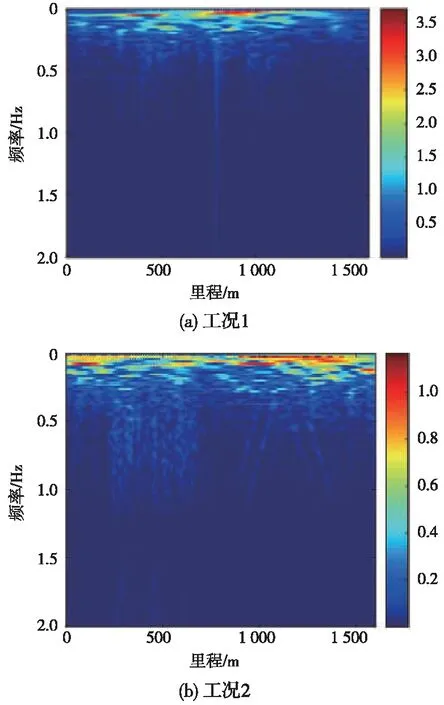
图5 两种工况下高低不平顺时频分析

由图5(b)知，工况2能量较小且分布均匀，没有存在明显的能量集中现象，表明此时钢轨状态较好；由图5(a)可知，工况1分别在里程400 m处存在波长为14～18 m的能量集中和里程788 m至900 m附近出现波长20～33 m的能量集中，可认为此处钢轨可能存在某种病害造成了短波不平顺能量集中，需要重点检修维护，本文旨在说明利用多个特征量综合评估轨道状态的必要性，故不对具体病害形式继续探讨。

4 结论

在结合现有轨道不平顺评估方法的研究基础上，提出一种基于多个时域特征量的轨道状态综合评估方法。利用采集的大量轨检数据，统计其多个特征参数，并用主成分分析法对数据进行降维处理，基于概率置信度确定可能存在病害的轨道位置，再由动力学仿真观察病害处的动力响应特性。可以得到如下结论。

(1)同一位置处的不同特征量指标的超限情况不同，仅由轨道质量指数诊断轨道状态，可能会造成实际状态的误判，结合多个特征量可以更全面的挖掘不平顺数据所包含的信息。

(2)主成分分析法在极大程度上浓缩了原始数据所包含的有用信息，可以更快速有效实时地分析轨道状态。

(3)结合动力学仿真和时频分析结果可知，里程788 m处，两种工况的幅值分布情况与单项轨道质量指数并没有显著差别，但工况1在该处轮轨垂向力出现极值和轮重减载率接近1，远远超出规范标准；工况1不同里程处出现了某波长范围的能量集中，应在该里程处对可能造成此种短波不平顺的轨道病害进行重点检测。

综上，利用实测轨道不平顺数据分析发现，主成分分析法有助于快速精简地获得轨检数据所包含的轨道状态信息，结合轨道质量指数与多个时域特征量，可以找到可能存在潜在病害的轨道位置，对该处进行动力学仿真和时频分析，可以仅从数据角度初步确定该里程处可能存在的病害，有利于该里程处的重点监测与养护维修。该方法为轨道状态的诊断提供一种新思路，有助于更加全面科学地评估轨道状态，节约监测成本，对工务部门管理轨道的养护维修具有重要意义。