与小学生漫话圆周率
2020-05-18安徽省安庆市岳西县实验小学储银桃
安徽省安庆市岳西县实验小学 储银桃
在小学六年级开始学习圆的知识,如圆的周长计算公式C=2πR,圆的面积计算公式S=πR2。这其中,圆周率π是一个相当重要的数学常数,这个常数在后续的数学课程中如影随形,如三角函数、立体几何、概率统计中都能见到它的身影;在其他自然科学中也随处可见,如物理中单摆的周期公式、海森堡的不确定性原理、爱因斯坦相对论的场方程等。可以说,π的历史,涉及人类文明包括数学学科的整个发展历史。适度地给小学生深入浅出地讲解这个常数,介绍它的神奇性质、它的前世今生,可以激发小学生学习数学的兴趣和勇攀科学高峰的精神;给小学生讲解中国古代数学家在这方面所做出的杰出贡献,对激发学生的爱国热情和民族自豪感也有重要意义。
一、圆周率的定义、性质及早期近似值
在人类从事生产生活过程中,大自然中最早引起人们注意的几何图形大概就是圆了,天上的太阳和满月、一些植物的花朵(如向日葵等)、平静水面上漾起的一圈圈涟漪都给人以圆的形象。圆具有高度的对称性,过圆心的任何一条直线都是其对称轴,圆周上任意一点到圆心的距离都相等。或许经过了一个漫长的时期,人们认识到所有的圆都是相似的,任意一个圆的周长C 与其直径D 之比为一个固定不变的数——数学上称为常数,这个常数就是圆周率。1737 年,大数学家欧拉采用希腊字母π 来表示这个常数,自此,π 便成为表示圆周率的通用记号。
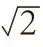
如果知道了圆周率π 的数值,可以由圆的直径计算出圆的周长或面积,圆周率π 数值越精确,计算结果就越精确。在人类文明的早期,人们就是取它的有限位近似值用于工农业生产中的计算。根据最早有文字的记载,在公元前2000 年前后,巴比伦人取π 的近似值为3.125,埃及人则采用3.1605,我们国家在公元前1200 年的周朝使用3 作为π 的近似值,并一直使用了好几个世纪,这就是《周髀算经》所记载的“圆径一而周三”,即“圆的直径为1,则周长为3”,与世界其他各国同期相比,这算不上一个先进的纪录。到了130 年,在《后汉书》中采用3.1622 作为近似值,比3精度要高一些。至于另一四大文明古国——印度,在400 年前后,开始采用3.1416 作为近似值,这已经具有很高的精度,在绝大多数场合用它做计算已经足够了。
二、圆周率的计算方法
人类在早期所采用的圆周率的近似值估计是通过测量和经验得到的,这类获取圆周率近似值的方法对精度的提高是有限的,例如,假设我们采用有毫米刻度的软尺来测量一个直径为1 米的圆的周长和直径,由于测量总会有误差,毫米以下要靠测量者进行估计,直径可能读为1.0003 米,周长可能读为3.1396 米,这样计算出来的圆周率近似值就是3.1386584,小数点后第2 位就开始不准确了。因此,探求一种可以将圆周率的数值能计算到任意精度的方法就变得很重要了,古希腊数学家、物理学家阿基米德和我国古代数学家刘徽、祖冲之在这方面做出了杰出贡献。
(一)阿基米德方法
到了公元前3 世纪,古希腊最伟大的数学家、物理学家阿基米德(前287—前212)首次提出了可以将π 的数值计算到任意精度的一般性的方法。他的方法的根据是:圆内接正多边形的周长比圆周长小,而圆外切正多边形的周长比圆周长大,将圆内接正多边形及圆外切正多边形的边数不断加倍,它们就愈来愈接近圆周了。
具体而言,阿基米德从单位圆出发,先用内接正六边形周长求出圆周率的下界为3,再用外切正六边形周长并借助勾股定理求出圆周率的上界为4。接着,他对内接正六边形和外切正六边形的边数分别加倍,将它们分别变成内接正12 边形和外切正12边形,再借助勾股定理改进圆周率的下界和上界。他逐步对内接正多边形和外切正多边形的边数加倍,经过四次加倍后,得到内接正96 边形和外切正96 边形。最后,他求出圆周率的下界和上界后再取它们的平均值,得到圆周率的近似值:3.141851。
(二)刘徽与割圆术
生于三国时代魏国的刘徽,在对中国古代算经《九章算术》作注时,于264 年也提出了与阿基米德相类似的方法,刘徽将该方法命名为割圆术。与阿基米德类似,刘徽也是取半径为1 的单位圆,开始时作圆内接正六边形和圆外切正六边形,但与阿基米德不同的是,刘徽不是计算它们的周长,而是计算它们的面积,从图1 更容易直观地看出,圆的面积必定介于圆内接正多边形面积和圆外切正多边形面积之间。边数不断倍增,从6 到12 再到24、48、96、192,直至3072。
他在书中写道:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。这段朴素精练的语言蕴含着极限的思想,说明了内接正多边形随着边数不断倍增,其面积无限接近于圆的面积。刘徽将正多边形边数倍增到192 时,求得3.141024<π<3.142704,边数倍增至3072 时,求得π≈3.14159。
刘徽不仅得到了相当精确的π 的近似值,而且提出了一个可以计算π值到任意精度的一般性的方法,这虽然已在阿基米德之后的500 多年了,但处于当时的条件,交通和通信极其落后,刘徽不可能知道阿基米德的方法,因此,刘徽的割圆术应该被视为他自己的原创性工作。

图1 刘徽割圆术:边数从6 培增至12 倍
无论是阿基米德方法,还是刘徽的割圆术,都涉及勾股定理及开方运算,这都超出了小学生的知识范围,因此只需讲解算法基本思想,具体计算过程从略。
(三)祖冲之的约率、密率
讲到中国学者对圆周率的贡献,不能不提祖冲之。祖冲之是南北朝人,在5 世纪时可能采用了刘徽的割圆术,将π 的数值计算到3.1415926<π <3.1415927,即精确到小数点后第七位,这是非常了不起的成就,欧洲直到16 世纪才取得如此高精度的值,祖冲之的计算结果领先了欧洲足足11 个世纪。
祖冲之对圆周率的贡献,特别使人吃惊和感兴趣的是他找到了两个简单易记的分数来近似表示圆周率,即密率
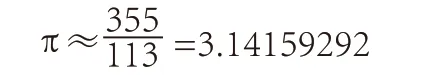
和约率
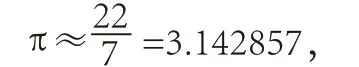
在分母小于100 的分数中,约率22/7 是最接近π 的分数;在分母小于30000 的分数中,密率355/113 是最接近π 的分数。尤其是密率,精度很高又容易记忆,这个结果直到1573 年才为德国人奥托(V.Otho)重新发现,但这已经是1000 多年以后的事了。
三、有关π 的其他趣事
圆周率π 是如此神奇,以至于人们对它宠爱有加。在法国巴黎的发现宫中,专门有一个关于π 的大厅,厅门上方印有含有π 的欧拉公式,厅内墙壁上则印着π 的精确到小数点后707 位的数值。世界各地的圆周率爱好者还根据圆周率的前三位数字3.14确定每年3 月14 日为“π 日”,他们在那天聚会,讨论有关π 的话题,吃以馅饼为主的美食——因为馅饼的英文pie 发音与π 相同,并互祝“π 日快乐”。
关于π 的计算,前文中介绍了阿基米德方法、刘徽的割圆术、祖冲之的约率和密率等,此外,还有其他高等数学的方法,如积分方法、级数方法,这些都是确定性方法。1777 年,法国科学家蒲丰(Buffon)提出了投针实验方法计算π,他首次使用随机实验处理确定性数学问题。具体做法是这样的,在平地上画很多距离相等的平行线,随机地向地上投掷一根针,针的长度小于平行线间的距离,这样,针要么与平行线不相交,要么与其中某一条平行线相交,重复很多次,统计针与平行线相交的次数,列一个方程,就能计算出π 的近似值,是不是很神奇?当然,这种方法无法控制π的精确度,实验次数增多并不意味着精度就会提高。但这种方法引申出当今一个重要的计算方法,即以赌城蒙特卡罗(Monte Carlo)命名的蒙特卡罗方法。
从人类对圆周率π 的认识不断深化的历史,可以看到科学是永远充满活力并不断开拓前进的。作为小学生,要从小就立志发奋学习、献身科学、报效祖国、为全人类谋幸福。中国古代数学家在当时极其低下的条件下,做出了世界领先的研究成果,这种探索和钻研精神也需要我们学生继续传承下去。
